动态规划算法详解：从矩阵连乘到资源分配

"该资源是关于《算法分析与设计》课程的第四讲，主题是动态规划。课程内容包括动态规划的基本要素，通过多个例子来阐述动态规划的应用，如矩阵连乘问题、凸多边形最优三角剖分、最长公共子序列、多段图的最短路径问题、0-1背包问题以及资源分配问题。动态规划是一种解决子问题之间存在依赖关系的方法，通过存储子问题的解来避免重复计算，从而提高效率。课程介绍了动态规划的基本步骤，包括确定最优解的性质、递归定义最优值、自底向上计算最优值以及构造最优解。此外，还特别讨论了矩阵连乘问题，分析了枚举法解决此类问题的时间复杂度。" 在算法分析与设计中，动态规划是一种重要的解决问题的方法，它与分治法相似，但处理的问题子集通常不是相互独立的。当使用分治法时，可能会出现子问题被重复计算的情况，而动态规划通过存储子问题的解来避免这种情况，从而实现更高效的算法。 动态规划的基本步骤分为四步： 1. 描述最优解的性质：这一步需要识别问题的结构特性，确定哪些特征是构成最优解的关键。 2. 递归定义最优值：对每个子问题，定义一个函数来表示其最优解的价值。 3. 自底向上的计算：从最小规模的子问题开始，逐步计算较大规模子问题的最优值，构建一个表格存储这些值，这个过程称为填表。 4. 构造最优解：通过之前计算的表格，反向推导出整个问题的最优解。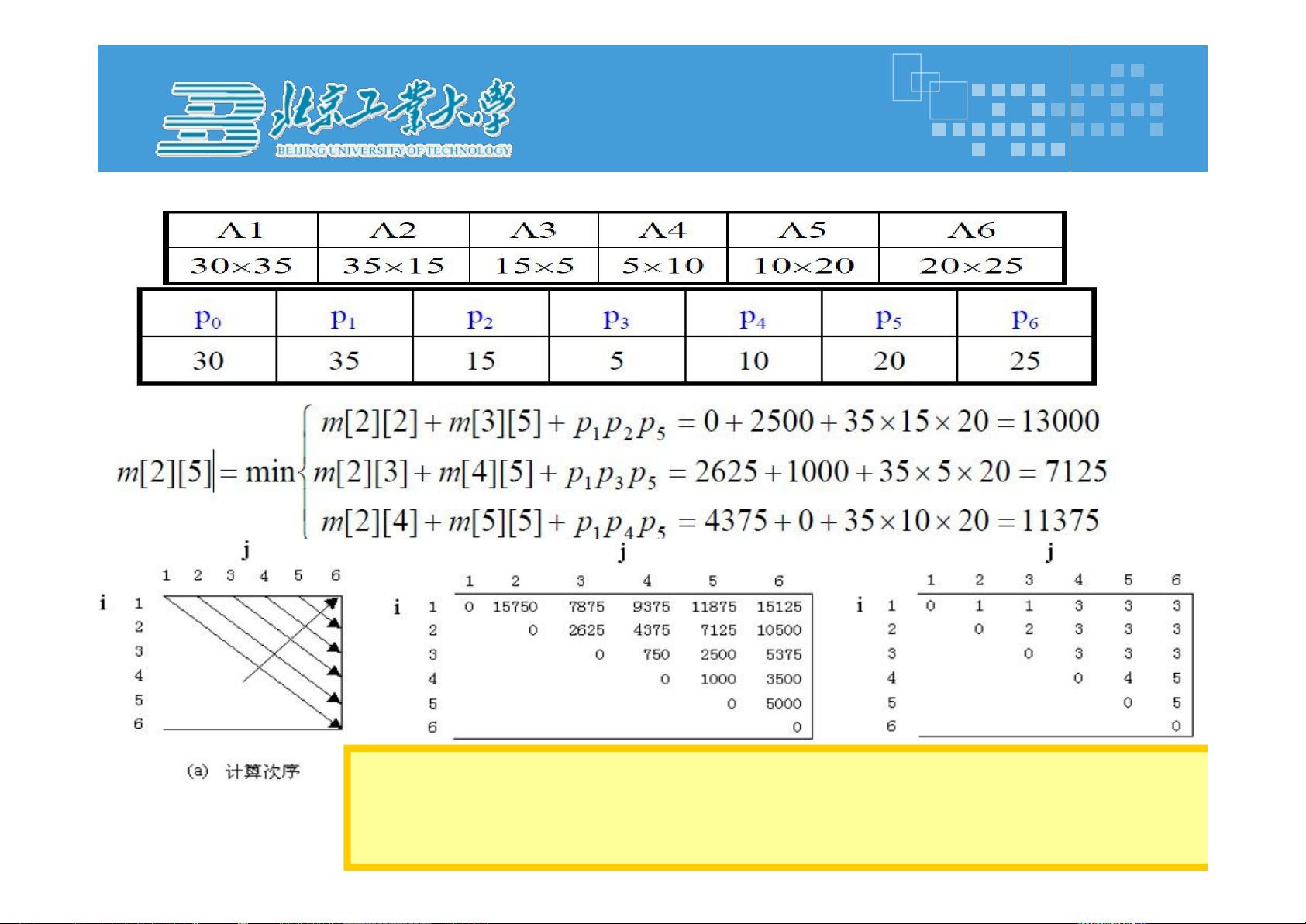 课程中举了多个动态规划应用的例子，例如： - **矩阵连乘问题**：寻找计算矩阵乘积的最优次序，以最小化所需的乘法次数。枚举法虽然直观，但时间复杂度高，不适合大规模问题。 - **凸多边形最优三角剖分**：如何将一个多边形划分为最少数量的三角形，使这些三角形都是凸的。 - **最长公共子序列**：在两个序列中找到最长的子序列，该子序列在原序列中都存在，但不必连续。 - **多段图的最短路径问题**：在包含多个起点和终点的图中，寻找总距离最短的路径。 - **0-1背包问题**：给定物品的重量和价值，确定如何选择物品放入容量有限的背包，以最大化总价值。 - **资源分配问题**：如何合理分配有限的资源以达到最佳效果。 通过这些例子，学习者可以深入理解动态规划的概念，掌握其应用和优化策略，提升解决复杂问题的能力。