递归与回溯：经典算法与面试挑战

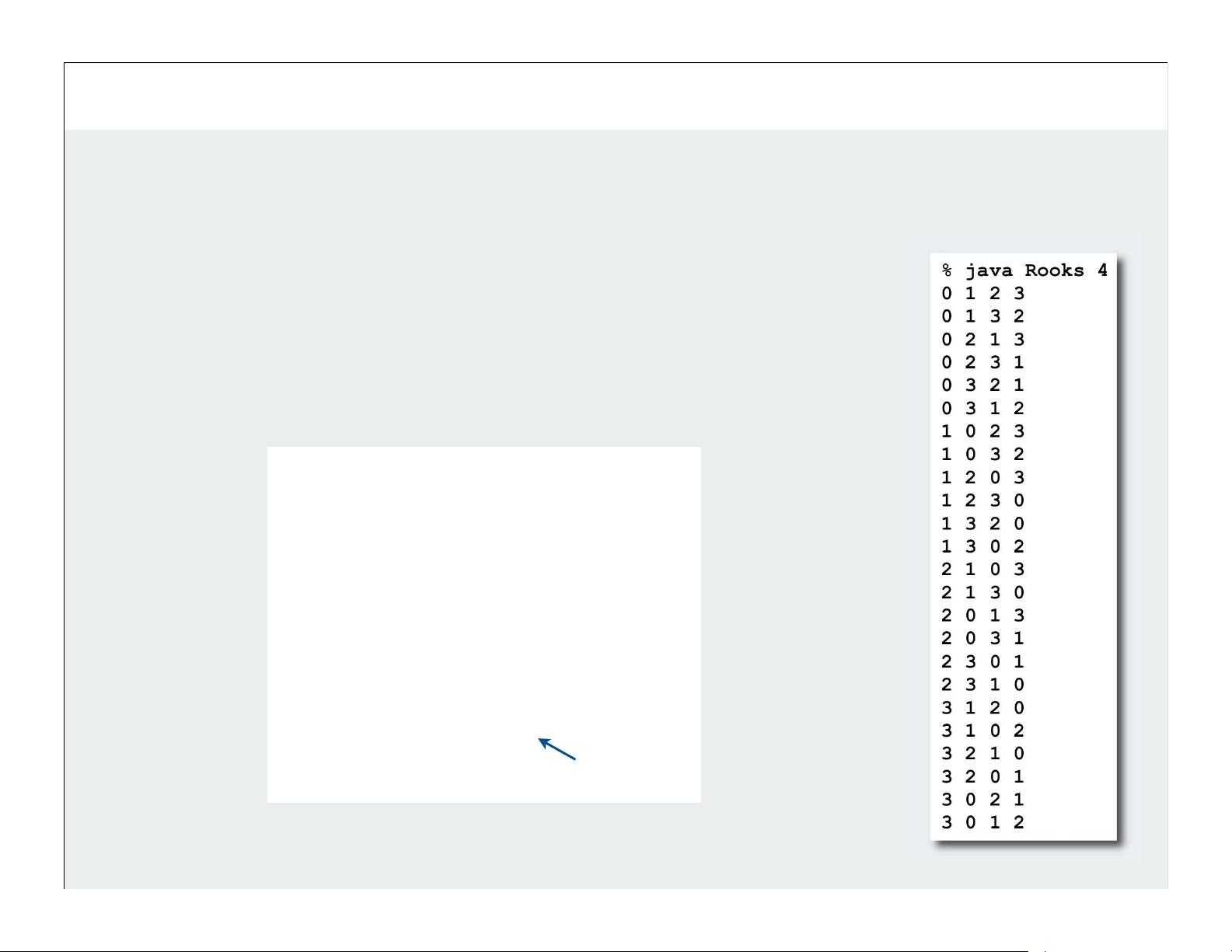
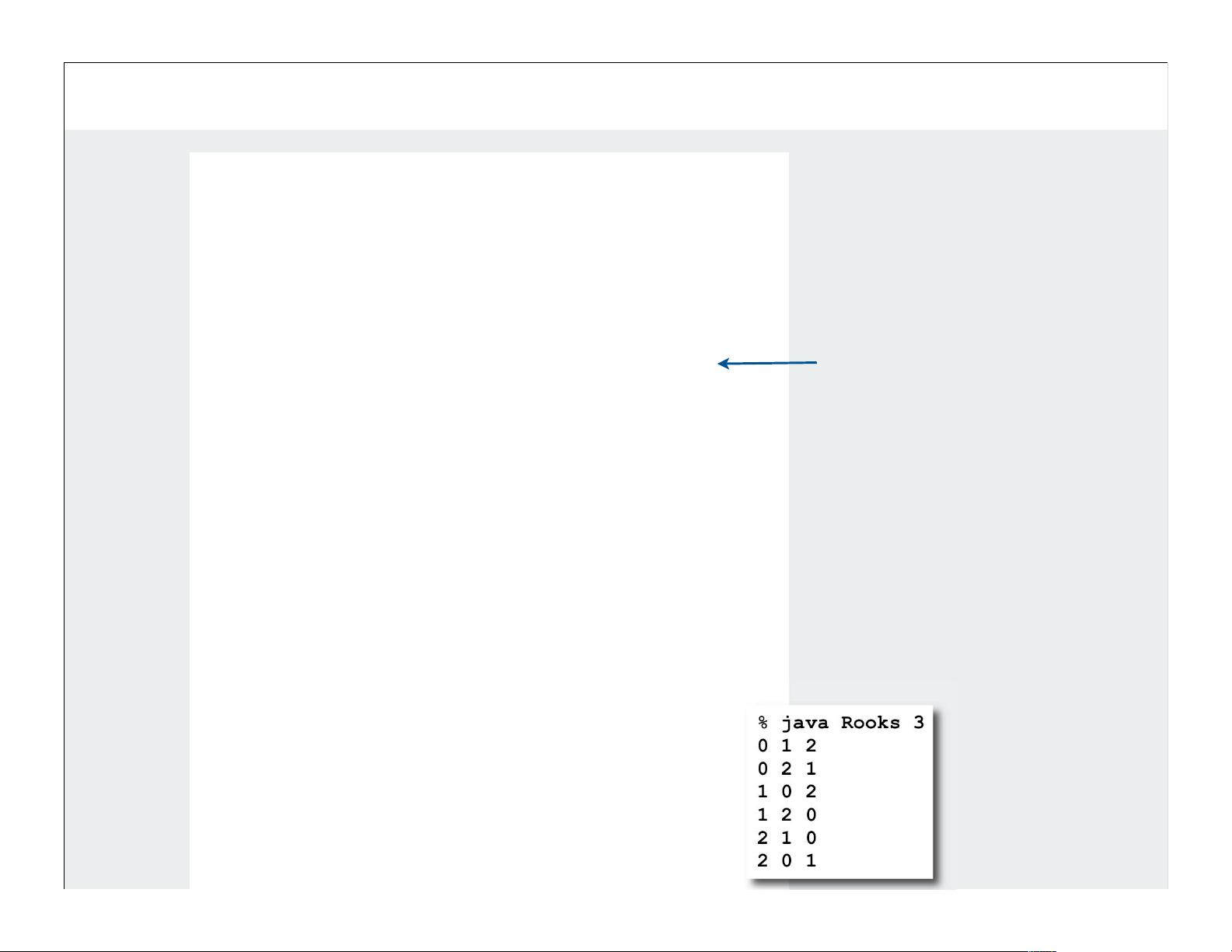
在IT领域，递归（Recursion）和回溯法（Backtracking）是两种强大的算法工具，它们常用于解决组合搜索、排列、计数、子集以及图中路径等复杂问题。这两者在许多经典编程面试中都是考察重点，尤其对于像普林斯顿等顶级学府的计算机科学课程来说，它们是理解和应用核心算法的关键。 **1. 回溯搜索（Backtracking）：** 回溯法是一种策略，通过系统地检查所有可能的解决方案来寻找问题的解答。这种方法适用于那些可能有大量潜在解决方案但并非所有方案都可行的问题，例如在所有可能的N位二进制字符串中找到满足特定条件的组合。当搜索空间通常是指数级增长时，回溯能够有效地缩小范围，即使面对相对较大的问题实例也能保持效率。 例如，一个经典的warm-up问题是枚举所有的N位二进制字符串，这等同于从0到\(2^N-1\)进行二进制计数。通过递归方法，我们可以维护一个数组a[i]，初始化为0，然后调用enumerate函数： ```java private void enumerate(int k) { if (k == N) { process(); // 处理当前的N位字符串 return; } enumerate(k + 1); // 递归处理下一个位置 a[k] = 1; // 设置第k位为1 enumerate(k + 1); // 再次递归处理，这次设置第k位为0 // 在递归结束后，执行清理操作 } // 清理函数，确保正确结束所有可能路径 public void cleanup() { // 开始时所有位都是0 for (int i = 0; i < N; i++) { // 清除之前设置的所有值 a[i] = 0; } } ``` **2. 递归（Recursion）：** 递归是将一个问题分解为规模较小的相同或类似问题，并通过解决这些子问题来求解原问题的方法。在上述二进制字符串枚举问题中，递归的运用体现在`enumerate`函数中，通过保持不变量（证明为归纳推理的基础），确保所有N-k位字符串都被正确枚举并最终返回结果。 **应用范围与限制：** 虽然回溯和递归能处理广泛的难题，包括NP完全问题，但其效率受到搜索空间大小的影响。在大规模问题上，如果没有有效的剪枝策略，可能导致性能瓶颈。然而，通过巧妙设计，回溯可以减少搜索空间的大小，使得算法在实际应用中仍然可行。 总结，递归和回溯是IT领域解决复杂问题的强大工具，掌握它们有助于理解并解决诸如排列、组合、计数和路径查找等问题。在面试中，熟练掌握这些算法的原理、示例和优化策略将有助于提升求职者的竞争力。