理解栈的LIFO特性：通过Python解题

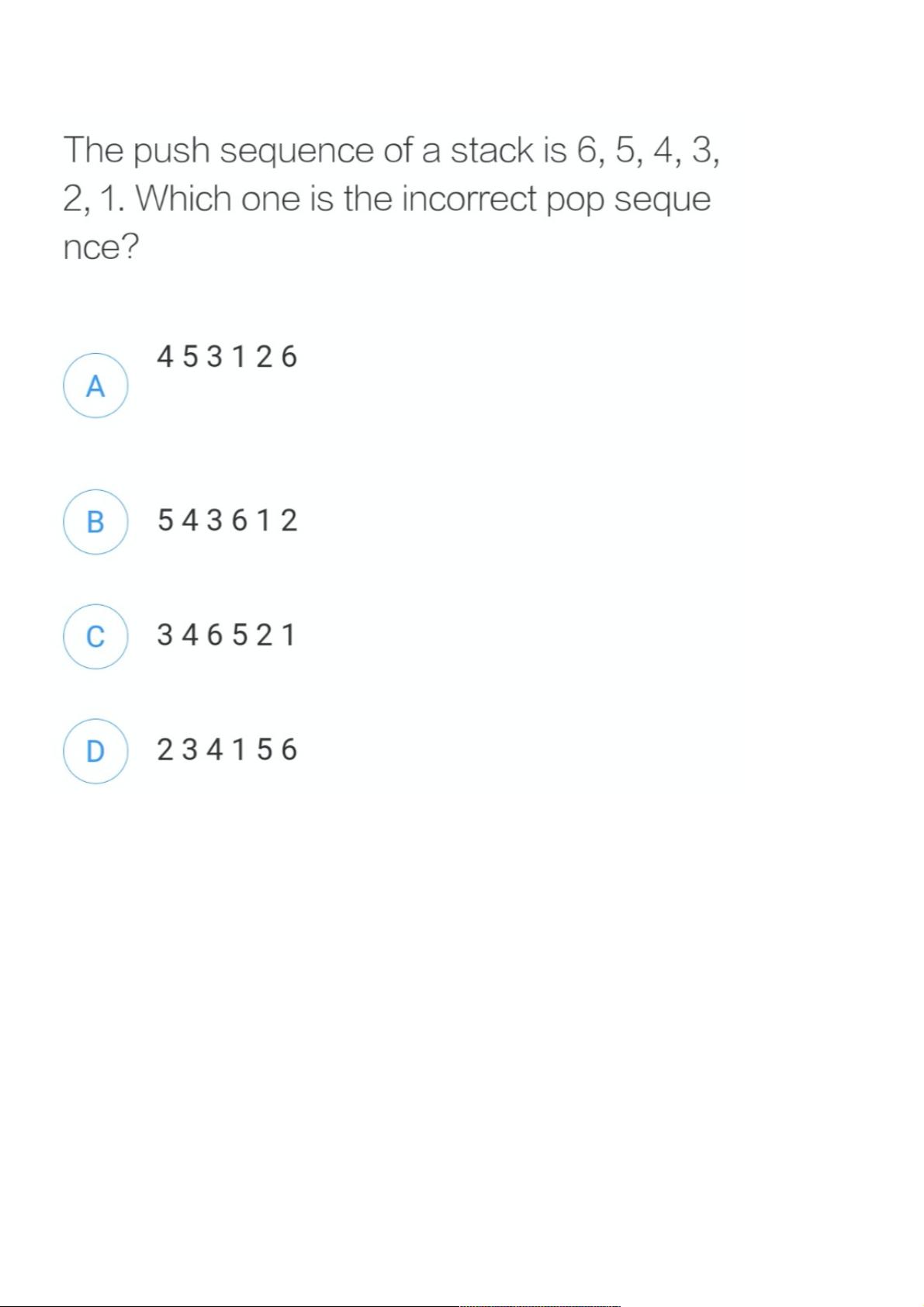
"本文主要通过一道关于栈的题目来深入理解栈的后进先出（LIFO）原理，以及如何用Python实现相关操作。题目要求根据给定的初始栈序列654321，判断一系列操作后是否能得到特定序列。" 在计算机科学中，栈是一种特殊的线性数据结构，其特点是遵循“后进先出”（Last In, First Out，简称LIFO）的原则。当元素被添加到栈中时，它们被称为被“压栈”（push），而当需要访问或移除元素时，总是从栈顶开始，这一过程称为“出栈”（pop）。栈在许多算法和编程问题中都有应用，如括号匹配、深度优先搜索等。 题目描述的解题思路如下： 1. 给定一个初始栈序列，例如654321，我们需要判断是否可以通过一系列的push和pop操作，得到另一个特定的序列，例如453126。 2. 从特定序列的第一个元素开始，检查栈顶元素是否匹配。如果匹配，则执行pop操作；如果不匹配，则需要从辅助栈st_tmp中寻找匹配的元素，并将其按LIFO顺序转移到主栈st中。 3. 如果在辅助栈st_tmp中找不到匹配的元素，那么该特定序列不可能通过push和pop操作得到，因此序列不正确。 4. 最终，如果所有元素都被正确处理，且两个栈都为空，那么特定序列是可以通过初始栈序列得到的。 为了实现这个解题思路，我们可以创建一个简单的栈类`SStack`，它使用Python的列表作为底层数据结构。这个类包括`is_empty`方法来检查栈是否为空，`top`方法来获取栈顶元素，以及`push`和`pop`方法来执行压栈和出栈操作。此外，还可以定义一个自定义异常类`StackUnderflow`来处理栈空时尝试出栈的情况。 以下是可能的Python代码实现： ```python class StackUnderflow(ValueError): pass class SStack: def __init__(self): self._elems = [] def is_empty(self): return self._elems == [] def top(self): if self.is_empty(): raise StackUnderflow("Stack is empty") return self._elems[-1] def push(self, item): self._elems.append(item) def pop(self): if self.is_empty(): raise StackUnderflow("Stack is empty") return self._elems.pop() # 其他辅助方法，如print_stack等，用于调试和查看栈的状态 ``` 通过这样的数据结构和操作，我们可以编写一个函数来模拟题目中所述的序列判断过程。这个函数会遍历给定的序列，使用栈操作判断是否能得到目标序列。如果在遍历过程中遇到无法匹配的情况，或者在结束时仍有元素留在栈中，函数将返回False；否则，返回True。 理解和掌握栈的后进先出特性对于解决许多编程问题至关重要。通过实践题目中的方法，我们可以更好地掌握这一概念，并能够运用到实际编程中。