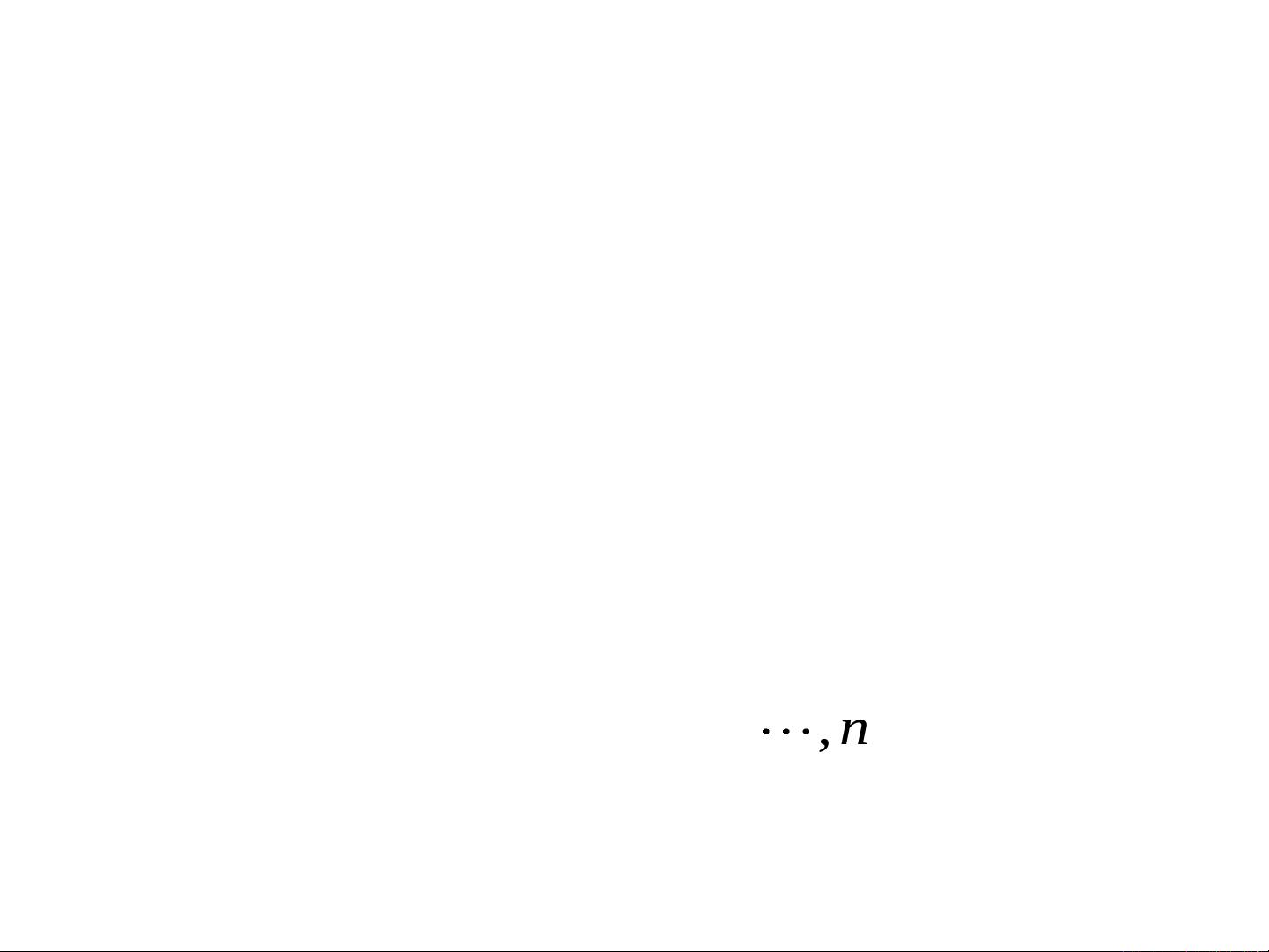一阶常微分方程数值解方法：欧拉法、龙格-库塔法

"该资源是一份关于数值分析的PPT，重点讲述了如何使用数值方法解决常微分方程。内容涵盖了欧拉法、龙格-库塔法、线性多步法以及一阶和高阶微分方程组的数值解法。在科学和工程领域，常微分方程经常出现，但由于解析解的困难性，数值解法显得尤为重要。本PPT还讨论了解的存在性和唯一性的条件，以及如何通过离散节点寻找方程的数值解。" 在数值分析中，常微分方程数值解法是关键内容。其中，8.1章节介绍了欧拉法，这是一种基础的数值积分方法，适用于简单的常微分方程初值问题。欧拉法通过有限的步长逐步逼近真实解，但其精度受到步长大小的直接影响。 8.2章节涉及龙格-库塔法，这是一种更高级的数值解法，包括多种不同的公式，如二阶的龙格-库塔方法（Heun's method）和四阶的Runge-Kutta方法。这些方法通过结合多个阶段的欧拉步骤来提高精度，同时保持稳定性的特性。 8.3章节提到了线性多步法，如亚当斯方法（Adams method）和巴塞利斯-布劳威尔方法（Bashforth-Brouwer method），它们利用前几步的解信息来预测下一步的近似值，从而提高效率和准确性。 8.4章节探讨了一阶微分方程组和高阶微分方程的数值解法，这些问题在实际应用中更为复杂。对于一阶微分方程组，可以将每个方程视为独立的欧拉法或龙格-库塔法的应用，而高阶微分方程通常需要降阶处理，转化为一阶系统再进行数值求解。 在数值解法中，解的存在性和唯一性至关重要。定理8.1阐述了李普希茨条件，这是保证解存在的关键，它要求函数f在指定区间内连续并且满足一定的有界性。如果函数满足这个条件，那么初值问题就有唯一解。在实际应用中，如果函数有连续偏导数，这通常可以作为李普希茨条件的替代。 数值解法的基本思想是将连续的自变量x空间离散化，得到一系列的节点x_i，并在这些节点上近似求解。通过逐步推进，从已知的初始条件出发，计算出每个节点处的解y_i。这种方法被称为初值问题的数值解。步长h的选择对解的精度有很大影响，通常会选择较小的步长以提高精度，但过小的步长会导致计算量过大。 这份PPT详细讲解了常微分方程数值解法的基础理论和常见方法，为理解和应用数值解法提供了扎实的基础。