遗传算法应用:MATLAB实现一元函数优化
版权申诉
61 浏览量
更新于2024-07-03
收藏 1.86MB PDF 举报
刚刚的回答出现了一些中断,现在我将继续完成内容。
SelCh=mutate('scram',SelCh,0.03);
%变异
Chrom=SelCh;
gen=gen+1;
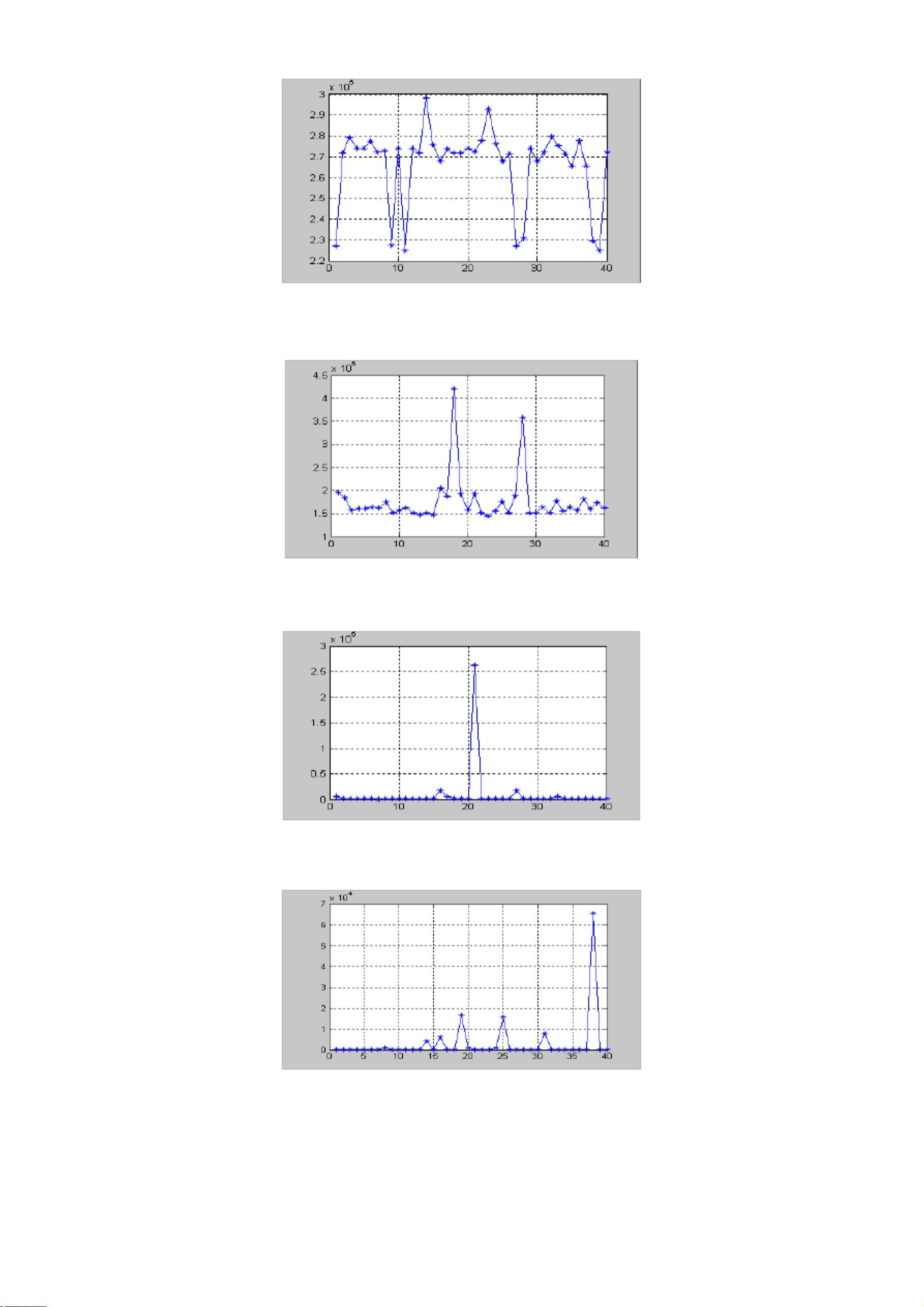
trace(1,gen)=mean(ObjV);
%记录当前代的平均目标函数值
variable=bs2rv(Chrom,FieldD);
%计算新种群的十进制转换
ObjV=variable.*sin(10*pi*variable)+2.0;
%计算新种群的目标函数值
end
%最佳个体的寻找
[~,index]=min(ObjV);
bestSol=variable(index,:);
%绘制优化过程
figure(2);
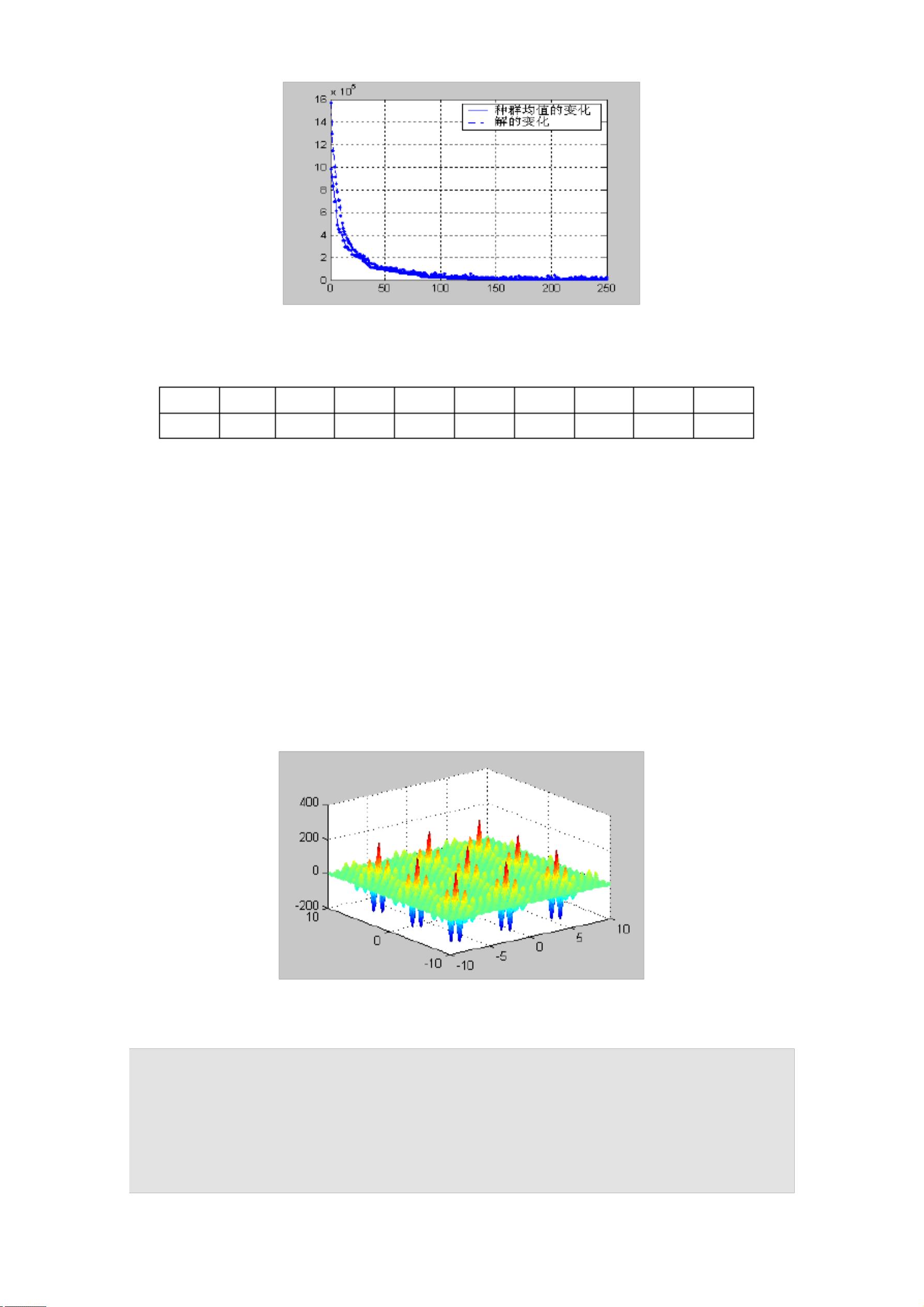
plot(1:MAXGEN,trace);
xlabel('Generation');
ylabel('Objective Function Value');
title('Optimization Process');
7.2旅行商问题(TSP)实例
旅行商问题是一个经典的组合优化问题,目标是找到访问一系列城市并返回起点的最短路径,每个城市只访问一次。以下是一个使用遗传算法求解TSP的MATLAB实现简化版的例子。
首先,生成随机城市坐标,然后定义遗传算法参数,如种群大小、最大迭代次数等。接着,编码城市顺序为二进制串,进行初始化种群。遗传算法的主要步骤包括适应度分配、选择、交叉和变异。最后,找到具有最小路径长度的个体作为解决方案。
这个例子中,遗传算法的核心在于如何将城市顺序转化为适应度值,并设计合适的交叉和变异操作以保持解的合法性。在实际应用中,可能还需要引入精英保留策略以避免最优解的丢失。
通过这两个实例,我们可以看出遗传算法在解决实际问题中的灵活性和有效性。它不仅能在一元函数优化问题中找到全局最优解,还能处理像旅行商问题这样复杂的组合优化问题。在实际工程中,遗传算法常常被用来解决各种优化挑战,尤其是在问题规模庞大、传统方法难以求解的情况下。然而,遗传算法也有其局限性,例如收敛速度较慢,需要调整的参数较多,以及可能陷入局部最优等。因此,在实际应用中,需要根据具体问题选择合适的算法参数,并结合其他优化技术,如模拟退火、粒子群优化等,以提高求解效率和精度。
点击了解资源详情
点击了解资源详情
点击了解资源详情
118 浏览量
2021-12-17 上传
671 浏览量
637 浏览量
906 浏览量
点击了解资源详情
G11176593
- 粉丝: 6927
- 资源: 3万+
最新资源
- vip会员统计表excel模版下载
- containerBooking
- like-me
- node-async-await-example:具有异步等待用法的Node.js应用程序的简单示例
- F460dll_for_TOT_KLS.rar
- NRRD 格式文件阅读器:NRRD 文件阅读器-matlab开发
- upptime:Up Upptime的正常运行时间监视器和状态页面,由@upptime提供支持
- 幼儿园财务报表excel模版下载
- Calculator:在Android Studio上使用Kotlin的基本计算器
- luckytuan-fast-loader-master.zip
- adc-analysis:SciCRT的跟踪分析
- SCANProject:堆叠式交叉注意项目页面
- 公司会议室3D模型
- pushNaNs:将 NaN 推送到 X 的每一列的底部。-matlab开发
- ManuelGil:个人资料
- 爱普生(Epson)L805 原版清零软件