清华大学出版社《数据结构》第六章：图论与欧拉回路详解

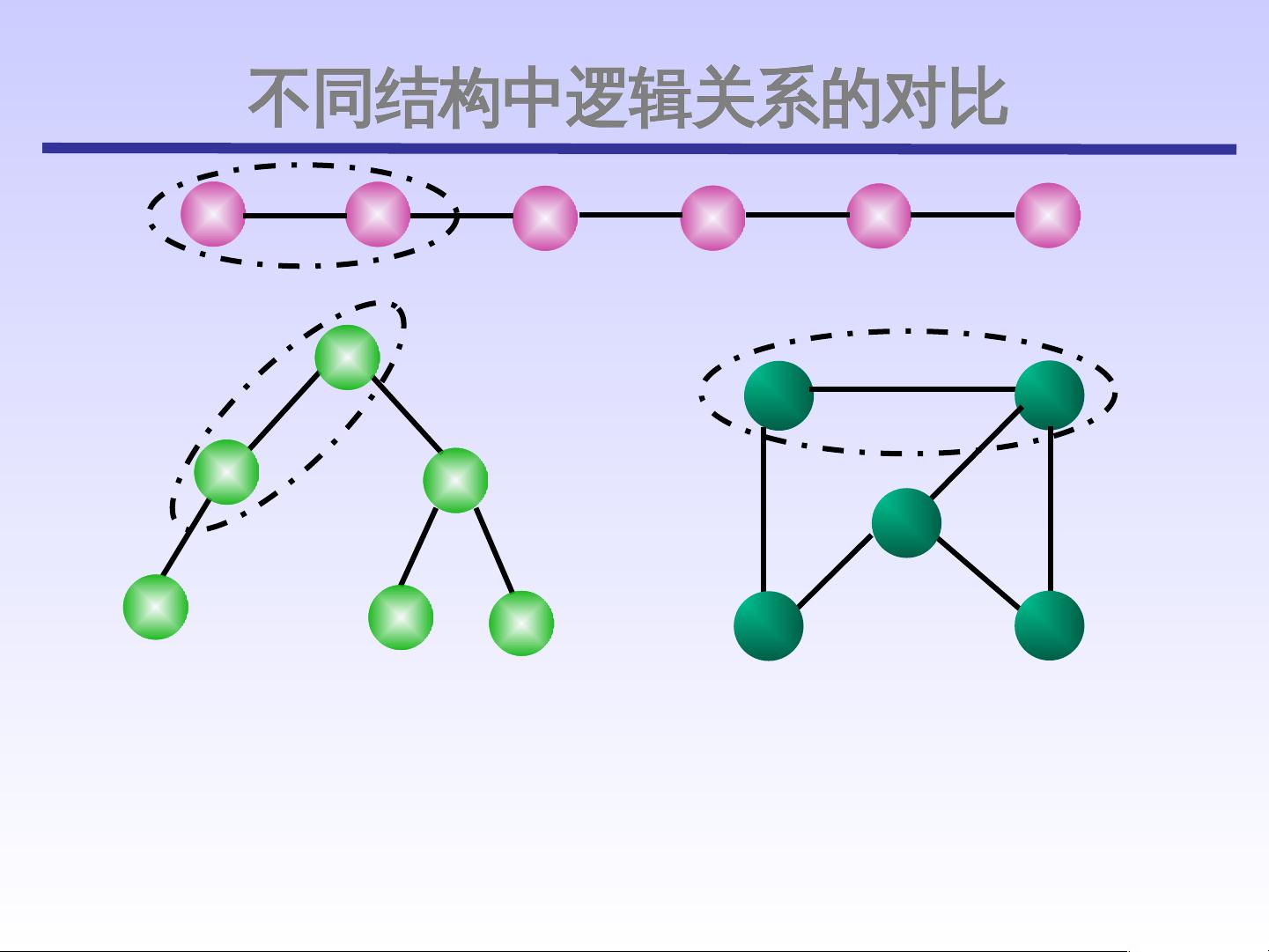
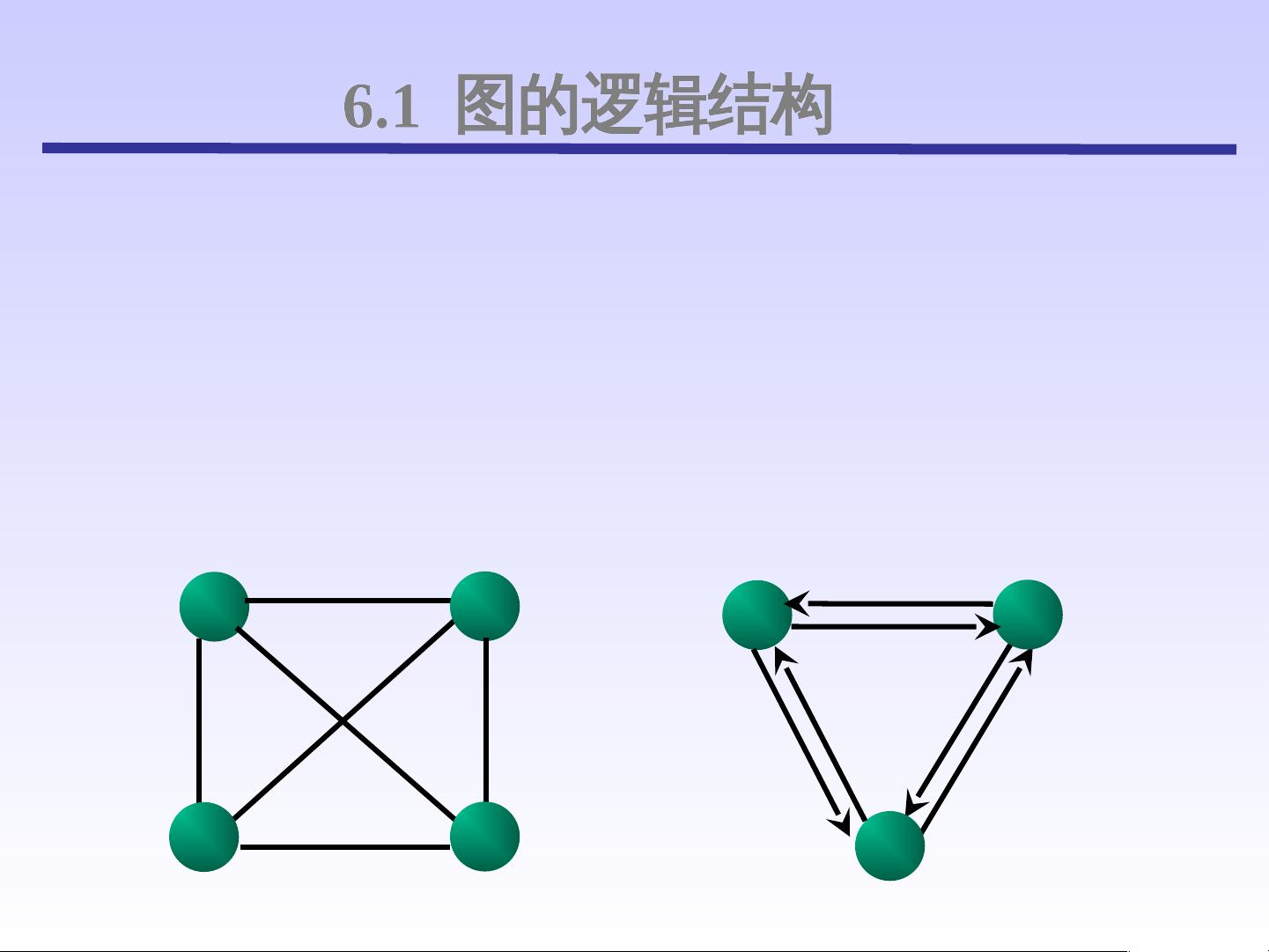
本章节来自《数据结构（C++版）》一书，由清华大学出版社出版，专注于图论这一重要概念在计算机科学中的应用。第六章名为“图”，是数据结构课程中的核心内容，它涵盖了图的基本概念、逻辑结构和存储结构。 首先，图的逻辑结构是本章的基础，图被定义为由顶点的有穷非空集合V和顶点间边的集合E组成，通常用符号G=(V,E)表示。区别在于，线性表和树中元素或节点数量可以为零（为空），而图中至少需要有一个顶点，但边的数量可以是任意的。图还可以进一步分为无向图和有向图，无向图中任意两个顶点之间的边无方向性，用(vi,vj)表示；而有向图则有明确的方向，如<vi,vj>。 图的存储结构和其实现是接下来的重点，这部分探讨如何在计算机内存中有效地组织和管理图的数据结构，包括邻接矩阵、邻接表等常见方法。这些数据结构的选择会影响算法的时间复杂性和空间效率。 接着，本章深入讲解了图论中的两个核心概念：最小生成树和最短路径。最小生成树是图中连接所有顶点的边的最小集合，通常通过Prim算法或Kruskal算法来求解。而最短路径问题涉及寻找图中两点间的最短路径，Dijkstra算法和Floyd-Warshall算法是解决此问题的经典方法。 此外，章节还讨论了网络流问题，如AOV网（活动-对象-虚拟网）与拓扑排序，以及AOE网（活动-对象-事件网）与关键路径分析。这些内容在项目管理和工程规划中具有实际应用价值，例如在项目进度管理中找出关键路径，确保任务按期完成。 最后，章节提及了图论的起源，欧拉的名字与哥尼斯堡七桥问题紧密相连，这个问题不仅启发了图论的发展，而且是欧拉回路概念的起源。欧拉回路是指在一个图中，可以从某个顶点出发，经过每条边恰好一次，然后返回起点的路径。欧拉回路的判定规则为判断是否存在这种路径提供了准则。 第6章“图”在《数据结构（C++版）》中深入剖析了图的理论和应用，是理解计算机科学中复杂数据结构和算法的关键环节，对于从事软件开发、数据分析等领域的人来说，掌握这部分内容至关重要。