2012年顶级期刊推荐系统算法综述：挖掘网络信息过滤的关键技术

4星 · 超过85%的资源需积分: 10 145 浏览量更新于2024-07-26 1 收藏 3.89MB PDF 举报

2012年的《Physics Reports》发表了一篇题为“Recommendersystems”的文章，该文献是对2012年国际顶级期刊中推荐系统算法和技术进行的深度综述。随着互联网的迅速扩张，用户面临的信息量急剧增长，推荐系统在信息过滤中的作用变得至关重要。文章作者包括来自阿里巴巴商学院、弗里堡大学、中国电子科技大学、阿斯顿大学和北京计算科学研究中心的研究者，他们在文章中探讨了推荐技术的发展和应用。文章的核心关注点在于以下几个方面： 1. **推荐系统的重要性**：文章强调了推荐系统在海量信息时代对于提高用户体验、提升用户满意度以及帮助用户发现个性化内容的关键作用。推荐技术通过分析用户行为数据，预测用户的兴趣偏好，从而为用户提供定制化的信息和服务。 2. **信息过滤与个性化推荐**：推荐系统被归类为信息过滤的一种形式，它利用算法（如协同过滤、基于内容的推荐、混合推荐等）对用户的历史行为、兴趣特征等进行分析，从而过滤出最相关的信息，减少用户搜索和筛选的时间。 3. **网络理论的应用**：论文提到了推荐系统如何结合网络理论，如社交网络、协同过滤网络，来挖掘用户之间的相似性和关联性，这有助于改进推荐的准确性。通过理解用户群体的行为模式，推荐系统能够更好地预测用户的未来行为。 4. **研究进展与算法发展**：2012年的研究可能涵盖了当时最新的推荐算法，例如深度学习、矩阵分解、排序学习等方法，这些技术通过处理复杂数据结构，提高了推荐的精确度和效率。 5. **文章历史和编辑信息**：这篇论文于2012年2月7日接受，并于同年3月6日在线发布。编辑为I. Procaccia，关键词包括推荐系统、信息过滤和网络，表明了研究的焦点集中在这些核心概念上。这篇文献提供了2012年推荐系统研究领域的关键洞察，为理解和设计更有效的推荐策略提供了宝贵的学术参考。随着科技的进步，后续的研究可能会进一步深化对用户行为理解、优化算法性能以及探索新兴技术在推荐系统中的应用。

L. Lü et al. / Physics Reports 519 (2012) 1–49 9

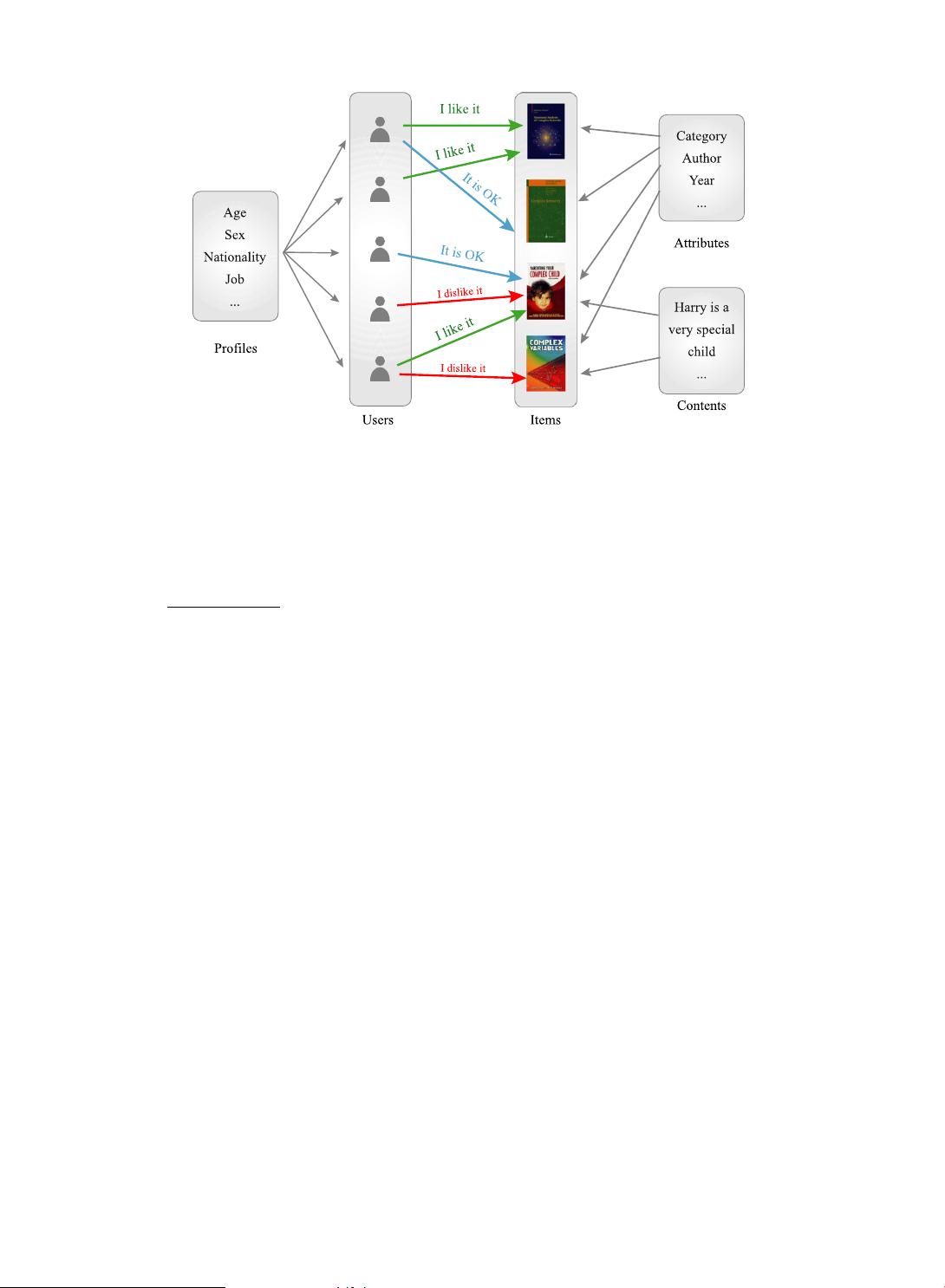
Fig. 4. Illustration of a recommender system consisted of five users and four books. The basic information contained by every recommender system is

the relations between users and objects that can be represented by a bipartite graph. This illustration also exhibits some additional information frequently

exploited in the design of recommendation algorithms, including user profiles, object attributes and object content.

max

(u) = 2k(u), while the minimal coordination number is z

min

(u) = 2n for n(n − 1) < k(u) ≤ n

and z

min

(u) = 2n + 1

for n

< k(u) ≤ n(n + 1), with n some integer. Obviously, a local tree structure leads to maximal coordination number,

while the maximum overlap corresponds to the minimal coordination number. Therefore, they define the hyperedge density

as [86]:

(u) =

max

(u) − z(u)

max

(u) − z

min

(u)

, 0 ≤ D

(u) ≤ 1. (7)

The definition of hyperedge density for resources and tags is similar. Empirical analysis indicates a high clustering behavior

under both metrics [82,86]. The study of hypergraph for the collaborative tagging networks has just been unfolding, and how

to properly quantify the clustering behavior, the correlations and similarities between nodes, and the community structure

is still an open problem.

(iv) average distance: defined as the average shortest path length between two random nodes in the whole network.

3.3. Recommender systems

A recommender system uses the input data to predict potential further likes and interests of its users. Users’ past

evaluations are typically an important part of the input data. Let M be the number of users and let N be the number of

all objects that can be evaluated and recommended. Note that object is simply as a generic term which can represent books,

movies, or any other kind of consumed content. To stay in line with standard terminology, we sometimes use item which has

the same meaning. To make the notation more clear, we restrict to Latin indices i and j when enumerating the users and to

Greek indices α and β when enumerating the objects. Evaluation/rating of object α by user i is denoted as r

iα

. This evaluation

is often numerical in an integer rating scale (think of Amazon’s five stars)—in this case we speak of explicit ratings. Note that

the common case of binary ratings (like/dislike or good/bad) also belongs to this category. When objects are only collected

(as in bookmark sharing systems) or simply consumed (as in online newspaper or magazine without rating systems) or

when ‘‘like’’ is the only possible expression (as on Facebook), we are left with unary ratings. In this case, r

iα

= 1 represents

a collected/consumed/liked object and r

iα

= 0 represents a non-existing evaluation (see Fig. 4). Inferring users’ confidence

levels of ratings is not a trivial task, especially from the binary or unary ratings. Accessorial information about users’ behavior

may be helpful, for example, the users’ confidence levels can be estimated by their watching time of television shows and

with the help of this information, the quality of recommendation can be improved [95]. Even if we have explicit ratings, it

does not mean we know how and why people vote with these ratings—do they have standards of numerical ratings or they

just use ratings to present orders? Recent evidence [96] to some extent supports the latter ansatz.

The goal of a recommender system is to deliver lists of personalized ‘‘recommended’’ objects to its users. To this end,

evaluations can be predicted or, alternatively, recommendation scores can be assigned to objects yet unknown to a given

user. Objects with the highest predicted ratings or the highest recommendation scores then constitute the recommendation

list that is presented to the target user. There is an extensive set of performance metrics that can be used to evaluate the

resulting recommendation lists (see Section 3.4). The usual classifications of recommender systems is as follows [15]:

1. Content-based recommendations: Recommended objects are those with content similar to the content of previously

preferred objects of a target user. We present them in Section 4.2.3.

10 L. Lü et al. / Physics Reports 519 (2012) 1–49

Table 2

Recommendation process in a nutshell: to estimate the potential favorable opinion

of Carol about Casablanca, one can use the similarity of her with those of Alice.

Alternatively, one can note that ratings of Titanic and Casablanca follow a similar

pattern, suggesting that people who liked the former might also like the latter.

Alice Bob Carol

Titanic 5 1 5

2001: A Space Odyssey 1 5 2

Casablanca 4 2 ?

2. Collaborative recommendations: Recommended objects are selected on the basis of past evaluations of a large group of

users. An example is given in Table 2. They can be divided into:

(a) Memory-based collaborative filtering: Recommended objects are those that were preferred by users who share similar

preferences as the target user, or, those that are similar to the other objects preferred by the target user. We present

them in Sections 4 (Standard similarity-based methods) and 7 (methods employing social filtering).

(b) Model-based collaborative filtering: Recommended objects are selected on models that are trained to identify patterns

in the input data. We present them in Sections 5 (dimensionality reduction methods) and 6 (diffusion-based

methods).

3. Hybrid approaches: These methods combine collaborative with content-based methods or with different variants of other

collaborative methods. We present them in Section 8.4.

3.4. Evaluation metrics for recommendation

Given a target user i, a recommender system will sort all i’s uncollected objects and recommend the top-ranked objects.

To evaluate recommendation algorithms, the data is usually divided into two parts: The training set E

and the probe set

. The training set is treated as known information, while no information from the probe set is allowed to be used for

recommendation. In this section we briefly review basic metrics that are used to measure the quality of recommendations.

How to choose a particular metric (or metrics) to evaluate recommendation performance depends on the goals that the

system is supposed to fulfill. Of course, the ultimate evaluation of any recommender system is given by the judgment of its

users.

3.4.1. Accuracy metrics

Rating accuracy metrics. The main purpose of recommender systems is to predict users’ future likes and interests. A

multitude of metrics exist to measure various aspects of recommendation performance. Two notable metrics, Mean Absolute

Error (MAE) and Root Mean Squared Error (RMSE), are used to measure the closeness of predicted ratings to the true ratings.

If r

iα

is the true rating on object α by user i,

iα

is the predicted rating and E

is the set of hidden user–object ratings, MAE

and RMSE are defined as

MAE =



(i,α)∈E

iα

−

iα

|, (8)

RMSE =





(i,α)∈E

iα

−

iα

)



1/2

. (9)

Lower MAE and RMSE correspond to higher prediction accuracy. Since RMSE squares the error before summing it, it tends

to penalize large errors more heavily. As these metrics treat all ratings equally no matter what their positions are in the

recommendation list, they are not optimal for some common tasks such as finding a small number of objects that are likely

to be appreciated by a given user (Finding Good Objects). Yet, due to their simplicity, RMSE and MAE are widely used in the

evaluation of recommender systems.

Rating and ranking correlations. Another way to evaluate the prediction accuracy is to calculate the correlation between

the predicted and the true ratings. There are three well-known correlation measures, namely the Pearson product-moment

correlation [97], the Spearman [98] correlation and Kendall’s Tau [99]. The Pearson correlation measures the extent to which

a linear relationship is present between the two sets of ratings. It is defined as

PCC =



(

−

r)(r

−





(

−





−

, (10)

where r

and

are the true and predicted ratings, respectively. The Spearman correlation coefficient ρ is defined in the

same manner as the Pearson correlation, except that r

and

are replaced by the ranks of the respective objects. Similarly

剩余48页未读，继续阅读

plljkkk

粉丝: 0
资源: 1

2012年顶级期刊推荐系统算法综述：挖掘网络信息过滤的关键技术

推荐系统调研报告及综述（张永锋）

个性化推荐系统的文献综述.docx

毕业论文-web系统文献综述(网上书店系统)

计算机专业文献综述怎么写

WG215wifi模块文献综述

宿舍管理系统的文献综述

含文献综述、外文翻译

如何使用你给我写文献综述

帮我写一篇相关的文献综述可以吗

请生成一篇认知风格的文献综述

最新资源