C++实现的红黑树详解及应用

"这篇资源主要介绍了红黑树的实现，以C++语言为载体，讨论了红黑树作为自平衡二叉查找树的特性和应用。文中提到了红黑树与二叉排序树、平衡二叉树（如AVL树）的关系，并详细阐述了红黑树的5大性质，以及在插入和删除操作后如何维护这些性质。同时，介绍了节点的旋转操作，如左旋和右旋，用于调整树的结构。" 红黑树是一种在计算机科学中广泛使用的自平衡二叉查找树，其设计理念是保持树的平衡，从而保证在插入、删除和查找操作时能保持较高的效率，通常为O(logn)的时间复杂度。相比于普通的二叉排序树，红黑树在最坏情况下也能保持较好的性能。 二叉排序树是一种特殊的二叉树，其中每个节点的值都大于其左子树中的所有节点值，小于其右子树中的所有节点值。然而，二叉排序树在极端情况下可能会退化成链表，导致性能下降。为了解决这个问题，引入了平衡二叉树，如AVL树，它要求左右子树的高度差不超过1，确保了查找效率。 红黑树则是更灵活的一种平衡策略，它允许节点有一定的不平衡，但是通过引入颜色属性（红色或黑色）以及特定的规则来保证树的整体平衡。红黑树的5大性质如下： 1. 每个节点要么是红色，要么是黑色。 2. 根节点是黑色。 3. 所有叶子节点（NIL节点，代表空节点）是黑色。 4. 如果一个节点是红色，则其两个子节点必须是黑色。 5. 对于每个节点，从该节点到其所有后代叶子节点的简单路径上，均包含相同数量的黑色节点。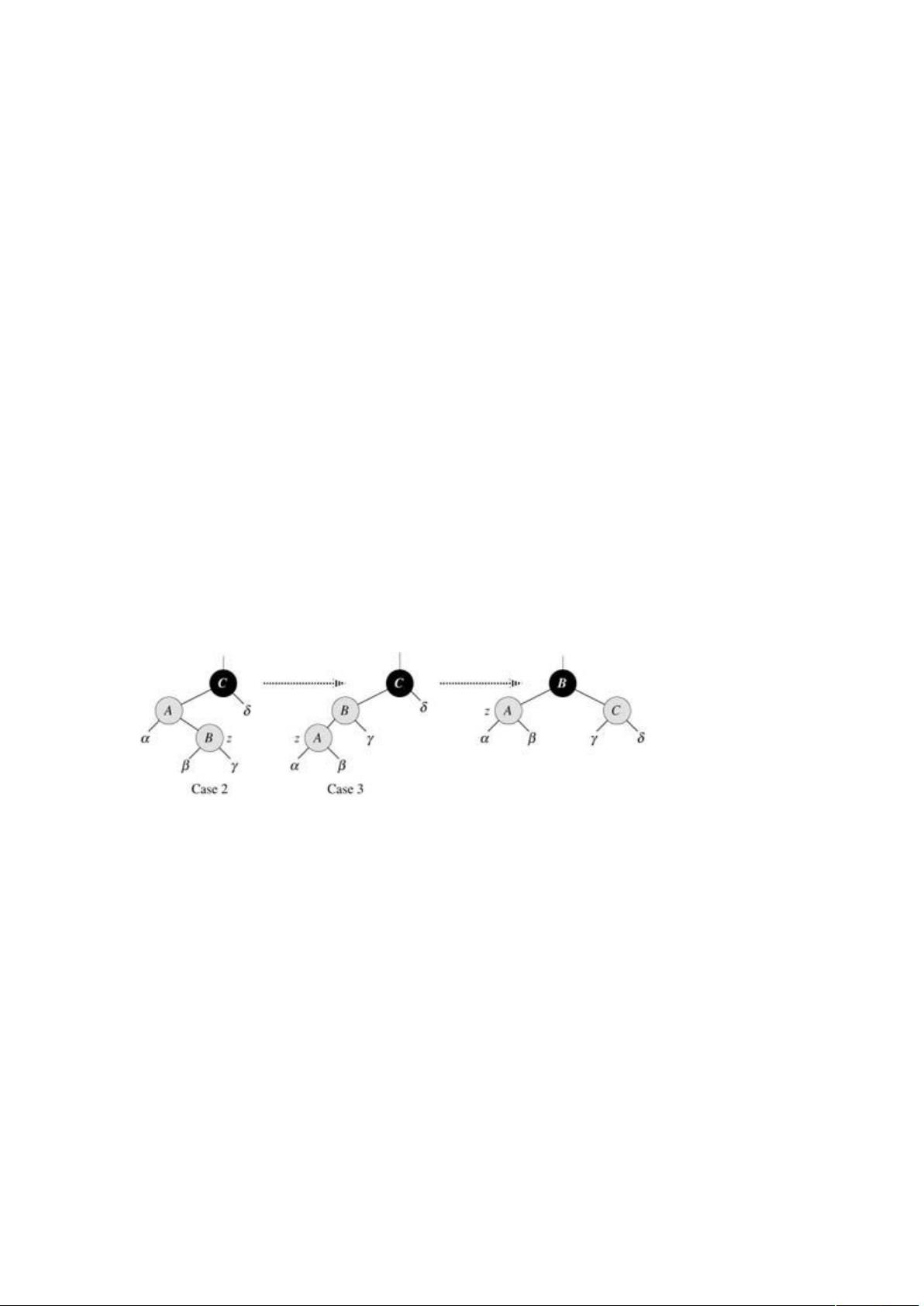 在插入新节点时，初始会将其标记为红色，这通常不会违反红黑树的性质。但如果插入操作导致了性质的破坏，就需要进行旋转和颜色调整。常见的调整操作包括左旋、右旋，以及可能的色变规则，如红红变黑、黑色兄弟变红等，以恢复树的平衡。 删除节点的情况更为复杂，可能需要重新着色和旋转多个节点来维持红黑树的性质。例如，删除一个黑色节点可能导致某些路径上的黑色节点数量减少，需要通过旋转和重新着色来恢复平衡。 红黑树在C++STL等许多库中都有广泛应用，比如在关联容器如`set`、`map`中，因为它能够提供高效的数据存取。理解并掌握红黑树的原理和操作对于优化数据结构和算法设计非常重要。