SAR ADC中分离电容DAC的线性校准技术

需积分: 41 17 浏览量更新于2024-09-07 2 收藏 297KB PDF 举报

"该文档详细探讨了在SAR(顺序比较型模数转换器)模数转换器中，分离电容DAC（CDAC）非线性问题及其解决方案。非线性主要源于桥式电容的失配和寄生效应。为了解决这一问题，文章提出采用可调谐电容器阵列进行校准，以改善线性度，并通过计算最小步长来控制调谐误差在0.5LSB以内。这种改进的调谐结构在保持电路复杂性不变的情况下，能实现更小的面积和更低的功耗。5b-5b分离DAC的行为仿真结果显示，相较于补偿电容阵列的原型，提出的校准方法能将信噪比(SNR)和失真比(SFDR)分别提升2.2dB和1.6dB。" 在SAR ADC中，CDAC是一个关键组件，它决定了转换器的精度和线性性能。传统的CDAC由一系列并联的电容组成，这些电容的开关选择组合形成不同的电容值，进而转换成数字信号。然而，由于制造工艺的不完美，桥式电容可能会出现失配，导致电容值的不精确，从而引入非线性误差。此外，寄生效应如电容的串联电阻、寄生电感等也会对线性度产生影响。文章首先深入分析了分离电容结构的非线性来源，揭示了失配和寄生效应如何影响CDAC的性能。接着，作者提出了线性调谐方法，这种方法通过微调电容值来减小非线性误差，从而提高转换器的线性度。线性调谐的关键在于找到合适的调谐步长，使得调谐误差能够控制在可接受的范围内，此处是0.5LSB。为了优化这个过程，文章提出了一个改进的可调谐结构。这个新结构不仅能够在校准期间保持良好的线性性能，而且还能减少面积和降低功耗。这是一项重要的优化，因为在许多应用中，尤其是便携式设备中，低功耗和小体积是至关重要的设计目标。通过5位5位分离DAC的仿真结果，文章展示了改进的校准方法的有效性。相比于传统的补偿电容阵列，新方法能够显著提升SNR和SFDR，这意味着在相同电路复杂性的前提下，转换器的动态性能得到了显著提升。SNR的提升意味着更高的信号质量，而SFDR的提升则意味着更强的抗干扰能力。该文档为SAR ADC中CDAC的非线性问题提供了一个有效的解决方案，即利用线性调谐的可调谐电容器阵列进行校准。这种方法不仅提升了转换器的线性度，还降低了功耗和物理尺寸，对于高性能模拟/电源设计领域具有重要的实践意义。

Calibration for Split Capacitor DAC in SAR ADC

Zhe Li

, Yuxiao Lu

, Tingting Mo

Center for Analog/RF IC (CARFIC), School of Microelectronics,

Shanghai Jiaotong University, Shanghai 200240, China

* Email: motingting@ic.sjtu.edu.cn

Abstract

The nonlinearity of split capacitor DAC (CDAC) in SAR

ADC is mainly caused by the mismatch and parasitic

effect of the bridge capacitor. A tunable capacitor array

for compensation can be a solution. This paper first

analyzes the nonlinearity of the split capacitor structure,

and then proves that the linear tuning method results in

linearity improvements and finally, an improved tunable

structure is proposed by calculating the minimal step

which keeps the tuning error within 0.5LSB. The new

implementation achieves smaller area and less power

consumption during the calibration, while maintaining

the same circuit complexity. Behavioral Simulations

based on a 5b-5b split DAC show that the proposed

calibration further improves SNDR and SFDR by 2.2dB

and 1.6dB, respectively compared with the prototype of

compensation capacitor array.

1. Introduction

Recent years have witnessed the rapid development

of charge-redistribution successive approximation

of its low power consumption, minimal analog featureˈ

and the intrinsic advantage from process scaling. In

high-resolution high-speed applications, however, the

SAR architecture is rarely seen due to various technical

barriers. One is large input capacitors, which causes

insufficient time settling and large power consumption.

For traditional binary-weighted capacitive DAC, the

input load capacitance and area increase exponentially

with the number of bits.

Driven by such demands, split capacitor structure is

introduced [1-4]. It can significantly attenuate the total

capacitance with a bridge capacitor added. However, the

fractional-value bridge capacitor is hard to match and is

highly sensitive to parasitic effect, and the linearity

would be thereby severely damaged. To calibrate the

above nonlinear elements, a charge domain

compensation focusing on the calibration of the top-plate

parasitic capacitor was proposed in [1]. Unfortunately,

the mismatch of fractional value capacitor itself was

ignored. [2] suggested an extra top-plate tunable

capacitor to ground. The tunable array improves the

linearity, but the structure remains to be optimized for

better calibration performance.

This paper proposes a modified structure promising

better calibration compared with [2]. The sequence of

this paper is to analyze the linearity performance of split

capacitor DAC at first, and then to prove the linear

tuning [2] of the compensation array results in a linear

SNDR improvement. By revealing how the different

tunable array affect the calibration performance, an

improved version is presented. The new tunable array is

area-efficient and power-saving during the calibration.

Behavioral simulations show that SNDR and SFDR are

improved 2.2dB and 1.6dB, compared with the method

in [2]. DNL and INL are optimized to +0.15/-0.15LSB

and +0.15/-0.18LSB, respectively.

2. Split DAC linearity analysis

The nonlinearity of SAR ADC is mainly caused by

non-binary weights due to capacitor mismatch and

parasitics. To examine the static random mismatch of

capacitors only, Monte Carlo simulation of a 10-bit

traditional binary-weighted DAC in 65nm process is

carried out. To achieve 0.5LSB INL for 10bit resolution

with 99% probability, the minimal capacitance is 20fF

for metal-oxide-metal (MoM) capacitors. In this case,

the total capacitance will count to 20.48pF, which is an

unacceptable size in terms of DAC settling, power

dissipation and physical area.

Split Capacitor DAC can effectively reduce the total

capacitance since the bridge capacitor C

separates the

DAC into an i-bit LSB and a j-bit MSB binary-scaled

sub-DAC. The equivalent total output capacitance is

reduced by

i-1

times compared to the conventional

structure. The bridge capacitor is usually placed in the

middle of the DAC array to obtain an optimal tradeoff

between the total capacitance and the standard deviation

of INL [3].

 

3

3

3

1RGH$ 1RGH%





9''

*1'



/6%

06%

9,1B1

ELWBQ!

())

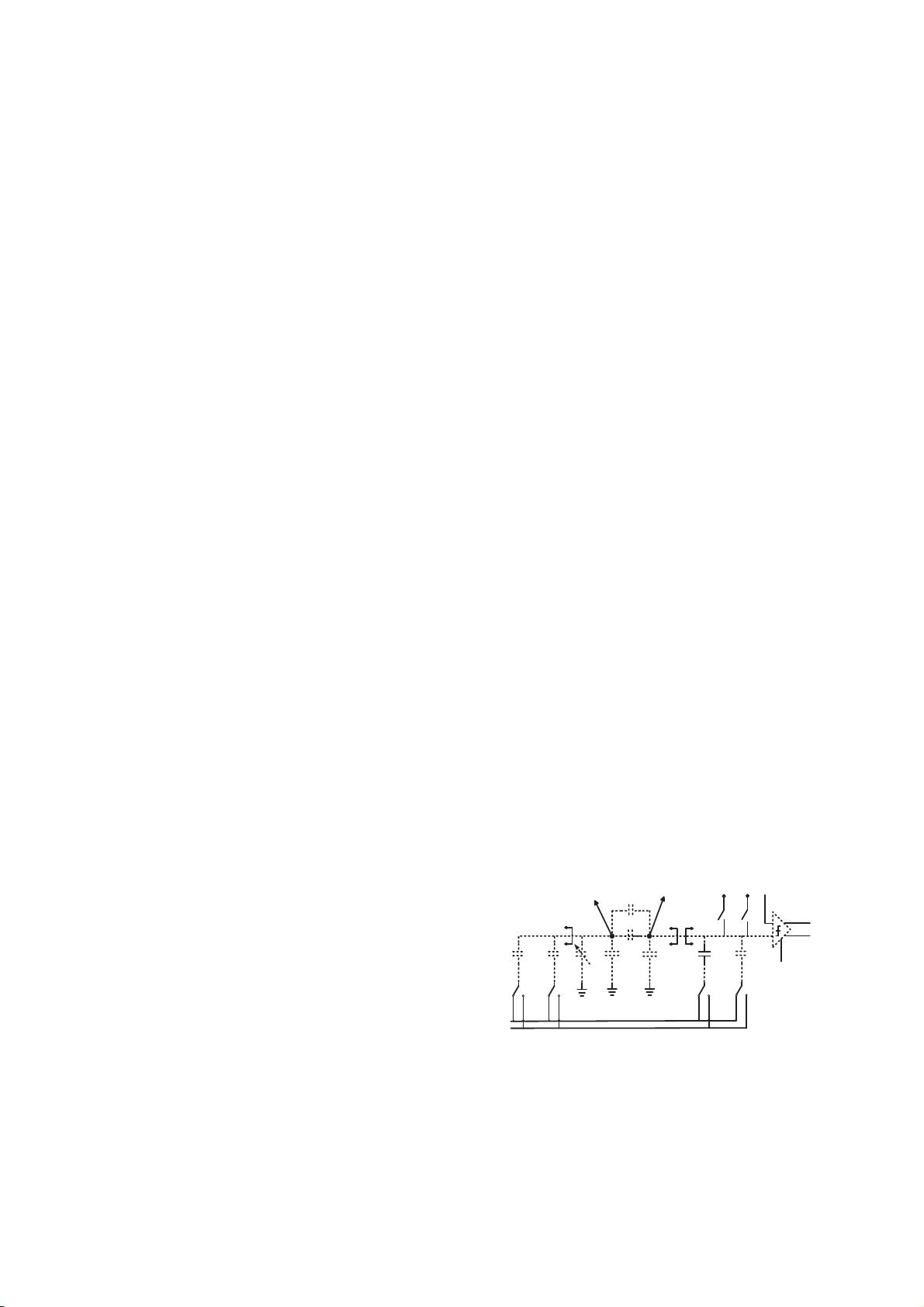
6$03

9&0

6:B9&0B1

&03B23

&03B21

ELWBQ! ELWBQ!

ELWBQ!

&03B&/.

7R'$&3SDUW

'$&1SDUW



Fig.1 Fully-differential 5b-5b split CDAC non-

ideal

model with tunable array C

下载后可阅读完整内容，剩余3页未读，立即下载

weixin_39841848

粉丝: 512
资源: 1万+

SAR ADC中分离电容DAC的线性校准技术

SAR 模数转换器中的分离电容DAC校准-综合文档

逐次逼近（SAR）模数转换器进展

带自校准的14位逐次逼近模数转换器设计

15_sar.pdf

ADC Architectures II-Successive Approximation ADCs.pdf

高速SAR ADC设计

一种18位SARADC的设计实现

一种非二进制数字校准方案：SAR ADC中分压DAC的应用

单片机ADC与DAC技术详解：模拟与数字世界的转换，感知物理世界的窗口

SAR ADC 的工作原理与优劣势分析

最新资源