小波分析基础：构造与时频工具应用详解

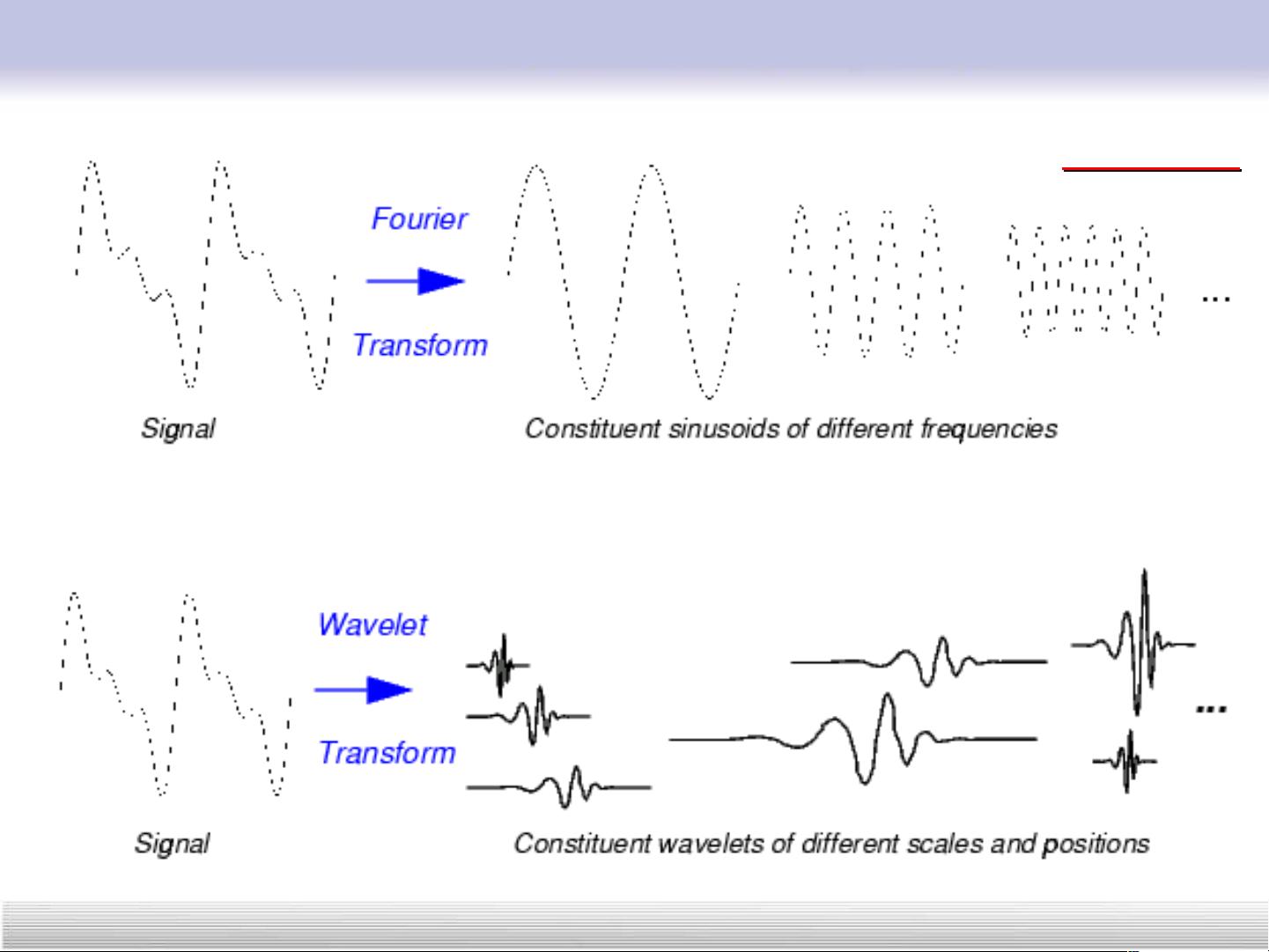
小波分析基础与小波变换是现代信号处理和数学分析中的重要工具，本PPT文档由河北大学数学与计算机科学学院提供，共68页，深入探讨了这一主题。首先，我们从数学的角度理解小波。小波被定义为在L2(R)空间（实数域上平方可积函数的空间）中构成正交基的基本元素，这些函数不仅有有限的能量，还满足特定的允许条件。这个概念的建立依赖于内积空间的概念，包括空间的分解和函数变换等基础知识。 从信号处理的角度看，小波变换是一种强大的时频分析工具。它是在解决傅立叶变换在处理非平稳信号时的局限性（如频率响应不随时间变化）的基础上发展起来的。因此，理解和掌握傅立叶变换、傅立叶级数以及滤波器等基础知识对于理解小波变换至关重要。傅立叶变换可以将信号从时域转换到频域，而小波变换则提供了更细致的时间-频率分析，它允许局部化的频率分析，这对于识别和处理复杂信号具有显著优势。 信号本身，无论是时间序列还是二维图像，都可以视为L2(R)或L2(R2)上的函数。例如，一张512x512像素的图像LENA，通过采样和量化将其转换为离散的数据，每个像素点的灰度值代表了图像在特定位置的亮度。图像分析时，小波变换能够捕捉到图像的局部特征，有助于降噪、边缘检测和图像压缩等应用场景。 小波变换的应用广泛，包括但不限于： 1. 图像处理：用于图像去噪、边缘检测、纹理分析等，如检测图像细节并保持高频信息。 2. 信号分析：在信号处理中，小波变换可以提供信号在不同时间尺度上的频率成分，有助于异常检测和故障诊断。 3. 数据压缩：由于小波变换的多分辨率特性，可用于高效的数据压缩算法，如JPEG 2000标准。 4. 信号分解：通过小波包分解，可以将复杂信号分解成多个不同频率和时间尺度的部分，便于分析和处理。 5. 自然语言处理：在文本挖掘和语音识别等领域，小波变换也有所应用，用于特征提取和模式识别。 小波分析基础和小波变换是一个涉及深厚的数学理论与实际应用相结合的领域，它的发展与进步极大地推动了信息技术的革新，特别是在信号处理和数据分析方面。通过学习和理解这一系列概念，可以大大提高我们在这些领域的研究和实践能力。