华南师大ACM线段树解决区间覆盖总长度问题

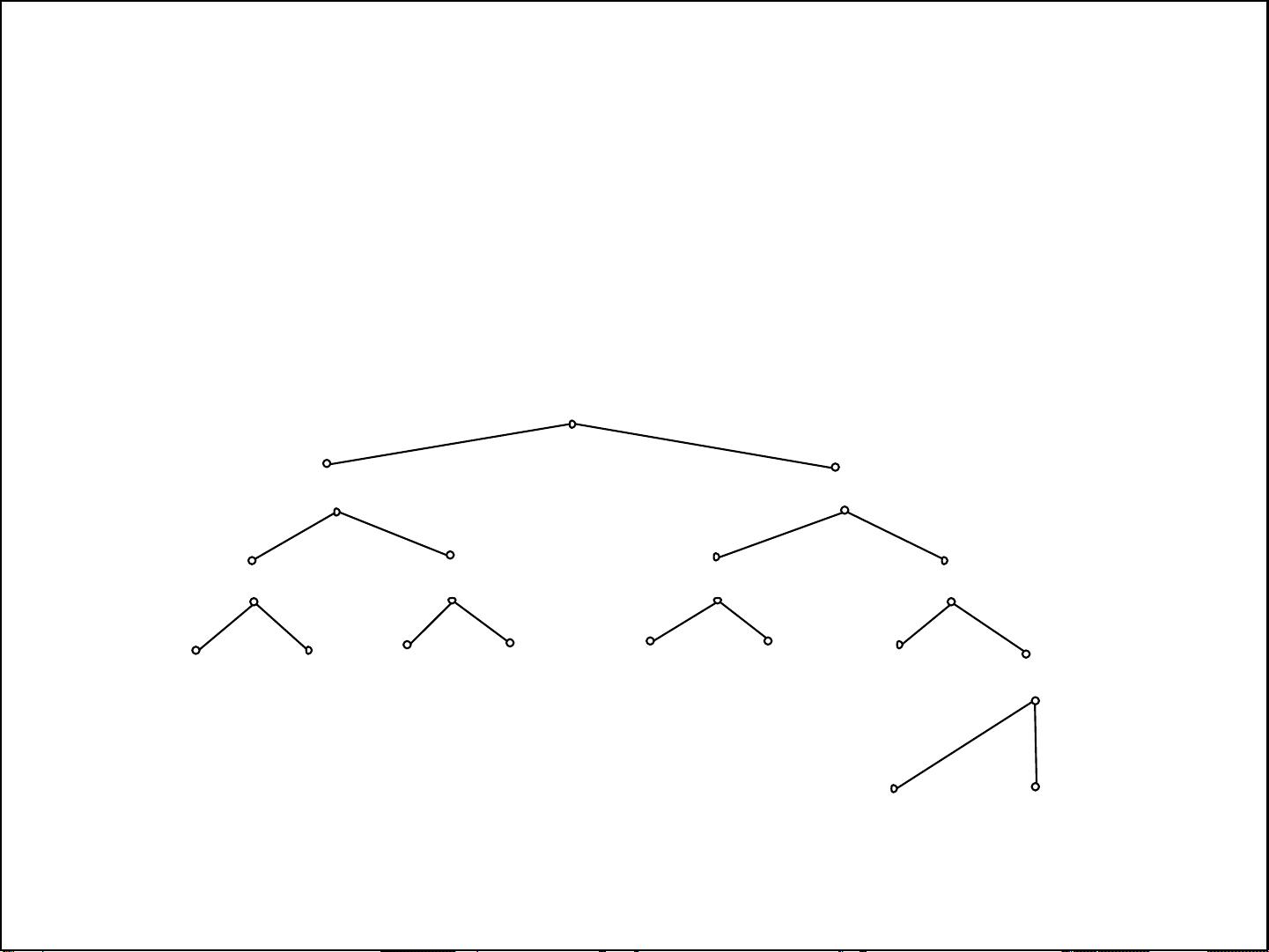
在ACM程序设计中，线段树是一种高效的数据结构，用于解决与区间查询相关的计算问题。例如，题目中提到的问题是一个经典的线段覆盖问题，即给定一系列线段，计算它们在X轴上覆盖的总长度。线段树能有效地处理这类问题，尤其是在线段数量较大且区间范围广泛时。 首先，理解问题的关键是将其抽象成计算机能够处理的形式。题目中的场景可以转化为线段的坐标对[min,max]，每个线段定义了一个区间，需要计算这些区间的并集长度。为了实现这一目标，我们有两种主要的离散化策略： 1. **点(单位为1的线段)为单位的离散化**: - 使用一维数组，数组长度为[min,max-1]，每个元素表示相应区间的长度，初始值为0。 - 对于每个线段，遍历区间内的所有点，将对应数组元素置为1。 - 最后，统计数组中1的个数即为覆盖长度。 - 这种方法的优点是简单直观，但时间复杂度为O(n^2)，当线段数量众多或区间范围很大时效率较低。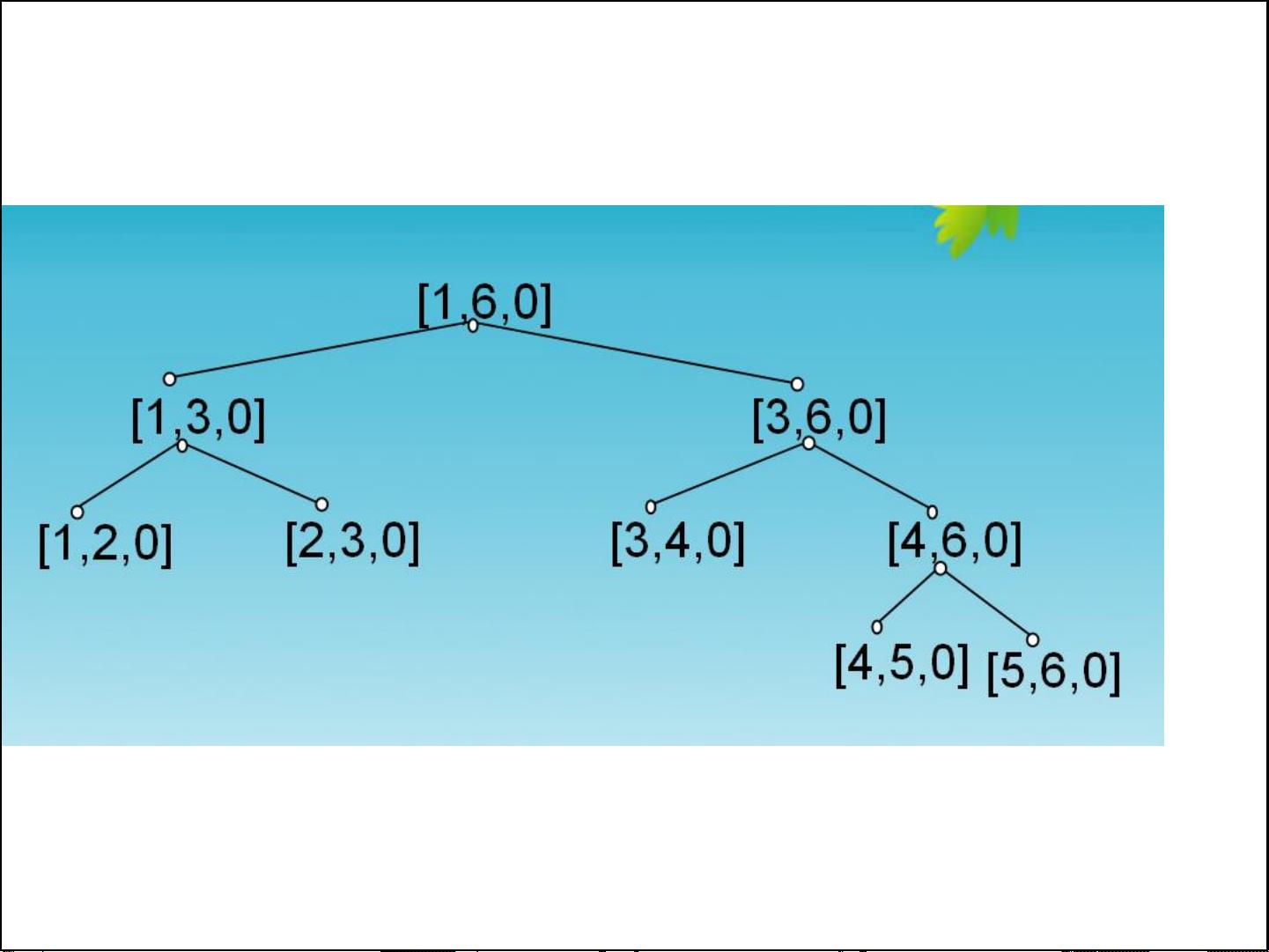 2. **以线段为单位的离散化**: - 先将所有线段的端点坐标排序，建立线段与其序号的映射关系。 - 将线段区间转换为序号，然后使用点为单位的方法计算。 - 结果通过线段序号反向转换回原坐标表示。 - 这种方法适用于线段数目较少的情况，因为它减少了实际的计算次数，从而提高了效率。 针对输入数据如[1,2][3,5][4,6][5,6]和更大的范围[10000,22000][30300,55000][44000,60000][55000,60000]，离散化二的线段离散化方法更为适用，因为它在处理大规模数据时具有更好的时间复杂度，避免了点枚举法中的平方级时间消耗。 在实际编程中，实现线段树通常涉及递归或者迭代的过程，利用树状结构存储区间信息，并进行区间合并操作。这不仅可以解决覆盖总长度的问题，还可以扩展到其他区间查询和修改的问题，比如计算线段树中某一区间内的元素个数、找到最大值或最小值等。线段树是ACM竞赛和实际编程中常见的高效数据结构，熟练掌握它的使用能提升解决问题的效率。