Python生成非均匀随机数：反变换法实现

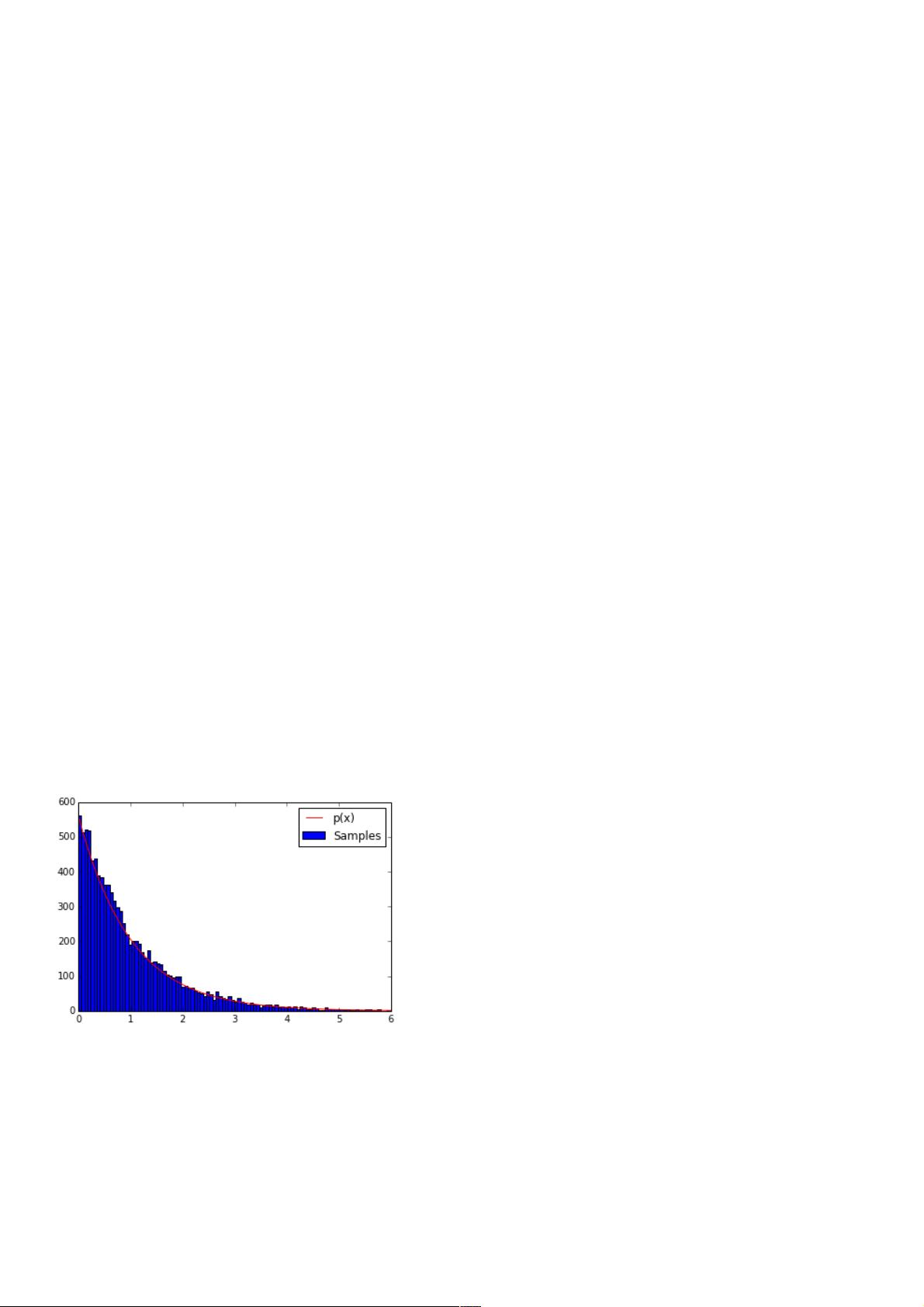
本文主要介绍了如何使用Python编程生成非均匀分布的随机数，特别是通过反变换法实现这一目标。反变换法是一种常见的方法，适用于已知分布函数的情况，通过求取分布函数的反函数来产生特定分布的随机数。 在统计学和模拟计算中，非均匀随机数的生成是十分重要的。当需要模拟符合特定概率分布的数据时，如正态分布、指数分布等，不能直接使用Python的`random`模块生成。反变换法提供了一种解决途径。该方法基于一个基本原理：若有一个在[0,1]区间内的均匀分布随机数R，可以通过找到分布函数F(x)的反函数F-1，将R转换为符合F(x)分布的随机数X，即X = F-1(R)。 首先，反函数的存在性是关键。对于单调递增的分布函数F(x)，它必然存在反函数。这是因为F(x)在定义域内是单射的，即每个x值对应一个唯一的F(x)值，因此可以找到一个函数F-1将F(x)映射回x。 以一个具体的例子来说明，假设我们希望在[0, 6]区间上生成随机数，其概率密度函数近似为P(x) = e^(-x)。这代表了一个指数分布。首先，我们需要计算这个分布的累积分布函数（CDF）F(x) = 1 - e^(-x)。接着，找到CDF的反函数invCDF = -ln(1-x)。确定了这些，就可以在[0,1]范围内生成随机数R，然后通过invCDF(R)计算出对应的非均匀分布随机数X。 在Python中，我们可以使用`numpy`和`matplotlib`库进行实现。首先定义概率密度函数p(x)和CDF F(x)，然后计算其反函数invCDF。设置随机数生成的范围，生成N个在rmin和rmax之间（对应CDF的值）的均匀随机数R，通过invCDF将这些值转换为X。最后，使用`numpy.histogram`计算直方图，并利用`matplotlib`绘制直方图与理论分布曲线进行对比，以验证生成的随机数是否符合预期的分布。 通过这种方式，我们可以灵活地生成符合各种非均匀分布的随机数，这对于模拟实验、统计分析和建模等应用非常有用。此外，还可以探索其他生成非均匀随机数的方法，例如接受-拒绝法或盒-Muller变换等，以适应不同情况的需求。