最优化理论基础：线性规划详解与凸集概念

"最优化之线性规划，包括图解法、单纯形法和Karmarkar算法。" 线性规划是一种重要的最优化方法，它主要用于寻找一组变量的线性组合，使得在满足一系列线性约束条件下，目标函数达到最大值或最小值。在实际应用中，线性规划广泛应用于生产计划、资源配置、投资决策等领域。 线性规划的基本元素包括决策变量、目标函数和约束条件。决策变量是待求解的未知数，它们的取值直接影响目标函数的优化结果。目标函数通常表示为决策变量的线性组合，是需要最大化或最小化的量。约束条件则限制了决策变量的可行域，通常表现为决策变量的线性不等式或等式。 1. 凸集与凸函数 - 凸集是线性规划的基础概念。如果集合S中的任意两点的线性组合仍在这个集合内，那么S就是凸集。例如，超平面和半空间都是凸集。 - 凸函数是定义在凸集上的函数，其性质是任意两点的线性组合的函数值不会超过这两点函数值的线性组合。凸函数在最优化中有着重要的地位，因为它保证了局部最优解也是全局最优解。 2. 单纯形法 - 单纯形法是求解线性规划问题的一种经典方法，由George Dantzig于1947年提出。这种方法通过在当前解的基础上，选择一个改进方向来逐步逼近最优解。每次迭代中，单纯形法会选择一个新的基变量进入基，同时移出一个基变量，直到找到满足所有约束且目标函数最优的解。 3. Karmarkar算法 - Karmarkar算法是由 Narendra Karmarkar 在1984年提出的，它是第一个实用的多项式时间复杂度的线性规划算法，显著提高了大规模线性规划问题的求解效率。该算法基于内点法，通过迭代改变决策变量的值，确保在每次迭代中都能缩小解的空间，直至找到最优解。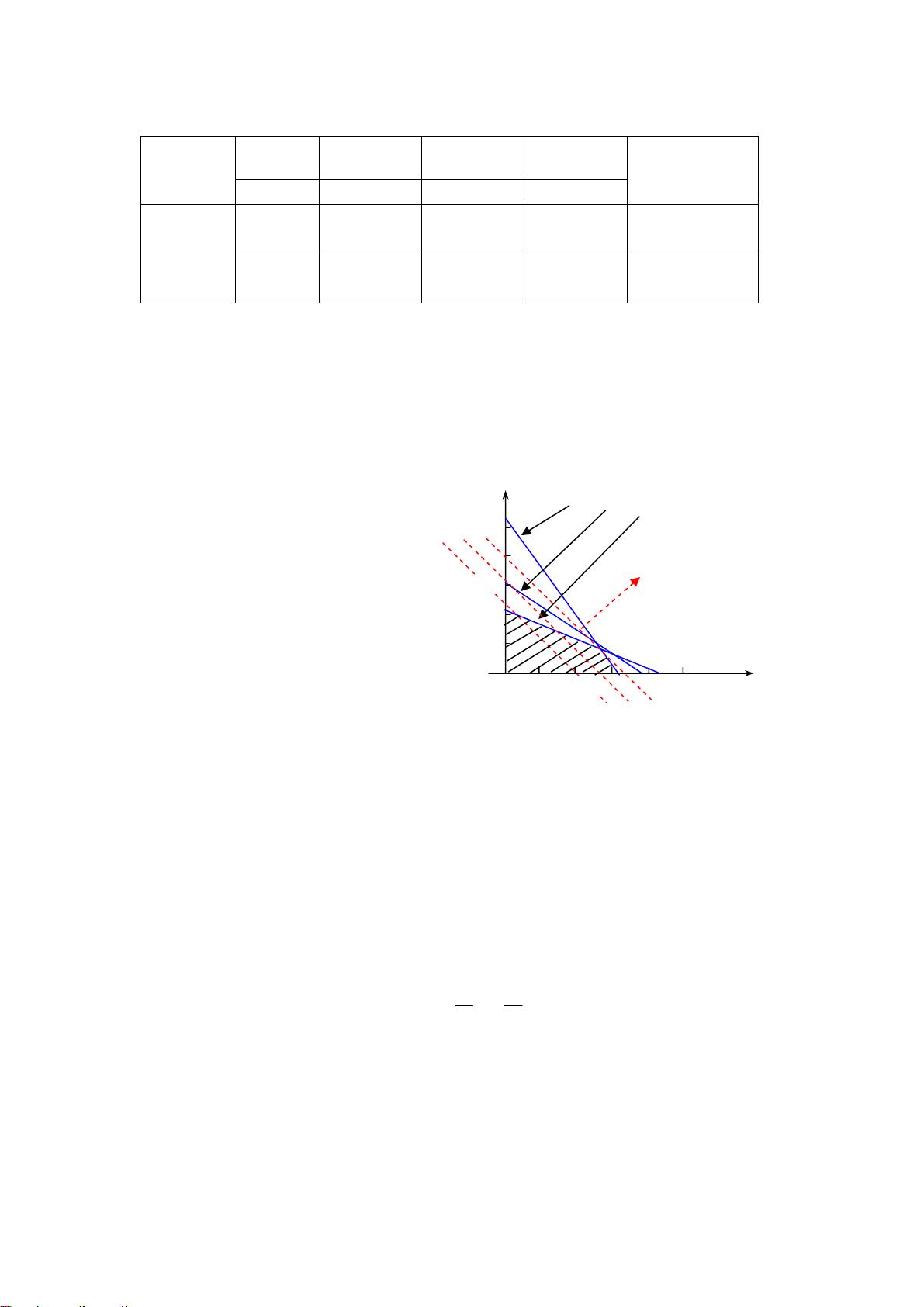 线性规划问题的解决方案通常分为图解法（如二维问题的图形解法）和数值方法（如单纯形法和Karmarkar算法）。对于复杂的线性规划问题，数值方法更具有优势，尤其是在处理大量约束和变量的情况下。 除了线性规划，最优化理论还包括整数规划（其中决策变量必须取整数值）、非线性规划（目标函数或约束是非线性的）、几何规划、动态规划、随机规划和网络决策等。这些理论和技术构成了现代最优化方法的基石，为解决实际问题提供了强有力的工具。