主成分分析PCA入门：降维与信息保留

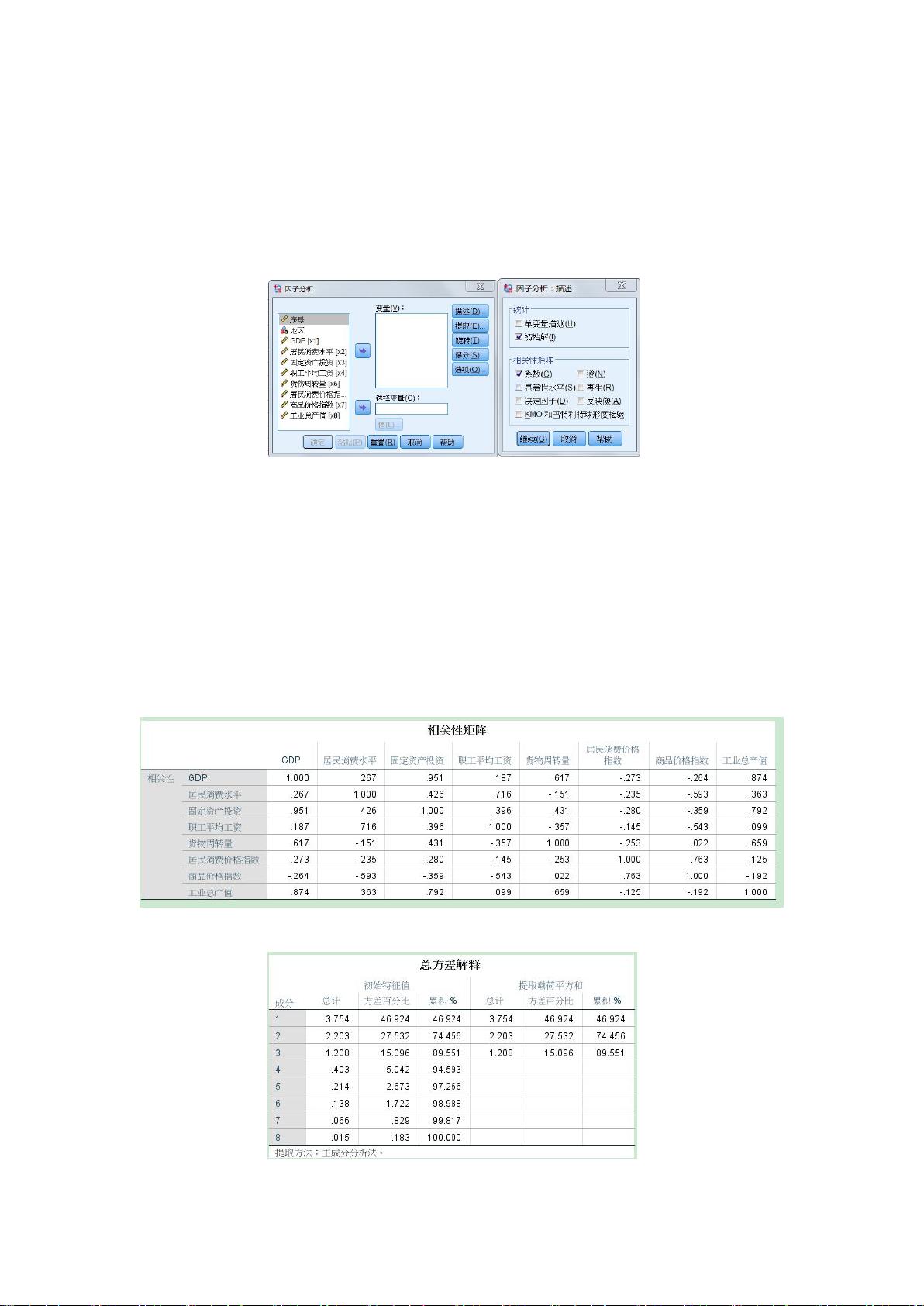
"主成分分析与因子分析1" 本文主要探讨了主成分分析（PCA）这一数据降维方法。PCA是一种广泛使用的统计技术，旨在通过转换原始变量为新的线性组合，即主成分，来降低数据的复杂度，同时最大化保留原始数据的信息。这种方法对于机器学习模型的训练和预测非常有用，因为它可以减少计算复杂性，提升效率。 主成分有以下几个关键特性： 1. 它们是原始变量的线性组合。 2. 主成分的数量通常小于原始变量的数量，这有助于降低维度。 3. 主成分保留了原始变量的大部分信息。 4. 主成分之间相互独立，这意味着它们不包含重复的信息。 PCA的几何意义可以从坐标变换的角度理解。它通过旋转将原始数据从初始坐标系转换到新的坐标系，新坐标系中的第一个主成分（F1轴）最大化了数据的方差，而后续的主成分则按方差大小依次排列。这样，我们可以通过少数几个主成分来概括大部分原始信息，从而实现降维。 在数学上，PCA基于样本的协方差矩阵或相关矩阵。假设我们有n个样本，每个样本有p个指标，形成一个n×p的原始数据矩阵X。PCA的目标是找到一组正交基，使得数据投影到这些基上后的方差最大。这可以通过对协方差矩阵进行特征分解来实现，得到特征值和对应的特征向量。特征值反映了每个主成分的重要性，而特征向量定义了主成分的方向。 在实际应用中，通常选择那些具有较大特征值的主成分，因为它们能解释更多的数据方差。Cattell的碎石检验是一种常用的判断标准，通过绘制特征值的图形来决定应保留哪些主成分。当特征根大于1时，通常认为对应的主成分具有足够的解释力，应当被保留。 PCA的其他线性降维方法还包括独立成分分析（ICA）、线性判别分析（LDA）和局部线性嵌入（LFA）。同时，非线性降维方法如核主成分分析（KPCA）、核 Fisher 分类（KFDA）、Isomap、局部线性嵌入（LLE）、拉普拉斯嵌入（LE）和局部保持投影（LPP）等也是常用的数据降维工具。 总结来说，主成分分析是一种强大的工具，用于处理高维数据并提取其中的主要信息。通过有效地降维，PCA可以帮助我们更好地理解和可视化数据，同时也优化了数据分析和机器学习任务的性能。