小波分析基础与应用概览

"小波讲义" 小波分析是一种数学工具，它结合了频率和时间分析的优点，使得信号处理在时间和频率上具有更好的局部化特性。小波理论源自多个领域，包括数学、物理学、工程学以及计算机科学。本讲义旨在深入浅出地介绍小波分析的基本概念、历史背景及其在信号处理中的应用。 1. 小波定义与特性 - 小波（wavelet）是一类具有有限支撑或快速衰减特性的振荡函数。它可以被视为信号处理中的“构建块”，类似于傅里叶级数中的复指数函数。小波函数通常用ψ(x)表示，其特征在于能够在时间和频率域内提供精细的分辨率。 - 小波具有时间-频率局域性，这意味着它们能够同时捕捉信号的时间变化和频率成分。与传统的傅里叶变换相比，小波变换可以在不牺牲频率信息的情况下，更好地定位信号的瞬时特性。 - 快速变换算法是小波分析的一个重要优势，它们允许高效地进行小波系数计算，这对于大规模数据处理和实时应用至关重要。 2. 小波的历史与发展 - 小波分析的起源可以追溯到1807年Joseph Fourier提出的傅里叶分析。傅里叶分析将任何周期函数表示为正弦和余弦函数的无穷级数，但无法提供时间上的细节信息。 - 在20世纪，随着量子力学的发展，海森堡不确定性原理强调了时间-频率局域性的重要性，这为小波理论的发展奠定了基础。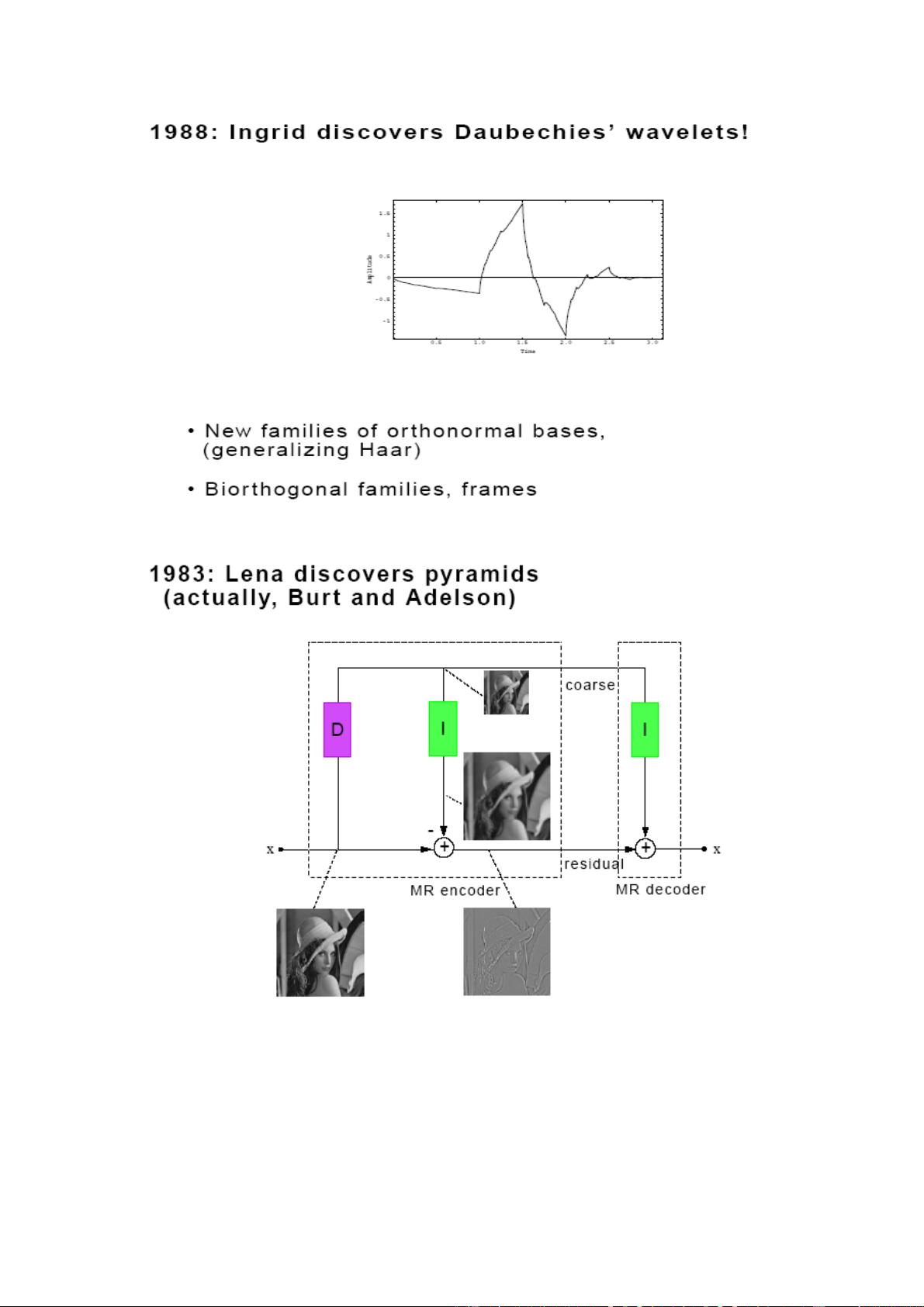 - 1980年代，法国数学家Maurice Allais和Jean Morlet引入了一种新的分析方法，后来被称为Morlet小波，这标志着现代小波分析的开端。随后，由Stanley Mallat发展的小波多分辨率分析进一步推动了该领域的进步。 3. 小波分析的数学基础 - 基于小波函数ψ(x)，可以构建小波级数来逼近任意函数f(x)。这个级数是小波系数cλ和相应小波函数ψλ(x)的线性组合。 - 小波变换通过改变尺度参数λ和位置参数a，可以得到不同尺度和位置的小波图像，这些图像揭示了信号在不同时间尺度上的结构和特征。 4. 小波的应用 - 在信号处理中，小波分析常用于噪声去除、压缩编码、故障诊断等任务，因为它可以有效地捕获信号的突变和局部特征。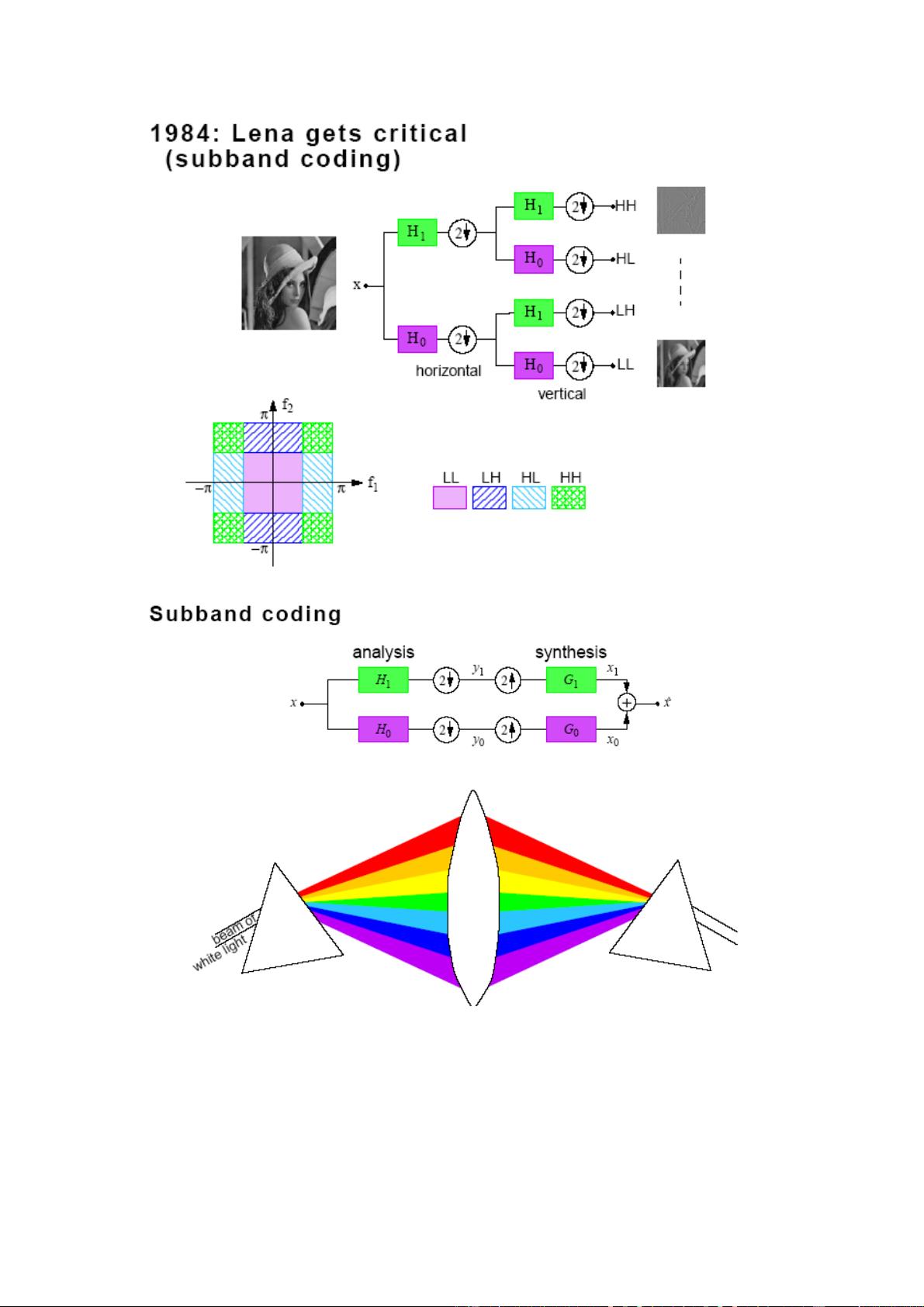 - 在图像处理领域，小波可用于图像压缩、边缘检测和图像复原。 - 在金融数据分析中，小波可以帮助识别市场的短期波动和长期趋势。 - 此外，小波还应用于地震学、医学成像、模式识别等诸多领域。 推荐的参考资料： 1. S.Mallat的《A Wavelet Tour of Signal Processing》提供了深入的小波理论和技术。 2. 崔锦泰的《小波分析导论》适合初学者了解小波的基础知识。 3. 程正兴的《小波分析算法与应用》详细介绍了小波在实际问题中的应用方法。 通过学习以上内容，你可以对小波分析有全面的理解，并能够利用小波理论解决实际问题。对于进一步研究，可以访问提供的参考网站获取更多资料。