MATLAB多元线性回归分析实战教程

"MATLAB中多元线性回归的例子PPT课件.ppt" 在MATLAB中，多元线性回归是一种用于分析多个自变量与一个因变量之间关系的统计方法。这个例子通过PPT课件的形式详细介绍了如何在MATLAB中执行多元线性回归分析。以下是关于这个主题的详细说明： 1. **线性回归函数**： MATLAB提供了`regress`函数来执行线性回归分析。基本语法是`b = regress(y, X)`，其中`y`是因变量的列向量，`X`是包含1（截距项）和所有自变量的矩阵。`b`将返回估计的回归系数。 2. **函数参数扩展**： `regress`函数还可以接受额外的参数`alpha`，用于指定显著性水平，默认为0.05。完整语法为`[b, bint, r, rint, s] = regress(y, X, alpha)`。`bint`返回回归系数的置信区间，`r`是残差向量，`rint`是残差的置信区间，而`s`则包含决定系数`R^2`、F统计量以及其对应的概率p值。 3. **统计分析**： - **决定系数** (`R^2`) 表示模型解释因变量变异的比例，其值介于0到1之间，越接近1表示模型拟合度越好。 - **F统计量** 用于检验整个模型的显著性，如果F值对应的概率`p`小于预先设定的显著性水平（如0.05），则认为回归模型整体上是显著的。 - **p值** 如果`p < α`，则拒绝零假设，即至少有一个自变量与因变量有关联，模型有效。 4. 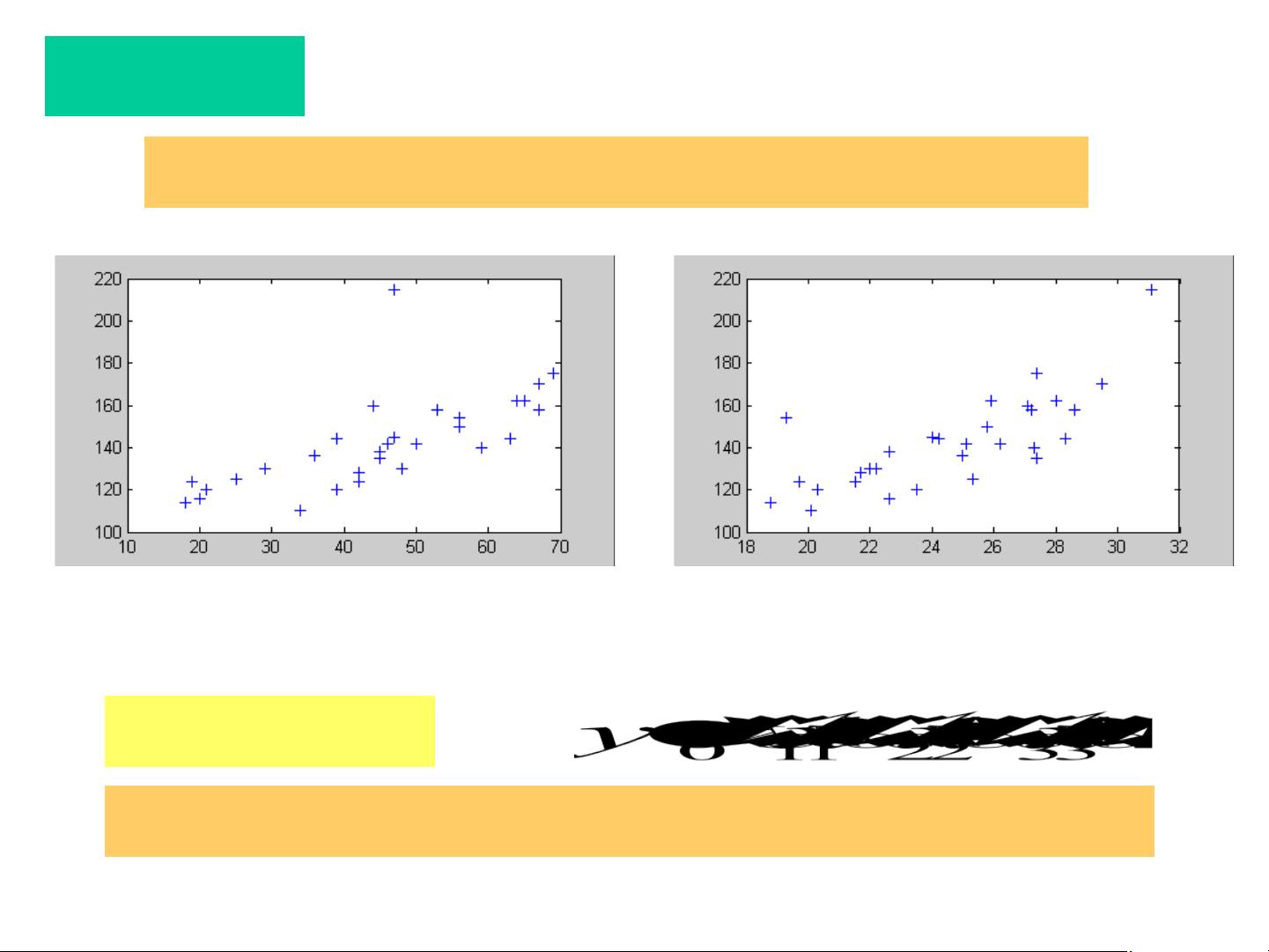**实例应用**： 以血压、年龄、体重指数和吸烟习惯为例，展示了如何构建多元线性回归模型。在这个例子中，血压是因变量，年龄、体重指数和吸烟习惯是自变量。通过计算各变量之间的相关性并画出散点图，可以初步观察它们之间的关系。 5. **模型建立**： 建立的线性回归模型形式为`y = α0 + α1*x1 + α2*x2 + α3*x3 + ε`，其中`α0, α1, α2, α3`是待估计的回归系数，`ε`是随机误差项。通过数据估计这些系数，构建回归方程。 6. **数据处理**： 示例中提供了30个观测点的数据，分别对应30个人的血压、年龄、体重指数和吸烟习惯。这些数据被用于计算回归系数和进行模型验证。 7. **图形分析**： 散点图可以用来可视化因变量与每个自变量之间的关系。例如，分别画出血压与年龄、体重指数的散点图，可以帮助理解它们之间的趋势。 8. **残差分析**： 使用`rcoplot(r, rint)`函数可以绘制残差及其置信区间图，这有助于评估模型的残差是否满足正态分布和独立性假设，以及检查是否存在异常值。 MATLAB中的多元线性回归提供了一种强大的工具，用于分析多个自变量如何影响一个因变量，并可以通过统计测试来评估模型的适用性和预测能力。在实际应用中，理解这些概念和操作步骤对于数据建模和分析至关重要。