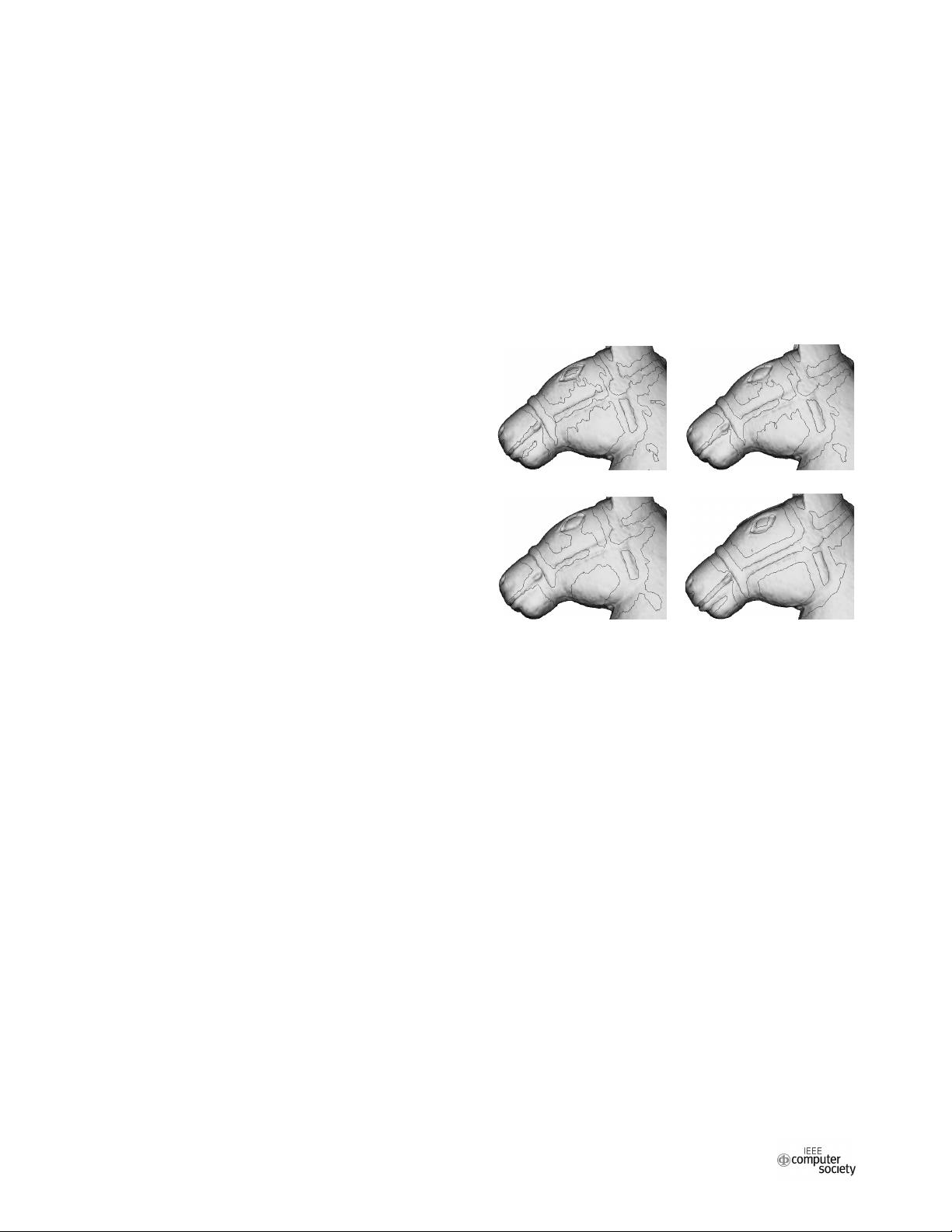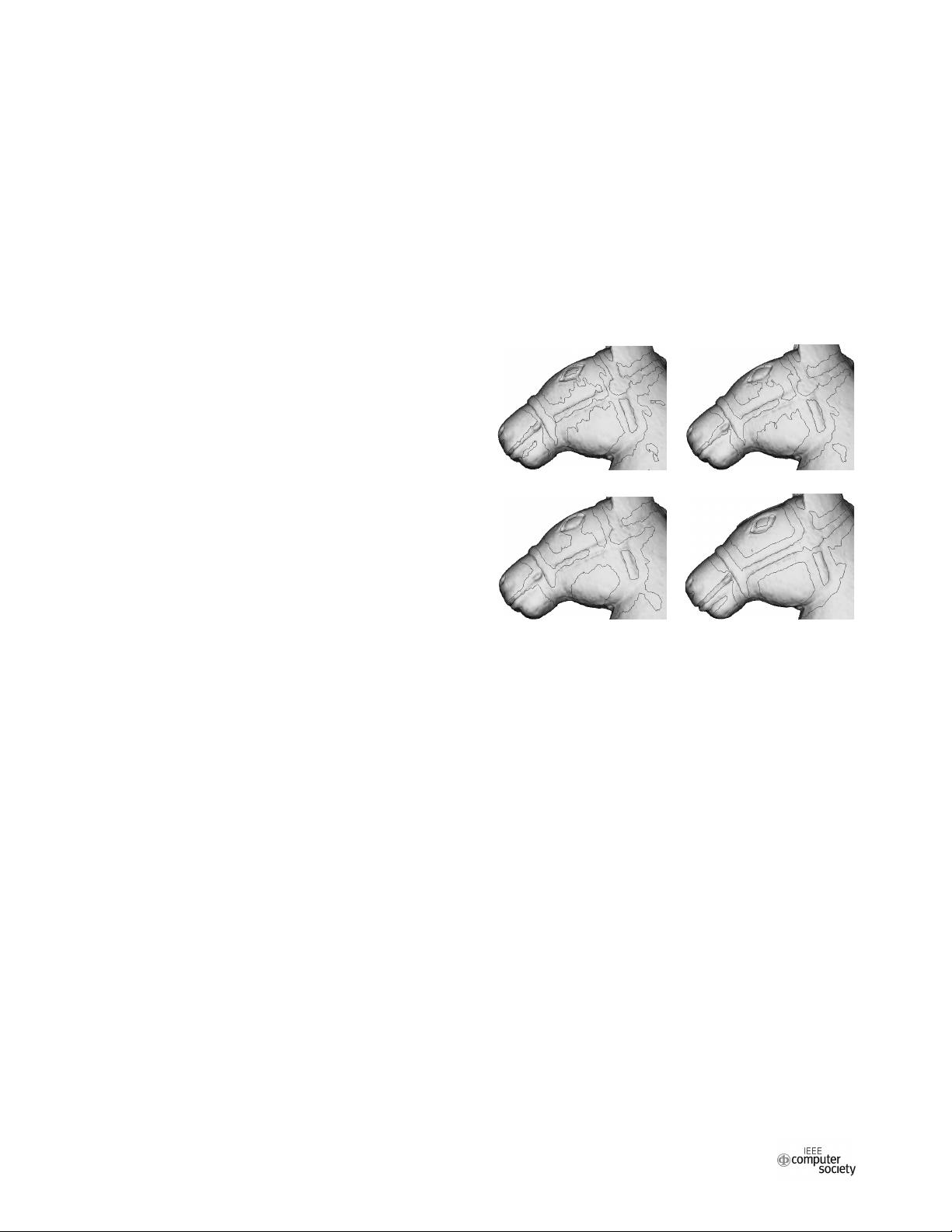
Multi-Scale Curve Detection on Surfaces
Michael Kolomenkin
Technion
michael.kolomenkin@gmail.com
Ilan Shimshoni
The University of Haifa
ishimshoni@is.haifa.ac.il
Ayellet Tal
Technion
ayellet@ee.technion.ac.il
Abstract
This paper extends to surfaces the multi-scale approach
of edge detection on images. The common practice for de-
tecting curves on surfaces requires the user to first select the
scale of the features, apply an appropriate smoothing, and
detect the edges on the smoothed surface. This approach
suffers from two drawbacks. First, it relies on a hidden
assumption that all the features on the surface are of the
same scale. Second, manual user intervention is required.
In this paper, we propose a general framework for auto-
matically detecting the optimal scale for each point on the
surface. We smooth the surface at each point according to
this optimal scale and run the curve detection algorithm on
the resulting surface. Our multi-scale algorithm solves the
two disadvantages of the single-scale approach mentioned
above. We demonstrate how to realize our approach on two
commonly-used special cases: ridges & valleys and relief
edges. In each case, the optimal scale is found in accor-
dance with the mathematical definition of the curve.
1. Introduction
3D feature curves on surfaces carry important informa-
tion regarding the shape of the object. Therefore, a lot
of effort has been devoted to charactering curves and de-
tecting them. Examples of types of curves include ridges
& valleys [19], parabolic curves [8], zero-mean curvature
curves [8], demarcating curves [9], and relief edges [10], to
name a few. Each type of curve is used to detect a different
3D feature. Curves on surfaces are equivalent to edges in
images, which are basic low-level features in images. Con-
sequently, 3D curves are inherently important in 3D shape
analysis.
In images, each edge is associated with a scale. This
scale is related to the image gradient; the steeper and
stronger the edge, the smaller the scale. This is because
steep edges are thinner, occupying a smaller area in the im-
age than fuzzy moderate edges. This concept exists also in
3D curves on surfaces. For instance, the eye of the horse in
Figure 1 has a smaller scale than its harness.
(a) Smallest-scale curves (b) Average-scale curves
(c) Large-scale curve (d) Our multi-scale curves
Figure 1. The benefit of using multi-scale curves. When relief
edges [10] are detected using a single scale, some features are
missed and others are inaccurate (a)-(c). Conversely, when using
multiple scales, the detected curves are more correct (d).
As illustrated in Figure 1, no single scale suffices to cap-
ture all the features. If the scale is too large, fine details
are missed. On the other hand, if the scale is too small,
coarse features are localized inaccurately and false features
appear. However, most state-of-the-art curve detection al-
gorithms use a single scale [1, 5, 9, 10, 19]. Moreover, the
user is required to manually choose the “correct” scale.
Our goal is to propose a general framework for automat-
ically estimating the optimal scale at each point on the sur-
face. This general scheme can then be applied to every type
of 3D curve, assuming it can be defined by the curvature and
its derivatives. Hence, our technique not only eliminates the
needed user intervention, but is also able to detect feaures
of different scales on a single object.
A couple of algorithms address scale selection. Pauly
et al. [20] propose a scheme that is designed for a single
type of curves, defined as the loci of points whose curvature
variation is persistent over all scales. It cannot be applied
in a straightforward manner to other types of curves. Luo et
al. [14] propose a method that is independent of the curve
2013 IEEE Conference on Computer Vision and Pattern Recognition
1063-6919/13 $26.00 © 2013 IEEE
DOI 10.1109/CVPR.2013.36
225
2013 IEEE Conference on Computer Vision and Pattern Recognition
1063-6919/13 $26.00 © 2013 IEEE
DOI 10.1109/CVPR.2013.36
225
2013 IEEE Conference on Computer Vision and Pattern Recognition
1063-6919/13 $26.00 © 2013 IEEE
DOI 10.1109/CVPR.2013.36
225