数字信号处理：插值与降采样教程

需积分: 10 192 浏览量更新于2024-07-19 1 收藏 2.6MB PDF 举报

"Interpolation and decimation of digital signals" 在数字信号处理领域，多速率信号处理的概念正在变得越来越重要，这涉及到使用不止一个采样率的信号处理算法。本文提供了一个关于应用于抽取（decimation）和插值（interpolation）系统的多速率数字信号处理的教程式综述。首先，基于采样定理建立了一个理论模型，然后展示了如何设计各种结构来有效地实现这些系统。此外，讨论了线性时不变组件（即数字滤波器）的设计技术，并提出了多级实现以提高效率的理念。 1. 采样与多速率信号处理采样是将连续信号转化为离散数据点的过程，根据奈奎斯特定理，为了无失真地恢复原始信号，采样频率必须至少是被采样信号最高频率的两倍。多速率信号处理涉及不同采样率之间的转换，这对于信号的压缩、扩展以及在不同速率系统间传递信号非常关键。 2. 插值与抽取插值是一种增加信号采样率的方法，通过在现有样本之间插入新的样本点，从而提高信号的分辨率。而抽取则是降低采样率的过程，通常通过丢弃某些采样点来实现。这两个过程都伴随着信号的滤波操作，以避免引入失真。 3. 数字滤波器设计在多速率处理中，数字滤波器是核心组件，用于去除或保留特定频率成分。设计滤波器时，通常考虑线性相位、稳定性、频率响应以及计算效率等因素。IIR（无限 impulse response）和FIR（有限 impulse response）滤波器是两种常见的数字滤波器类型，它们各有优缺点，可以根据具体应用选择。 4. 结构优化与多级实现为了提高系统效率，可以采用多级结构来实现插值和抽取。这种分阶段的方法可以分解复杂滤波器，减少计算量，同时保持良好的性能。例如，通过预滤波器和后滤波器的组合，可以简化主滤波器的设计，同时降低对硬件资源的需求。 5. 总结本文全面概述了多速率信号处理在数字信号插值和抽取中的应用，不仅提供了理论基础，还讨论了实际系统设计中的关键技术和策略。这些概念和技术广泛应用于通信、音频处理、图像处理等多个领域，对于提升系统的性能和效率具有重要意义。

CROCHIERE AND RABINER: INTERPOLATION AND DECIMATION

SIGNALS

305

and from (1 3) y

(m)

can be expressed in terms of

u(k)

y(m)

v(Mm).

(45)

Combining

(44)

and (45) gives

y(m)

h(Mm

rL)x(r)

(46)

r=-a0

and making the change of variables

and applying (3

gives

(47)

It is seen

that

(48) corresponds to the general form of the

time-varying digital-todigital conversion system described by

(6) and that the time-varying unit sample response

g,(n)

can

be expressed as

gm(n)

(nL

L),

for all

and all

(49)

where

h(k)

the time-invariant unit sample response of the

low-pass digital filter at the sampling rate

[

Similarly, by considering the transform relationships of the

individual integer decimttion and interpolation systems, the

output spectrum

Y(eiw

)

can be determined in terms

the input spectrum

X(elw)

and the frequency response of the

filter

H(ejW").

From (32) it is seen that

V(eiw")

can be ex-

pressed in terms of

X(eiw)

and

H(eiW")

J7(ei"")

H(eiw")

(ejw'IL

(50)

and from (21)

Y(eiw')

can be expressed in terms of V(eiw")as

When

H(ejW')

closely approximates the ideal characteristic

of (42) it

seen that this expression reduces to

for

lw'l

min

(a,

aM/L)

(52)

otherwise

Thus far, we have developed the general system for sampling

rate conversion of low-pass signals by arbitrary rational factors

L/M.

It was shown that the process

sampling rate conver-

sion could be modeled as a linear, periodically time-varying

system, and that the unit sample response of this system,

g,(n)

could be expressed

terms

the unit sample response

h(k)

of a time-invariant digital filter designed for the highest

system sampling rate

LF.

Sampling Rate Conversion

Bandpass Signals

In the preceding sections

was assumed that the signals

that

we are dealing with are low-pass signals and therefore the filters

-277

-H

Fig.

Decimation

a bandpass

signal

and a spectral interpretation

for

the

band.

required for decimation and interpolation are low-pass filters

which preserve the baseband signals of interest. In many

practical systems it is also necessary to deal with bandpass sig-

nals and many of the results discussed in this paper can be

logically extended to the bandpass case as well. While it is not

our intention to

into detail on these issues in this paper we

will briefly give an example in this section

one way in which

this can

done.

more involved discussion of these issues

can be found in [lo].

Perhaps the simplest and most direct approach to decimating

or interpolating digital bandpass signals is to take advantage of

the inherent frequency translating (i.e., aliasing) properties of

decimation and interpolation. This property can be used to

advantage when dealing with bandpass signals by associating

the bandpass signal with one of these modulated cLharmonics'y

instead of with the baseband. Fig. 5(a) illustrates

example

of this process for the case of decimation by the integer factor

The input signal

x(n)

is first filtered by the bandpass filter

hgp(n)

to isolate the frequency band of interest. The resulting

bandpass signal

xap(n),

then directly reduced in sampling

rate by selecting one out of every

samples giving the final

output

(m).

seen that this system

identical to that of

the integer low-pass decimator with the exception that the

fiiter

a bandpass filter instead

a low-pass filter. Thus the

output signal

Y(elW

)

can be expressed as

(53)

From (53) it is seen that

Y(ejW')

is composed

aliased

components of

X(eJW

)

HBP

(e'"')

modulated by factors of

2nllM.

The function of the filter

H~p(el~)

to remove (at-

tenuate)

all

aliasing components except those associated with

the desired band of interest. Since the modulation is restricted

306

PROCEEDINGS OF THE IEEE, VOL.

69,

NO.

MARCH

1981

to values of

2d/M

can be seen that only specific frequency

bands are allowed by this method.

a consequence the

choice

the filter

Hap

(e'")

restricted to approximate one

the

ideal characteristics

1, kn/M<IwI<(k+l)n/M

iiBp

(eiw

(54)

otherwise

where

1, i.e.,

HBP

(e'")

is restricted to

bands

kn/M

n/M

where

n/M

is the

bandwidth.

Figs. 5(b)-(e) illustrate this approach. Fig. 5(b) shows the

possible modulating frequencies which are a consequence of

the

to 1 sampling rate reduction, i.e., the digital sampling

function (a periodic train of unit samples spaced

samples

apart) has spectral components spaced

2nl/M

apart. Fig. 5(c)

shows the "sidebands" that are associated with these spectral

components which correspond to the

choices of bands as

defined by (54). They correspond to the bands that are aliased

into the baseband of the output signal

Y(ei"')

according

(54).

(As

seen by (53) and (54) and Figs. 5(b) and (c), the re-

lationship between

and

is nontrivial).

Fig. 5(d) illustrates an example in which the

band is

used, such that

X,,

(e'")

is bandlimited

the range

2n/M

3n/M.

Since the process of sampling rate reduction by

to 1 corresponds to a convolution of the spectra of

XBp

(eiw

)

(Fig. 5(d)) and the sampling function (Fig. 5fb)) this band

lowpass translated to the baseband of

Y(eiw

)

as seen in Fig.

5(e). Thus, the processes of modulation and sampling rate re-

duction are achieved simultaneously by the

to 1 sampling

rate reduction.

The process of bandpass interpolation is the inverse to that

of bandpass decimation and it can be accomplished in a similar

manner. Referring to Fig. 3(c)

is seen that we can use a

bandpass filter with a characteristic similar to that described

by (54) (with

replaced by

to remove one of the harmonic

images of the baseband signal rather than the baseband signal

itself. The net result

that we achieve both an interpolation

and a modulation

the input signal to one of its harmonic

locations in the spectrum.

III.

SIGNAL

PROCESSING

STRUCTURES

FOR

DECIMATORS

AND

INTERPOLATORS

It is easy to understand the need for studying structures for

realizing sampling rate conversion systems by examining the

simple block diagram

Fig. 4(b) which can be used to con-

vert the sampling rate of a signal by a factor of

L/M.

dis-

cussed in Section

the theoretical model for this system is

increasing the signal sampling rate by a factor of

(by filling

zero-valued samples between each sample of

x(n)

give the signal w(k)), filtering w(k)

eliminate the images

X(e'")

by a standard linear time-invariant low-pass filter,

h(k),

give

u(k),

and sampling rate compressing

u(k)

by a

factor

(by retaining 1 of each

samples of

u(k)).

direct

implementation of the system of Fig. 4(b) is grossly inefficient

since the low-pass filter

h(k)

operating at the

high

sampling

rate on a signal for which

1 out of each

input values are

zero, and the values of the filtered output are required only

once each

samples. For this example, one can directly ap-

ply this knowledge in implementing the system

Fig. 4(b) in

a more efficient manner

will be discussed in this section.

Later in Section

we will extend these concepts to include

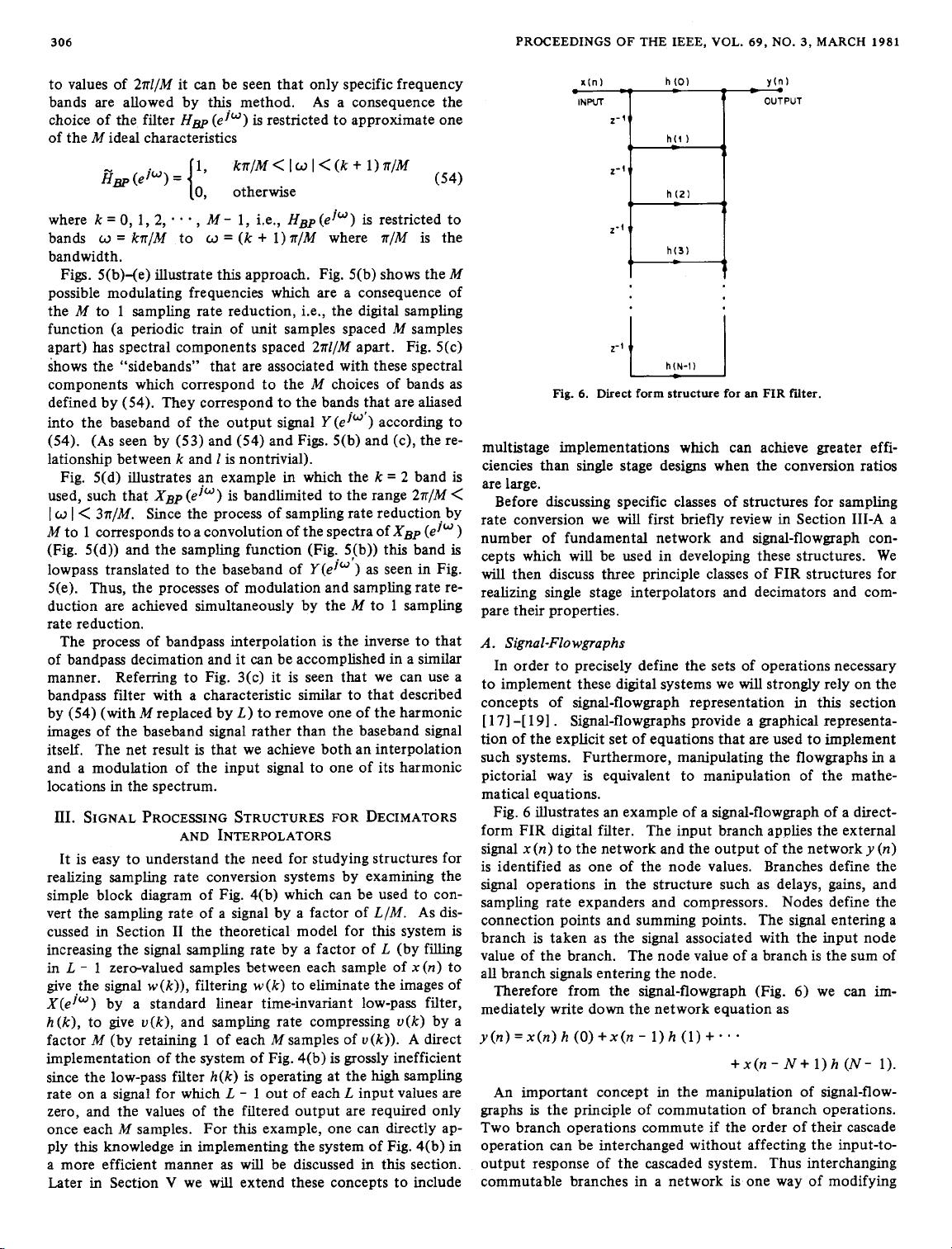
Fig.

Direct form structure for 811 FIR fdter.

multistage implementations which can achieve greater effi-

ciencies

than

single stage designs when the conversion ratios

are large.

Before discussing specific classes

structures for sampling

rate conversion we

will

first briefly review in Section 111-A a

number of fundamental network and signal-flowgraph con-

cepts which

will

be used in developing these structures. We

will

then discuss three principle classes of FIR structures for

realizing single stage interpolators and decimators and com-

pare their properties.

Signal-Flowgraphs

In order to precisely define the sets of operations necessary

to implement these digital systems we

will

strongly rely on the

concepts

signal-flowgraph representation in this section

[

171

191

Signal-flowgraphs provide a graphical representa-

tion

the explicit set of equations that are used to implement

such systems. Furthermore, manipulating the flowgraphs in a

pictorial way

equivalent to manipulation of the mathe-

matical equations.

Fig.

illustrates an example

a signal-flowgraph of a direct-

form FIR digital filter. The input branch applies the external

signal

(n)

to the network and the output of the network

(n)

is identified as one

the node values. Branches define the

signal operations in the structure such as delays, gains, and

sampling rate expanders and compressors. Nodes define the

connection points and summing points. The signal entering a

branch is taken as the signal associated with the input node

value of the branch. The node value of a branch is the sum of

all branch signals entering the node.

Therefore from the signal-flowgraph (Fig.

we can im-

mediately write down the network equation as

y(n)

=x(n)

(0)

+x(n

(1)

+x(n

N+

1)h

(N-

1).

An important concept

the manipulation

signal-flow-

graphs

the principle of commutation of branch operations.

Two branch operations commute if the order of their cascade

operation can be interchanged without affecting the input-to-

output response of the cascaded system. Thus interchanging

commutable branches in a network

one way of modifying

剩余31页未读，继续阅读

Phirix

粉丝: 0
资源: 2

数字信号处理：插值与降采样教程

An economical class of digital filters for decimation and interpolation

Optimum FIR Digital Filter Implementations for Decimation, Interpolation

A Study of Spatial Color Interpolation Algorithms for Digital Cameras

RBF Interpolation and Approximation.ppt

Interpolation in Digital Modems-Part II Implementation and Performance

Data-Driven Shape Interpolation and Morphing Editing

NeuroMorph Unsupervised Shape Interpolation and Corresponden.pdf

Interpolation and approximation by rational functions in the complex domain

A color interpolation algorithm for Bayer pattern digital cameras

Interpolation in digital Modems_ part I

最新资源