利用联树嵌入计算三正则图曲面嵌入亏格分布

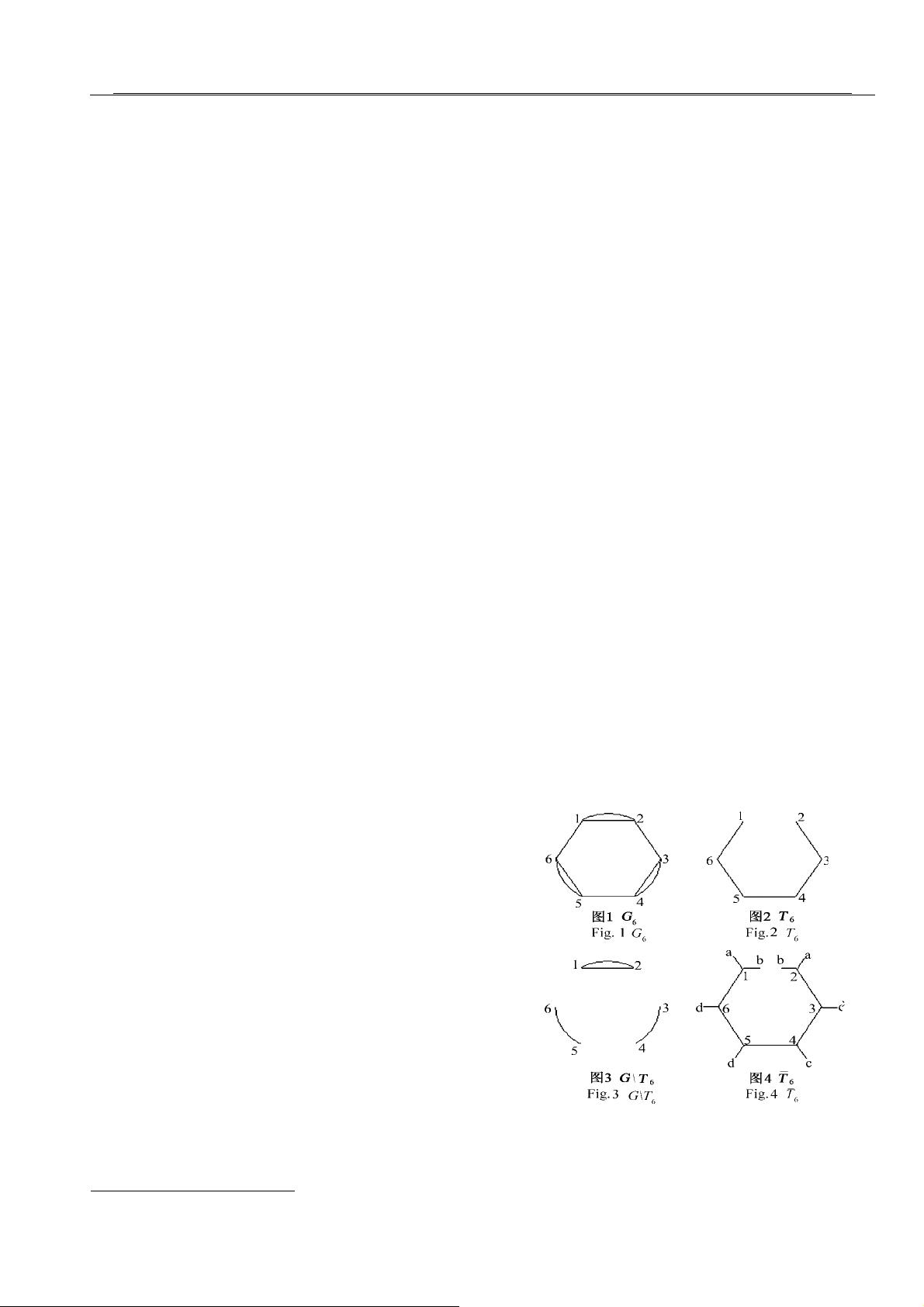
"一类三正则图的嵌入亏格分布 (2004年) - 图的嵌入亏格分布的计算方法通过联树嵌入的理论，由李立峰和刘彦佩提出，适用于三正则图" 图的嵌入亏格分布是图论中的一个重要概念，它涉及图在各种曲面（包括可定向和不可定向的）上的嵌入方式。在这个领域，亏格是衡量曲面复杂度的一个关键参数，对于理解图的结构和性质至关重要。在2004年的一篇论文中，李立峰和刘彦佩探讨了如何计算一类三正则图的曲面嵌入亏格分布。 三正则图指的是每条边连接两个不同的顶点，且每个顶点都有恰好三条边连接的图。这些图在数学上有着丰富的结构，它们的嵌入问题可以提供关于图的几何和拓扑信息。论文中，作者利用了联树嵌入的方法，这是一种处理图嵌入的有效工具，它通过构建树状结构来分析图在曲面上的排列。 联树嵌入方法的核心是将复杂的图分解为更简单的树结构，然后研究这些树如何在曲面上排列。在本研究中，联树的概念帮助作者将三正则图的嵌入问题转化为更易于处理的形式。同时，刘彦佩的理论提供了关键的理论框架，使得计算嵌入亏格分布成为可能。 论文中提到的“嵌入多项式”是一种表示图的所有可能嵌入方式及其对应亏格的数学工具。这个多项式可以揭示图在不同曲面上嵌入的可能性和概率，从而帮助我们理解图的拓扑特性。通过这个公式，研究人员能够系统地计算特定类型三正则图在各种曲面上的嵌入亏格分布。 在实际应用中，理解图的嵌入亏格分布对于网络设计、编码理论和计算复杂性等领域具有重要意义。例如，在计算机科学中，图的嵌入可以映射到数据结构的设计，而嵌入亏格分布则可以提供关于这些结构在不同计算环境下的效率和稳定性的信息。 这篇论文的贡献在于提供了一个计算特定类三正则图嵌入亏格分布的公式，这不仅加深了我们对这类图的理解，也为相关领域的研究提供了有力的理论支持。作者通过严谨的数学方法和创新的思路，解决了图论中的一个具体问题，展示了图论与曲面拓扑的紧密联系。