MATLAB绘制二元函数图形及等高线教程

"MATLAB绘制二元函数图形的教程" 在MATLAB中绘制二元函数的图形是一项基础且重要的技能，这对于理解和分析多变量函数的行为至关重要。本教程详细介绍了如何使用MATLAB来绘制二元函数的图形，包括空间曲面和等高线。 首先，我们关注实验的目的。实验目标是让学生理解并掌握二元函数图形的绘制，空间曲面的等高线表示，以及多元函数的插值方法。同时，通过实践操作，学生能熟练运用MATLAB的相关绘图命令。 实验中涉及到的关键命令有`mesh`和`surf`。`mesh`命令用于绘制网格曲面，它需要三个数据矩阵——`x`、`y`和`z`，分别代表数据点的横坐标、纵坐标和对应的函数值。此命令将这些数据点连接起来形成一个网格形状。而`surf`命令则用于绘制完整的曲面，同样需要`x`、`y`和`z`矩阵，但它会填充曲面，使其更具视觉效果。 实验的重点在于二元函数的描点法，即如何根据函数解析式生成坐标点并连接成图；其次，曲面交线的计算也是一项关键技能，这通常涉及到求解两个或多个函数方程的交集。最后，生成地形图的过程也是实验的一部分，这需要理解如何利用函数值来模拟地势起伏。 实验难点主要包括上述的二元函数图形的描点法和曲面交线的计算，这两点需要对函数和几何有一定的理解才能准确实现。 实验步骤以绘制函数`z = x^2 + y^2`为例，代码如下： 1. 清除内存：`>> clear;` 2. 定义`x`和`y`的范围：`>> x = -3:0.1:3;` `>> y = -3:0.1:3;` 3. 使用`meshgrid`将`x`和`y`转换为矩阵`X`和`Y`：`>> [X,Y] = meshgrid(x,y);` 4. 计算`z`值：`>> Z = sqrt(X.^2+Y.^2);` 5. 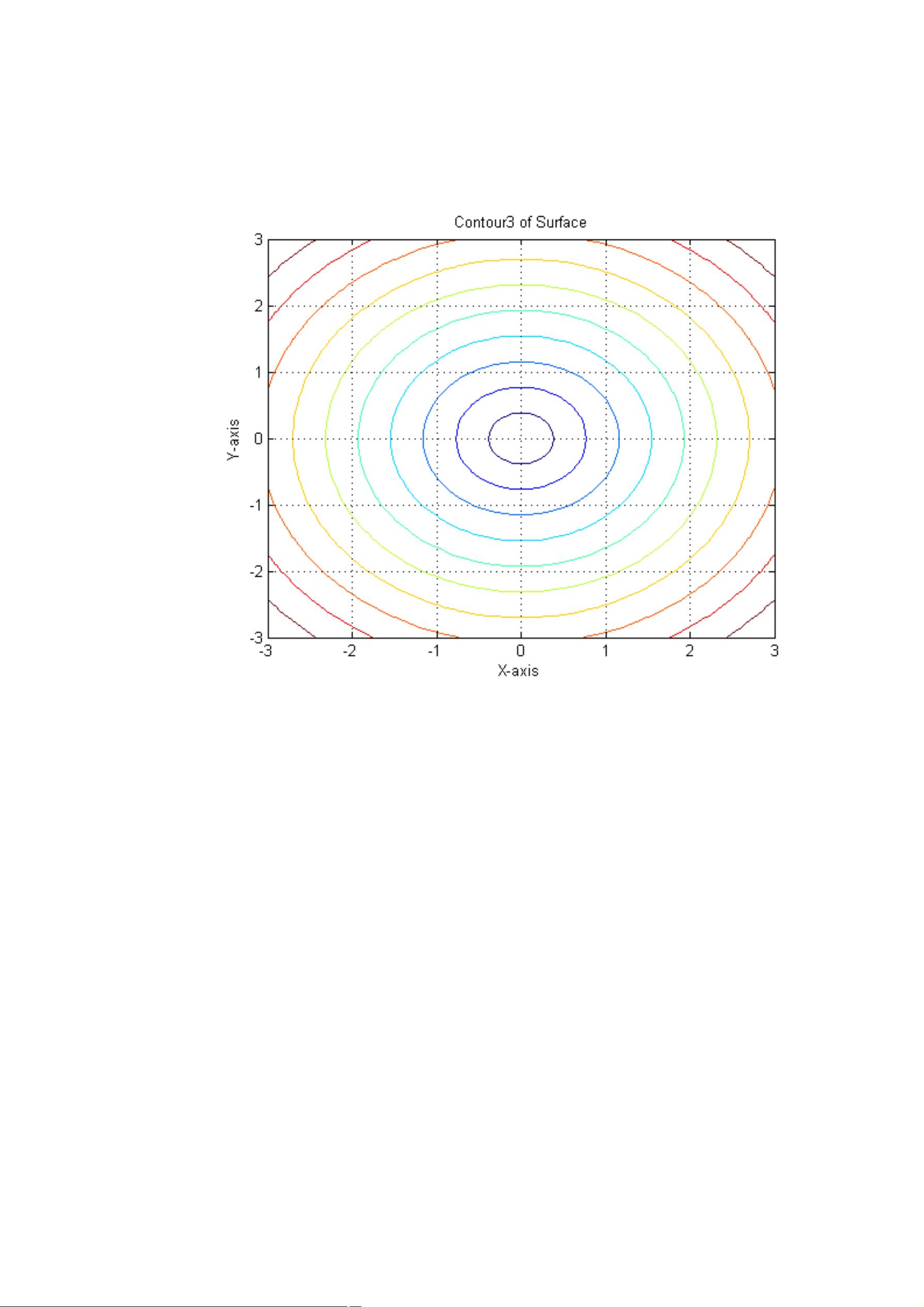使用`mesh`绘制图形：`>> mesh(X,Y,Z);` 如果要画等高线，可以使用`contour`或`contour3`命令。例如，要画10条等高线，代码如下： 1. 绘制三维等高线：`>> contour3(X,Y,Z,10);` 2. 添加坐标轴标签：`>> xlabel('X-axis'), ylabel('Y-axis'), zlabel('Z-axis');` 3. 设置图形标题：`>> title('Contour3 of Surface');` 4. 显示网格线：`>> grid on;` 若要绘制二维等高线，只需去掉`contour3`中的"3"即可，其他部分保持不变。 通过这样的练习，学生能够深入理解二元函数图形的特性，提升在MATLAB中的可视化能力，这对于科学计算和数据分析工作大有裨益。