计算几何入门：算法详解与实战技巧

"该资源是一份详细的计算几何学习材料，由ACFightersXZZ于2008年12月30日分享。内容涵盖了计算几何的基础知识、特点、应用场景以及解题技巧，并特别强调了处理浮点数比较、算法优化和特定几何问题的解决方法。" 计算几何是计算机科学的一个分支，它专注于开发解决几何问题的算法。这个领域在图形学、机器人技术、集成电路设计和统计等多个现代工程和数学领域中具有广泛应用。计算几何的特点包括其知识点相对独立，与其他领域的交集较少，同时题目通常具有大代码量、多种特殊情况、精度控制困难以及对几何和三角函数的精通要求。在编程竞赛中，计算几何题目虽然难度适中，但并不容易。 面对计算几何中的各种问题，需要注意以下几点： 1. 不要用`==`直接判断浮点数相等，因为浮点数的精度问题可能导致错误。可以使用一个极小的误差阈值（如`EPS=1e-9`）进行近似比较，例如`fabs(x-y)<EPS`用于判断浮点数相等，`fabs(x)<EPS`判断浮点数是否接近零。 2. 在处理浮点数时，尽量避免除法，尤其是除以小数，可以通过适当放大转换为整数运算，然后再转换回浮点数。 3. 避免两个非常接近的数相减，这可能导致精度损失。在编写算法时，考虑使用加法和乘法代替减法。 4. 当涉及到数学函数时，如需要用到开方或三角函数，确保包含`<math.h>`头文件，以避免因缺少定义而导致的错误。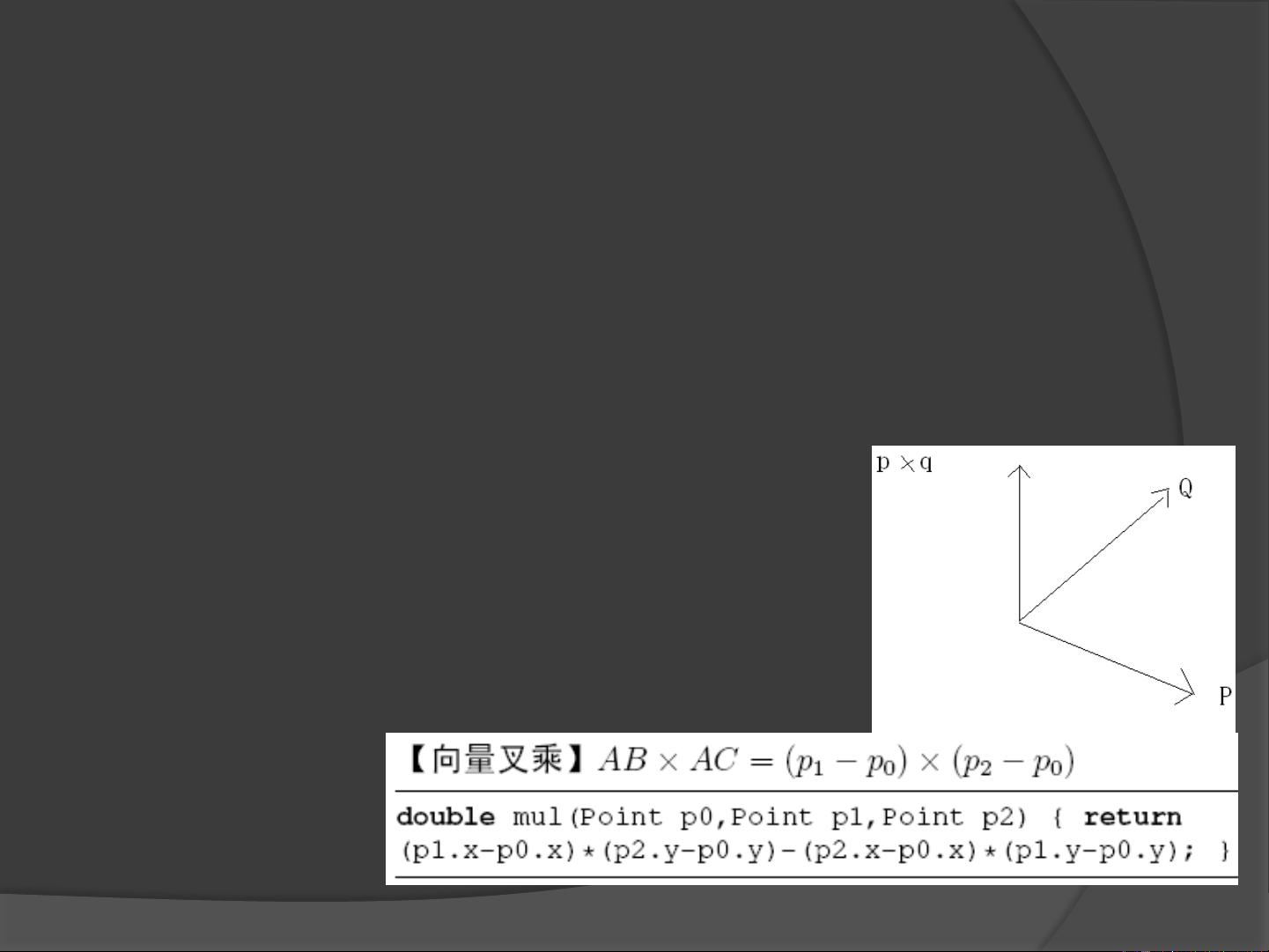 学习计算几何，可以从基础概念开始，如叉积和点积，它们是处理直线、线段和点之间关系的关键。叉积可以确定两个向量在二维空间中的旋转方向，用于判断直线和线段的相对位置。点积可用于计算向量的投影和判断向量的平行或垂直关系。 此外，文档中还提到了与矩形相关的包含问题，如判断点是否在矩形内，这是几何算法中的基本问题。点在多边形内的判断方法也是计算几何中的常见知识点。同时，线段在多边形内的判断和离散化技术，如将连续区间转换为离散点集，有助于简化问题。凸包算法，如Graham-Scan算法，是计算几何中的一个重要工具，用于找到一组点的最小外接凸多边形。 这份资料提供了计算几何的基本知识和实用技巧，适合初学者入门和提高。通过深入学习这些概念和方法，开发者能够更好地解决实际中的几何计算问题。