探索卷积神经网络的深度解析：滤波器、步幅与创新卷积技术

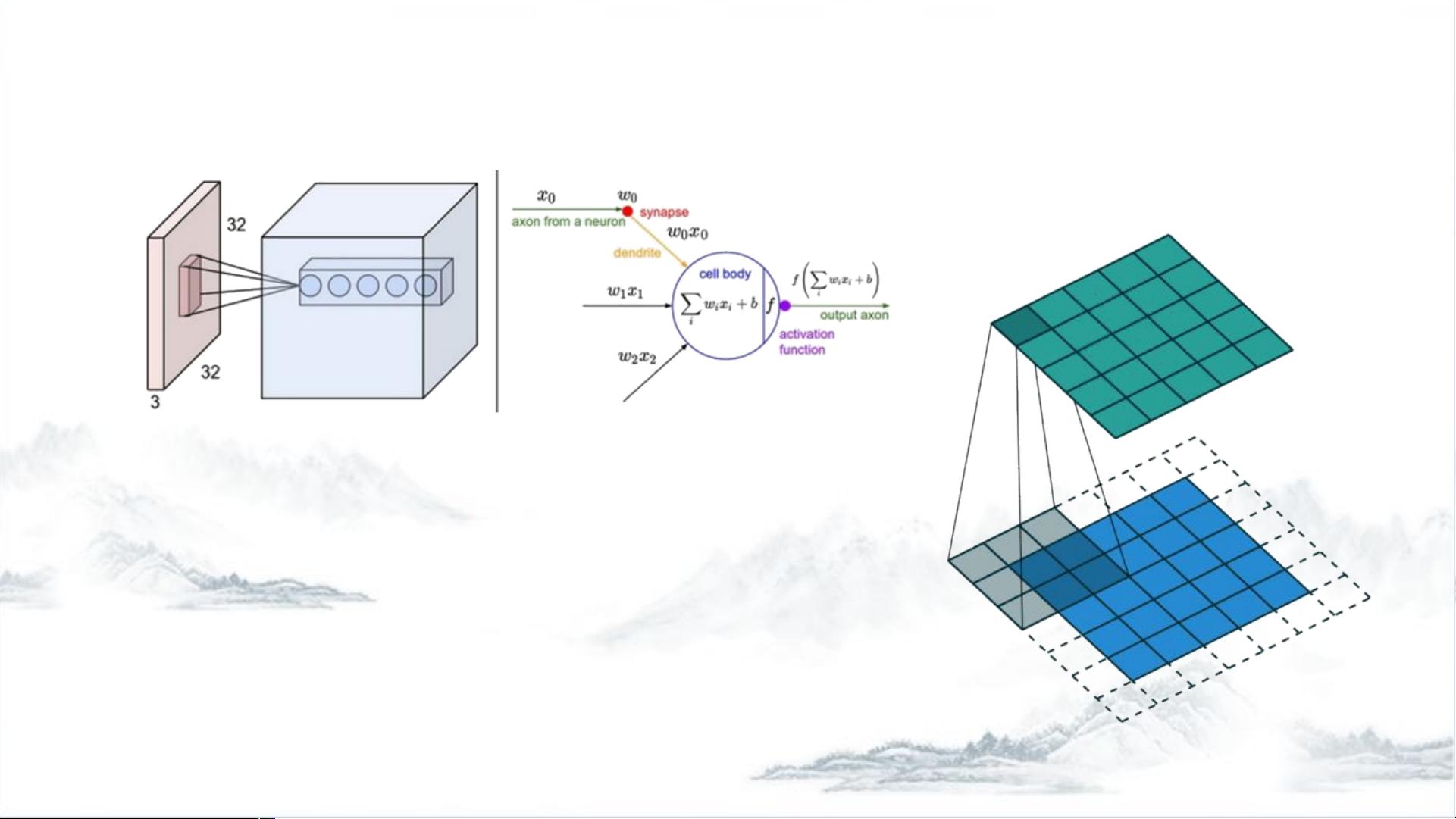
卷积神经网络（Convolutional Neural Networks, CNNs）是一种深度学习模型，特别适用于处理具有网格结构的数据，如图像和视频。本篇文章将详细介绍CNN的核心组件——卷积层，以及一些重要的改进版本，包括转置卷积、空洞卷积、可变形卷积和3D卷积。 卷积层是CNN的基础，其核心在于局部连接和权值共享。卷积核（kernels）是关键组件，其大小（Kernel Size, k）决定了卷积层的视野范围，也就是每个神经元接收到输入数据的局部特征。步幅（Stride, S）控制了卷积核在图像上移动的间隔，若步幅为1，则每次移动一个像素，这会影响输出特征图的大小。边界处理（Padding）用于保持输出特征图与输入数据相同的尺寸，通过在边缘添加0（Zero-padding）实现，这是一项重要的超参数。 卷积层的特点是深度方向上的连接固定与输入数据的深度相同，而在空间维度（宽度和高度）上则是局部连接。输出通道数（Output Channels, n）决定了输出特征图的深度，每个通道代表不同的特征检测。输出数据体的尺寸可以通过公式 (W-F+2P)/S+1计算，其中W是输入尺寸，F是卷积核尺寸，P是填充大小，S是步幅。 转置卷积（Transposed Convolution 或 Deconvolution）是反向操作于卷积，常用于上采样或降维后的特征图恢复，如在生成对抗网络（GANs）中的DCGAN（Deep Convolutional Generative Adversarial Networks）和U-net中。它允许将低分辨率特征映射回原始尺寸，但要注意的是，转置卷积的输入和输出尺寸、步幅以及填充的选择对结果有直接影响。 空洞卷积（Dilated Convolution）是一种扩展卷积的方式，通过在卷积核中引入空洞（dilation），增加了神经元的视野，但不会增加计算成本。这样做有助于在保留特征上下文的同时减小参数数量，对于长距离依赖关系的捕捉非常有用。 可变形卷积（Deformable Convolution）是一种更具灵活性的卷积形式，允许卷积核在位置上有一定程度的调整，增强了模型对输入数据中的物体变形和扭曲的适应性。 3D卷积（3D Convolution）则是对传统2D卷积的扩展，适用于处理具有三维结构的数据，例如视频帧序列，它在时空维度上同时进行卷积。 理解并掌握这些卷积层的特性及其改进版本对于深入理解和应用CNN在图像处理、计算机视觉和其他相关领域至关重要。通过优化这些参数和设计，我们可以构建出更高效、更具适应性的卷积神经网络模型。