计算机图形学：直线的扫描转换算法

"Chapter 3 基本图元算法主要介绍了如何在计算机图形学中生成和显示基本的二维几何图形，如点、直线、圆、椭圆、多边形和字符串等。其中，重点关注了直线的扫描转换算法——数值微分法（DDA法）。" 在计算机图形学中，基本图元的生成算法是一个关键环节，因为它涉及到如何在指定的输出设备上根据坐标精确地描绘这些图形。这些图形包括但不限于点、直线、圆、椭圆、多边形和文字，以及它们的相关属性，如颜色、亮度和线宽。光栅化是将这些图形转化为显示器能够理解的像素表示的过程。 一个简单的二维图形显示流程通常包括扫描转换阶段。在这个阶段，图形的顶点由用户定义，并通过某种算法转换成像素阵列，最终在光栅显示系统上呈现出来。以直线为例，生成直线的基本要求是要保证其在屏幕上连续、粗细均匀且亮度一致，通过像素逼近来实现。为了快速并准确地绘制直线，扫描转换算法至关重要。 扫描转换的主要任务是找到最接近原始图形的像素集合，这通常通过确定每个像素的位置并赋予相应的颜色或属性来完成。对于直线来说，DDA（差分下降算法）是一种常用的方法。DDA利用直线的微分方程来计算每个像素点的位置，确保直线的连续性和平滑性。它的工作原理是通过不断迭代，每次增加一个单位的x值，根据斜率k更新y值，然后将像素点绘制在屏幕上。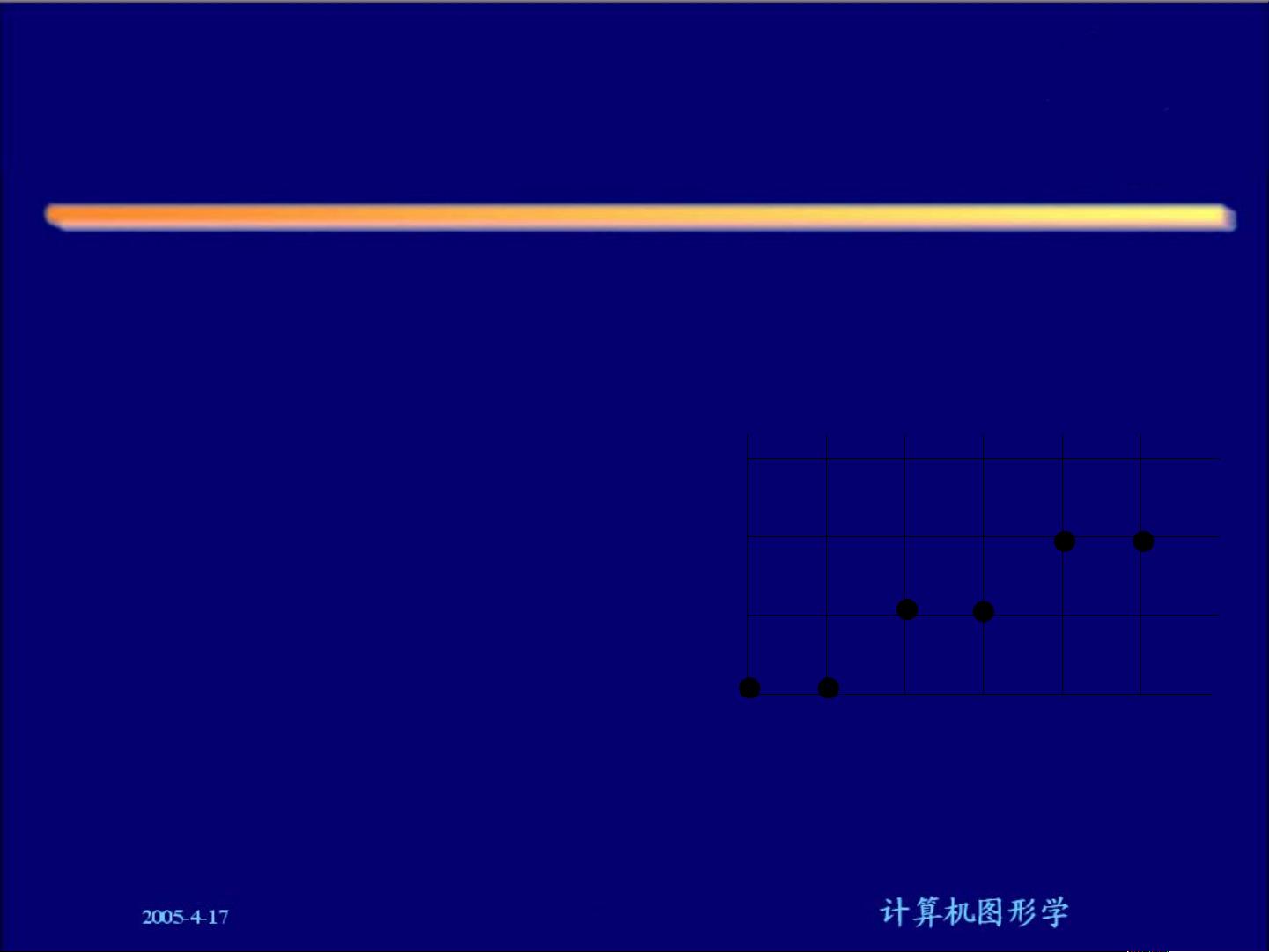 具体到DDA算法，假设直线的两个端点分别为P0(x0, y0)和P1(x1, y1)，通过计算直线的斜率k，可以得出x每增加1，y应增加的值。在实际编程中，通常会使用for循环来遍历x值，每次迭代时，计算对应的y值并四舍五入到最近的整数，然后在屏幕上画出像素点。例如，画一条从(0,0)到(5,2)的直线，会按顺序画出一系列的像素点，确保直线的平滑显示。 基本图元的生成算法是计算机图形学中的基础，而扫描转换和DDA算法是实现这一过程的关键技术，它们使得我们能够在屏幕上有效地渲染出各种复杂的图形。理解并掌握这些概念和技术对于深入学习计算机图形学和相关领域至关重要。