It has been observed that these implicit filters are closely
related to the explicit ones. In [43], Elad shows that the
bilateral filter is one Jacobi iteration in solving the Gaussian
affinity matrix. The Hierarchical Local Adaptive Precondi-
tioners [41] and the Edge-Avoiding W avelets [37] are
constructed in a similar manner. In this paper, we show
that the guided filter is closely related to the matting
Laplacian matrix [10].
2.3 Nonaverage Filters
Edge-preserving filtering can also be achieved by nonaver-
age filters. The median filter [2] is a well-known edge-aware
operator, and is a special case of local histogram filters [44].
Histogram filters have Oð NÞ time implementations in a way
as the bilateral grid. The Total-Variation (TV) filters [45]
optimize an L
1
-regularized cost function, and are shown
equivalent to iterative median filtering [46]. The L
1
cost
function can also be optimized via half-quadratic split [47],
alternating between a quadratic model and soft shrinkage
(thresholding). Recently, Paris et al. [48] proposed manip-
ulating the coefficients of the Laplacian Pyramid around
each pixel for edge-aware filtering. Xu et al. [49] propose
optimizing an L
0
-regularized cost function favoring piece-
wise constant solutions. The nonaverage filters are often
computationally expensive.
3GUIDED FILTER
We first define a general linear translation-variant filtering
process, which involves a guidance image I, an filtering
input image p, and an output image q. Both I and p are
given beforehand according to the application, and they can
be identical. The filtering output at a pixel i is expressed as
a weighted average:
q
i
¼
X
j
W
ij
ðIÞp
j
; ð1Þ
where i and j are pixel indexes. The filter kernel W
ij
is a
function of the guidance image I and independent of p. This
filter is linear with respect to p.
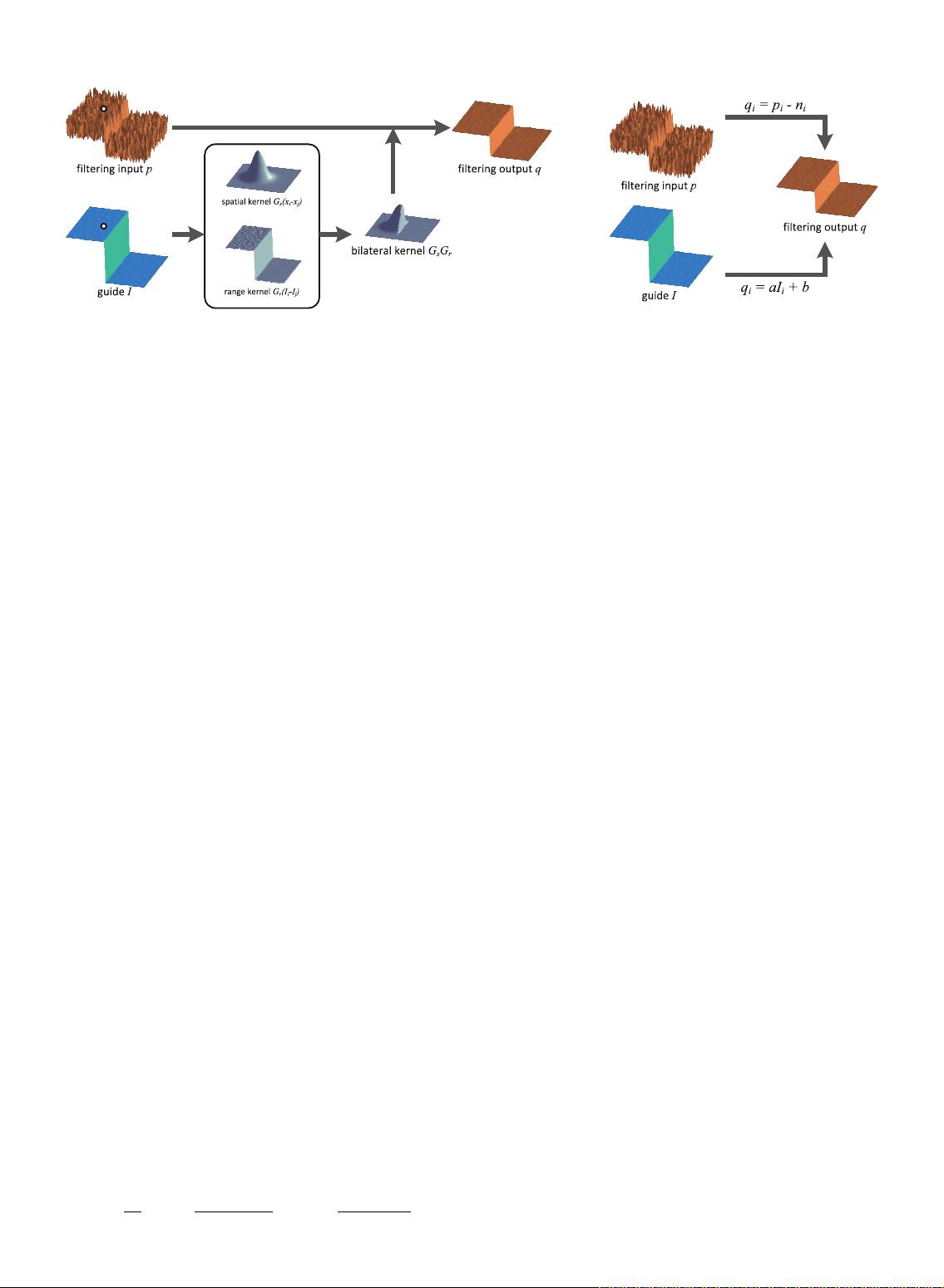
An example of such a filter is the joint bilateral filter [14]
(Fig. 1 (left)). The bilateral filtering kernel W
bf
is given by
W
bf
ij
ðIÞ¼
1
K
i
exp
k x
i
x
j
k
2
2
s
exp
k I
i
I
j
k
2
2
r
; ð2Þ
where x is the pixel coordinate and K
i
is a normalizing
parameter to ensure that
P
j
W
bf
ij
¼ 1. The parameters
s
and
r
adjust the sensitivity of the spatial similarity and the
range (intensity/color) similarity, respectively. The joint
bilateral filter degrades to the original bilateral filter [1]
when I and p are identical.
The implicit weighted-average filters (in Section 2.2)
optimize a quadratic function and solve a linear system in
this form:
Aq ¼ p; ð3Þ
where q and p are N-by-1 vectors concatenating fq
i
g and
fp
i
g, respectively, and A is an N-by-N matrix only depends
on I. The solution to (3), i.e., q ¼ A
1
p, has the same form as
(1), with W
ij
¼ðA
1
Þ
ij
.
3.1 Definition
Now we define the guided filter. The key assumption of the
guided filter is a local linear model between the guidance I
and the filtering output q. We assume that q is a linear
transform of I in a window !
k
centered at the pixel k:
q
i
¼ a
k
I
i
þ b
k
; 8i 2 !
k
; ð4Þ
where ða
k
;b
k
Þ are some linear coefficients assumed to be
constant in !
k
. We use a square window of a radius r. This
local linear model ensures that q has an edge only if I has an
edge, because rq ¼ arI. This model has been proven
useful in image super-resolution [50], image matting [10],
and dehazing [11].
To determine the linear coefficients ða
k
;b
k
Þ, we need
constraints from the filtering input p. We model the output q
as the input p subtracting some unwanted components n
like noise/textures:
q
i
¼ p
i
n
i
: ð5Þ
We seek a solution that minimizes the difference between q
and p while maintaining the linear model (4). Specifically,
we minimize the following cost function in the window !
k
:
Eða
k
;b
k
Þ¼
X
i2!
k
a
k
I
i
þ b
k
p
i
2
þ a
2
k
: ð6Þ
Here, is a regularization parameter penalizing large a
k
.We
will investigate its i ntuitive meaning in Section 3.2.
Equation (6) is the linear ridge regression model [51], [52]
and its solution is given by
HE ET AL.: GUIDED IMAGE FILTERING 1399
Fig. 1. Illustrations of the bilateral filtering process (left) and the guided filtering process (right).









