数据建模实战:泰坦尼克号线性模型分类解析
版权申诉
100 浏览量
更新于2024-06-26
1
收藏 2.87MB PDF 举报
"深度学习项目开发实战_数据建模实战-泰坦尼克号示例_编程案例解析实例详解课程教程.pdf"
在数据科学领域,线性模型是基础且至关重要的学习算法,尤其对于初学者而言,理解其原理是掌握更复杂算法,如深度学习和神经网络的基石。"泰坦尼克号"示例是一个经典的数据建模问题,通过这个案例,我们可以学习如何运用线性模型进行分类任务,了解从数据预处理、探索到模型构建和评估的全过程。
首先,线性回归模型是回归分析的基础,它的主要任务是预测连续数值型的输出变量。在最简单的形式中,线性回归方程描述了输入变量(自变量)x与输出变量(因变量)y之间的线性关系,即y = c + bx,其中c是截距,b是斜率或系数,表示x每增加一个单位,y预期的变化量。线性回归模型关注的是输入变量对输出变量的影响程度以及这种影响的方向。
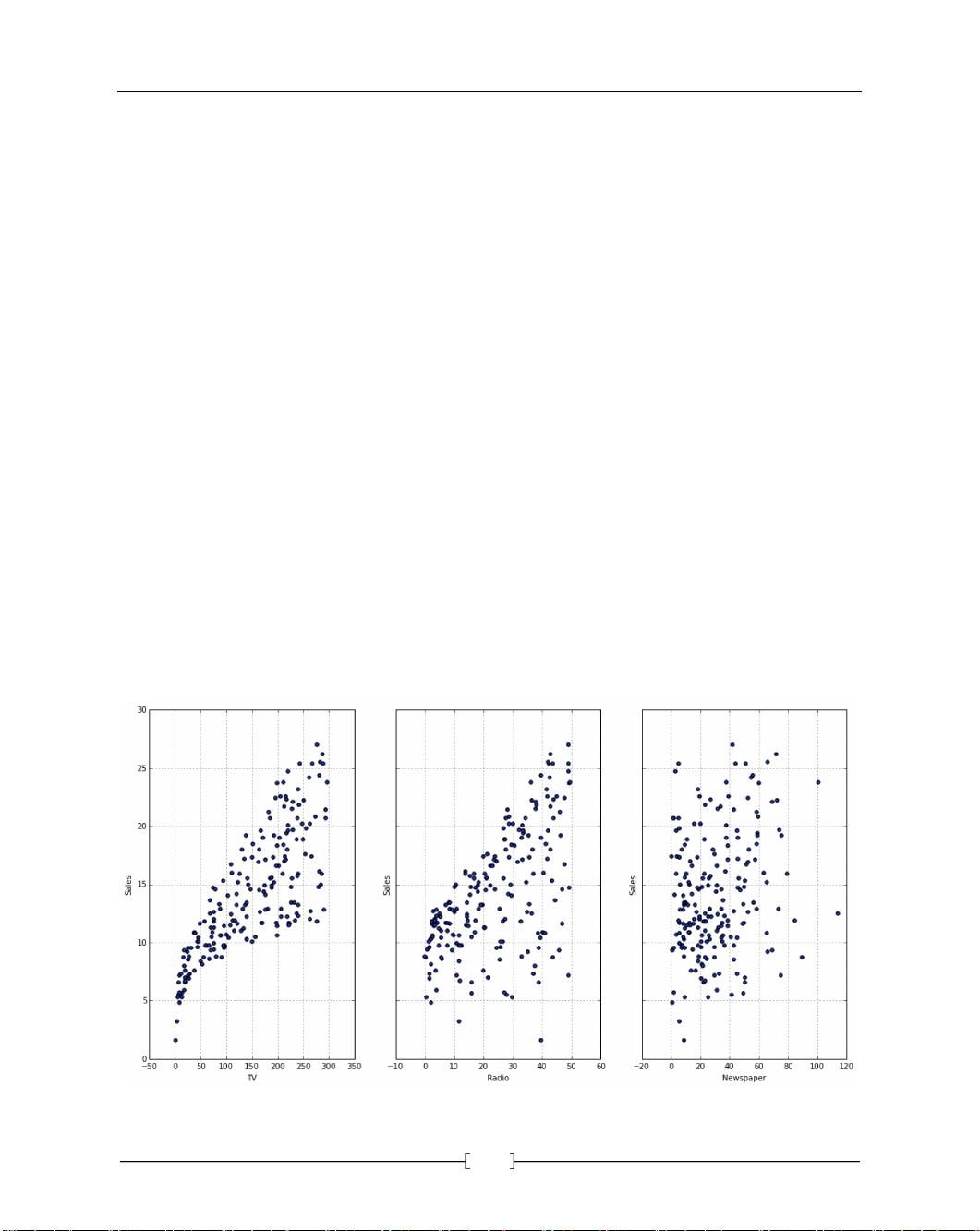
然后,线性模型也常被用于分类任务,这被称为逻辑回归或线性分类模型。在分类中,线性模型通过sigmoid或其他函数将连续的预测值转换为离散的类别概率。例如,在泰坦尼克号的问题中,可能需要预测乘客生还的概率,线性模型可以用来估计各特征(如年龄、性别、船票价格等)对生存概率的影响。
在"泰坦尼克号"示例中,我们将学习如何处理和探索数据,包括缺失值的填充、异常值的处理、特征工程等步骤。接着,我们会构建和训练线性模型,通过训练集来拟合模型参数,并在验证集或测试集上评估模型的性能。这通常涉及到选择合适的性能指标,如准确率、精确率、召回率或F1分数。
此外,线性模型因其简单性而受到欢迎。它们运行速度快,不需要大量的计算资源,且易于理解和解释。线性回归模型的参数直接对应于特征的重要性,使得模型的决策过程清晰易懂。这对于模型的解释和传达给非技术团队是非常有价值的。尽管线性模型可能在某些复杂问题上表现不如非线性模型,但它们往往是初步探索和快速原型设计的良好起点,因为它们通常不需要大量的参数调整。
最后,线性模型也是其他更复杂模型的基础,比如多项式回归、岭回归和Lasso回归,这些模型通过扩展线性模型的能力来适应更复杂的数据结构。通过学习和理解线性模型,我们可以为后续学习更高级的机器学习技术打下坚实的基础。
2018-12-14 上传
2020-04-17 上传
2023-09-03 上传
2023-08-17 上传
2023-08-20 上传
2023-06-06 上传
2024-11-13 上传
2023-07-27 上传
好知识传播者
- 粉丝: 1679
- 资源: 4133
最新资源
- mobile-cloud-ios-technician:带有用于移动设备的SAP Cloud SDK的示例iOS应用程序,向服务技术人员展示了查看其服务订单,产品和客户以及在移动设备上使用数据的情况
- SDLx-Betweener:Perl补间库
- Ctrl_GraphWindow:C#实时用户可配置的图表控件-开源
- gulp-file-wrapper:将文件内容包装在另一个文件中的 gulp 插件
- 电信设备-一种基于图像采样线灰度信息分析的一维条码识别方法.zip
- 实现拖动的模糊效果视图效果
- jQuery自定义标签选项卡插件特效代码
- labatorio_2
- TabCorral-crx插件
- backboneStart:使用主干开发前端的入门包 + 需要使用 bower 依赖安装程序
- MapNoReduce:没有还原阶段的C#分布式映射
- puppet-java-service-wrapper:安装Java-service-wrapper库的木偶模块
- 最新大气时尚素材资源下载站模版源码,FE素材网
- jQuery基于Bootstrap分页插件特效代码
- wordcount_project:Django Web应用程序
- STM32之PWM驱动LED呼吸灯