Java实现香农编码与信源熵计算

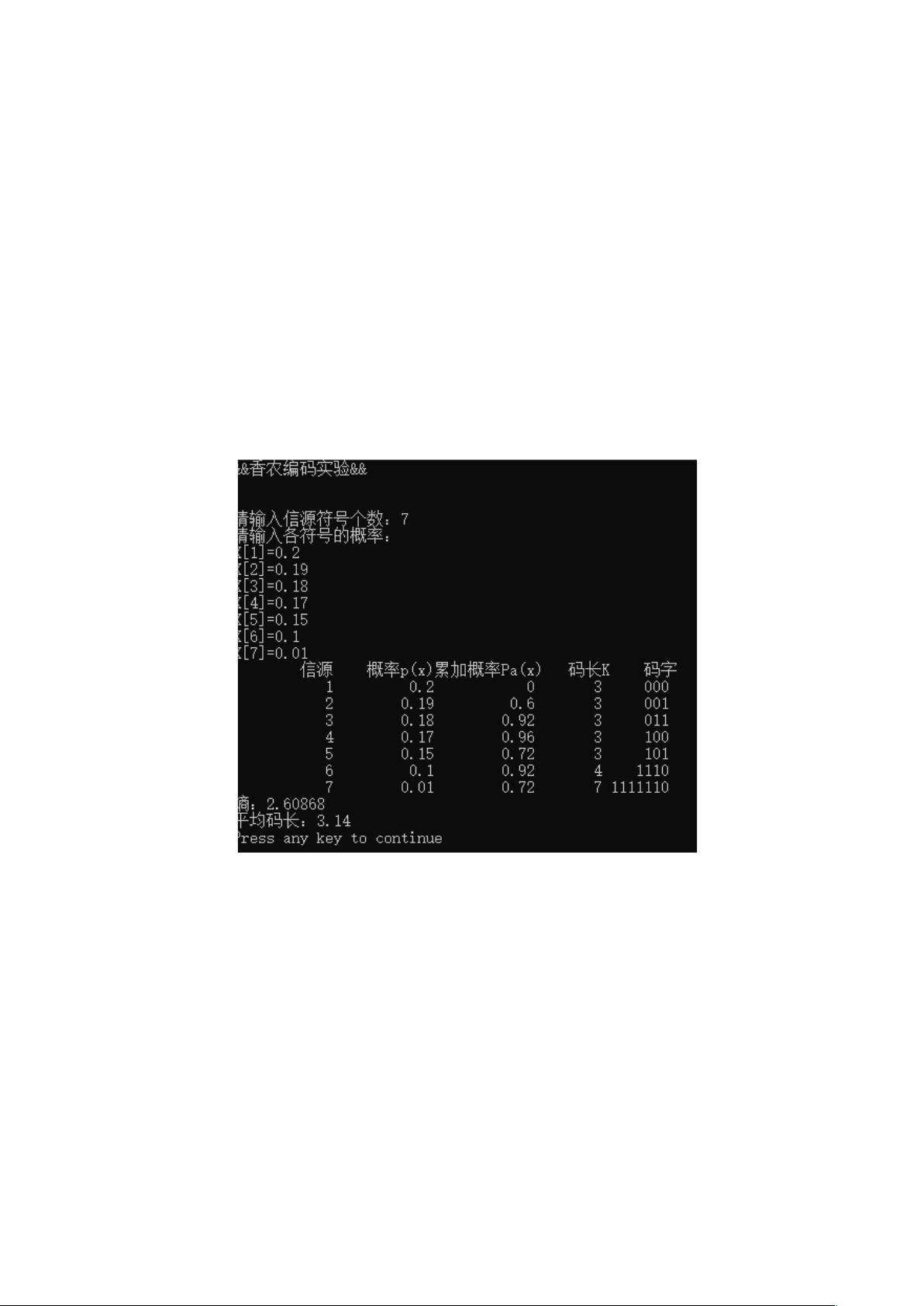
"Java 实现香农编码，信息论中的编码算法" 在信息论中，香农编码是一种无损数据压缩方法，由克劳德·香农提出，旨在利用符号出现的概率来创建一种编码方式，使得高概率符号的编码长度较短，低概率符号的编码长度较长。这一编码策略有助于在保持数据完整性的同时，有效压缩信息，提高编码效率。香农编码是信息论中的三大译码准则之一，其目标是使编码的平均码长接近信源熵，以达到最佳压缩效果。 在给定的描述中，任务要求使用Java实现香农编码算法，具体实现D=2的情况，即考虑两种可能的输入符号。上机内容包括实现编码算法，计算平均码长、信源熵以及编码效率，并可选地检查输入数据的合法性，如概率值是否为1。 提供的源代码部分是一个名为`Shannon`的类，其中包含一个内部类`Date`。`Date`类用于存储每个符号的编码、概率、长度和累积概率。`createDate()`方法用于获取用户输入的信源符号和概率，`setcode()`和`setProb()`方法分别设置符号和概率。然而，完整的代码实现还包括计算编码、平均码长、信源熵和编码效率的逻辑，这部分在给出的代码中未提供。 为了完成这个任务，我们需要以下步骤： 1. **计算累积概率**：根据输入的各符号概率，累计概率，确保概率之和为1。 2. **分配编码**：按照香农编码的规则，从最小累积概率开始，分配最短的二进制码，然后按顺序增加码长。 3. **计算平均码长**：使用计算出的编码，乘以对应符号的概率，再求和，得到平均码长。 4. **计算信源熵**：信源熵H(X)是所有符号概率的负对数的加权平均，公式为`H(X) = - ∑(p_i * log2(p_i))`，其中p_i是第i个符号的概率。 5. **计算编码效率**：编码效率是信源熵与平均码长的比值，表示编码的实际效果。 完整的`Shannon`类应包含处理这些计算的方法，并提供主函数来运行整个流程。同时，可以添加输入验证以确保概率值在0到1之间，且总和为1。 例如，可以添加以下方法： ```java public void calculateCoding() { // 按照累积概率分配编码 // ... } public double calculateAverageCodeLength() { // 计算平均码长 // ... } public double calculateEntropy() { // 计算信源熵 // ... } public double calculateCodingEfficiency() { // 计算编码效率 // ... } public static void main(String[] args) { Shannon shannon = new Shannon(); shannon.createDate(); shannon.calculateCoding(); double avgCodeLength = shannon.calculateAverageCodeLength(); double entropy = shannon.calculateEntropy(); double efficiency = shannon.calculateCodingEfficiency(); System.out.println("平均码长: " + avgCodeLength); System.out.println("信源熵: " + entropy); System.out.println("编码效率: " + efficiency); } ``` 请注意，完整的`calculateCoding()`方法需要实现香农编码的具体逻辑，这通常涉及到排序和码长的分配。在实际应用中，可能会使用数据结构如优先队列或平衡树来高效地进行这些操作。 最后，记得将运行结果保存并上传到指定的FTP服务器。这是一个涉及信息论、编码理论和Java编程的实际问题，通过解决它可以深入理解香农编码及其在数据压缩中的作用。