C++实现Floyd算法解决所有顶点间最短路径

本文主要介绍了如何在C++中使用Floyd算法来计算有向图中所有顶点之间的最短路径。Floyd算法，也称为Floyd-Warshall算法，是一种动态规划方法，特别适合于解决带有负权边但不存在负权重环的问题。它的核心思想是通过比较当前路径和经过中间顶点的路径，不断更新每对顶点之间的最短距离。 算法的基本流程如下： 1. **前提条件**：图中不允许存在负权值的边，因为负权值可能导致无限循环，使得算法无法正确求解最短路径。 2. **时间复杂度**：Floyd算法的时间复杂度是O(n^3)，其中n是图中顶点的数量。这是因为算法需要遍历所有可能的中间顶点k来检查是否存在更短的路径。 3. **迭代过程**： - 从k=0到k=n-1进行k次迭代，对于每一对顶点(i, j)： a. 检查是否可以通过中间顶点k找到更短的路径，即dist[i][k] + dist[k][j] < dist[i][j]。 b. 如果满足条件，更新dist[i][j]的值为新路径的长度，并更新path[i][j]指向最优路径上通过k的顶点。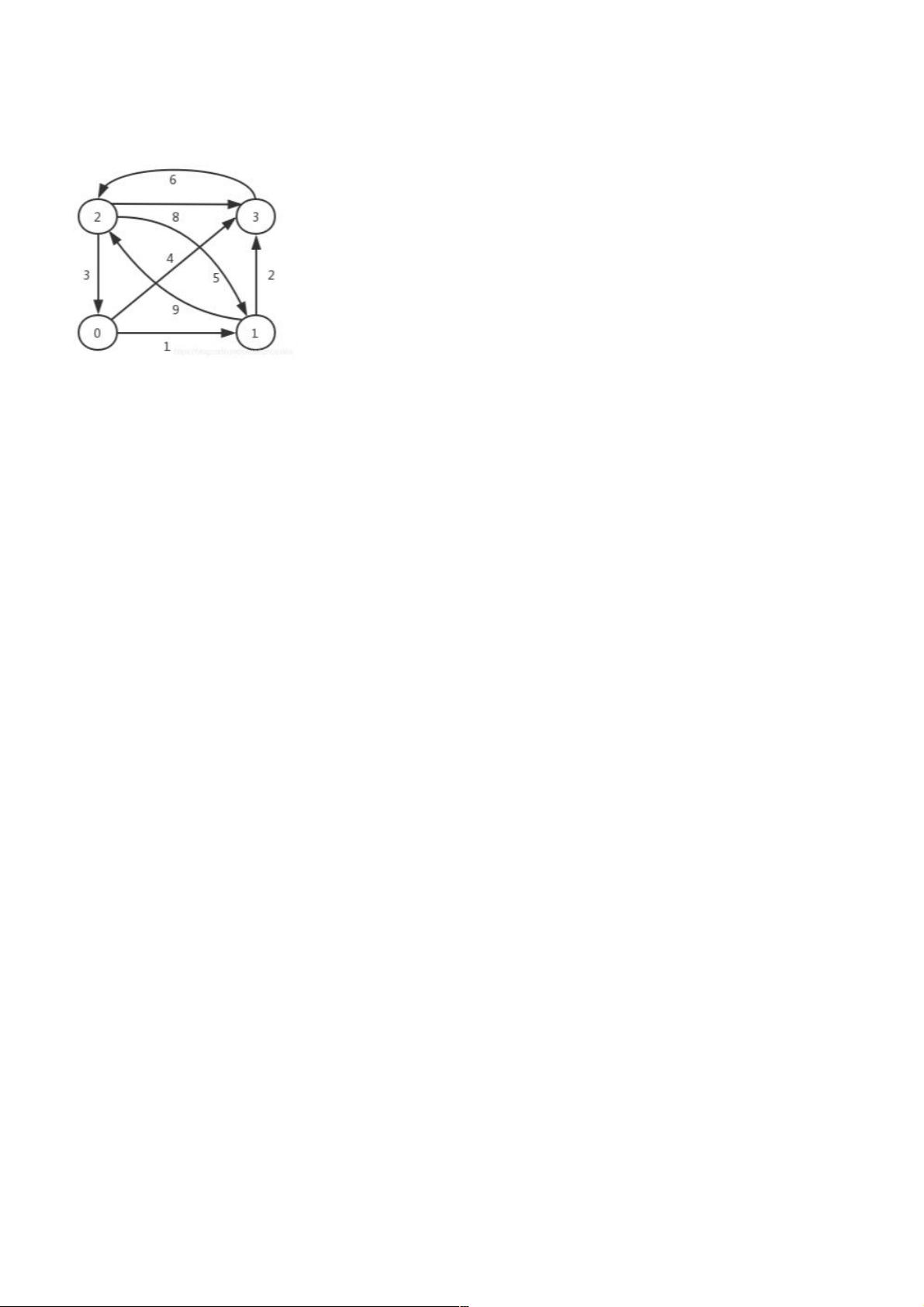 - 实例中的演示： - 当k=0时，顶点2发现通过顶点0到顶点1和3的距离分别为3+1和3+4，都比原来路径短，于是更新dist[2][1]和dist[2][3]。 - 当k=1时，顶点2发现通过顶点1到顶点3的路径更短，于是再次更新dist[2][3]和path[2][3]。 4. **代码实现**： - 提供了一个C++类Graphlnk，它包含邻接表表示的图结构，以及inputGraph()和outputGraph()方法用于输入和输出图的信息。 - 代码中还定义了Edge和Vertex结构体，分别表示边和顶点，包括它们的属性如目的地、成本和连接关系。 总结来说，本文通过实例展示了如何在C++中使用Floyd算法处理有向图的最短路径问题，确保了没有负权边的前提下，有效地求解出所有顶点之间的最短路径。