C++ Floyd算法实现所有顶点间最短路径详解

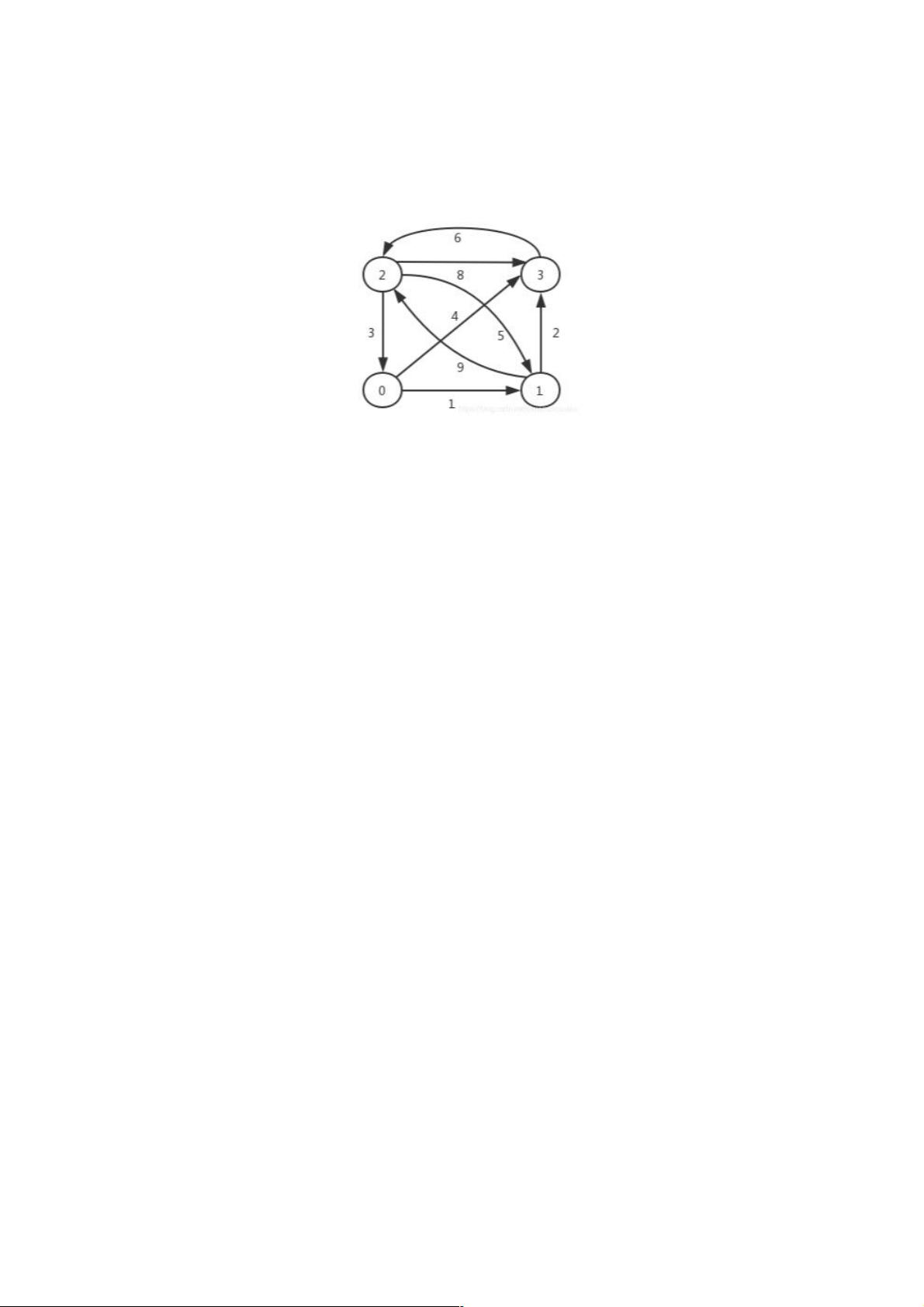
C++所有顶点之间的最短路径是一个在计算机图形学和算法设计中常见的问题，特别是在网络流分析或图论中。在这个主题中，我们关注的是如何在给定的有向图中找到任意两个顶点之间的最短路径。使用Floyd-Warshall算法是解决这个问题的一种有效方法。 Floyd算法，也称为Floyd-Warshal算法或Floyd's Cycle-Finding Algorithm，是一种动态规划策略，适用于解决图中的所有对最短路径问题。它的核心思想是通过迭代地考虑每一对顶点之间的中间顶点来更新最短路径。算法的主要步骤如下： 1. 假设不存在负权值的边，因为负权值可能导致路径无限循环。这个前提在实际应用中通常需要确保，或者在处理负权值时采取其他策略，如Dijkstra算法或Bellman-Ford算法。 2. 对于每个顶点i，依次将k设置为0到n-1（n为顶点总数），检查是否存在通过顶点k能够缩短i到其他顶点j的距离。具体来说，如果dist[i][k] + dist[k][j] < dist[i][j]，那么更新dist[i][j]为新的路径长度，并相应地更新path[i][j]以记录经过的路径。 3. 重复此过程直到k遍历完整个顶点集，每次迭代都会确保当前图中所有顶点对之间的最短路径是最优的。当k等于顶点总数减一（即n-1）时，算法完成，得到的结果dist[i][j]表示顶点i到顶点j的最短路径长度，而path[i][j]则是从i到j的路径序列。 在C++实现中，首先定义了有向图的结构体Edge和Vertex，分别表示边和顶点。接着，在Graph类中，有构造函数和析构函数，以及一个用于存储最大值的变量EmaxValue。Graphlnk类的实现则包含了这些基本结构，并实现了Floyd算法的逻辑。在代码中，用户可以通过创建Graphlnk对象并调用相应的成员函数来计算和存储所有顶点之间的最短路径。 学习和掌握C++中顶点间最短路径的求解方法不仅有助于理解图论的基本概念，还能提升编程技能，特别是在处理大规模数据和复杂网络结构时。通过Floyd算法，我们可以有效地找出图中任意两点之间的最优路径，这对于许多实际应用，如路由算法、网络分析和游戏AI等都有重要意义。