卷积码的维特比译码原理与应用

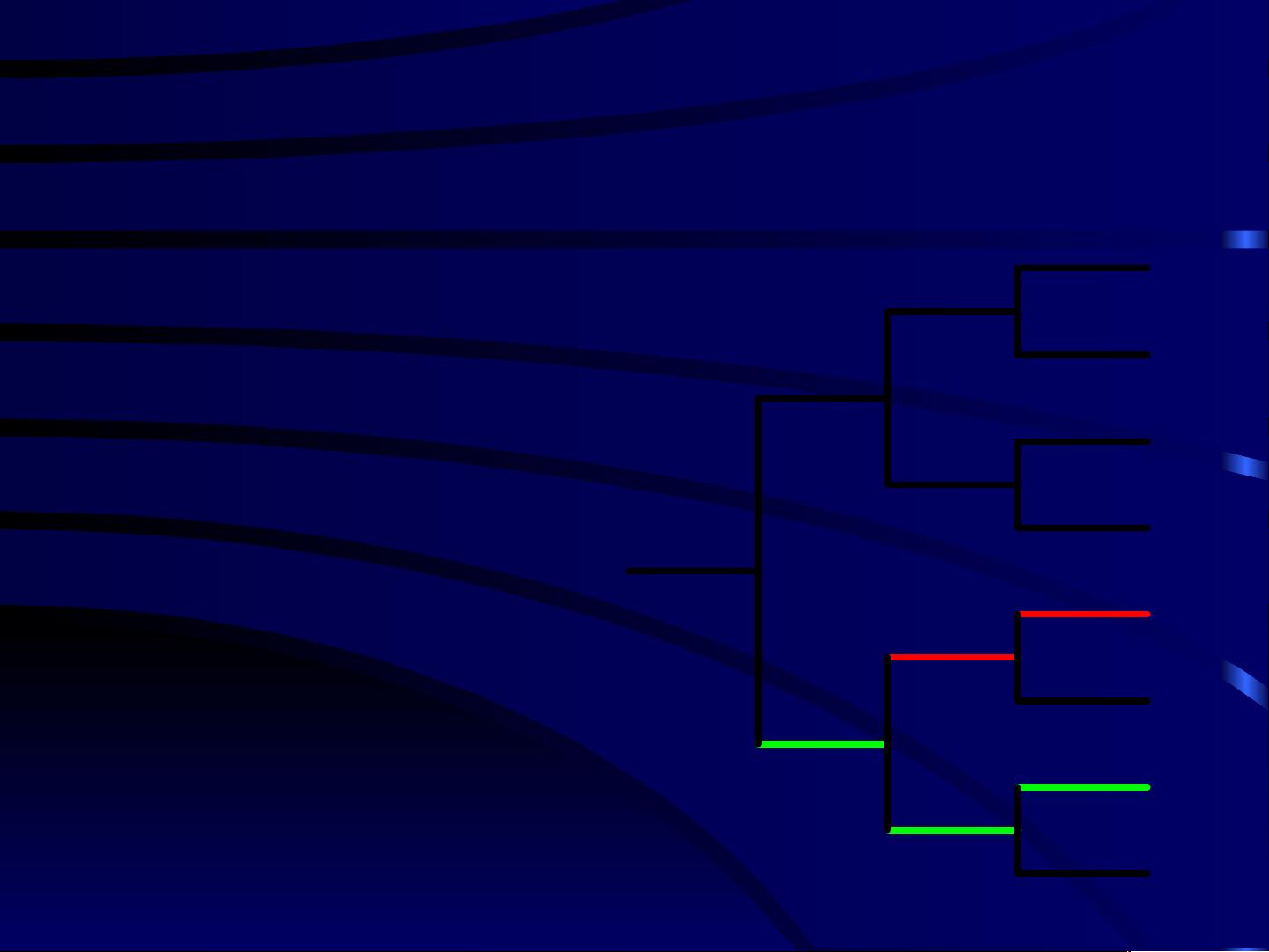
"本资源详细介绍了维特比译码及其在卷积编码中的应用，讨论了卷积码的性质和不同描述方式，并通过实例解析了逐分支译码和最大似然序列译码的方法，同时也指出了逐分支译码的局限性，强调了对数似然度量在译码中的重要性。" 卷积码是一种广泛应用于通信和数据存储领域的编码技术，它通过对信息流进行编码，引入一定的冗余，以提高传输或存储数据的可靠性。卷积码的特性在于其“记忆”功能，即当前编码状态不仅取决于当前的信息位，还与之前的部分信息位有关。这种记忆可以是线性的，可以用FIR（有限 impulse response）或IIR（无限 impulse response）滤波器来建模，也可以通过矩阵、树图或网格图的形式来表示。 在卷积码的译码过程中，概率译码是一种结合信道符号统计特性的方法。逐分支译码是最简单的实现方式，它沿着码树图的各个分支前进，每次选择与接收信号最匹配的分支。然而，逐分支译码未充分利用卷积码的记忆性，可能导致局部最优而非全局最优的解。 为了克服这一局限，最大似然序列译码（最大后验概率译码）被提出。其中，对数似然度量（log-likelihood metric）是关键，它衡量了给定码字条件下观测到接收序列的概率。当沿着正确的路径在码树中移动时，对数似然度量会呈现线性增长，而错误路径上的度量虽然可能短暂上升，但总体趋势会下降。然而，由于卷积码的记忆有限，错误路径可能在某个点与正确路径重合，形成局部错误，导致误码。 为了设计有效的译码算法，需要确保算法能够识别并及时修正错误路径。维特比译码算法就是这样一个解决方案，它基于动态规划原理，寻找码树中最优路径，从而最大化整个序列的似然度。维特比算法通过计算前向和后向指标，确保在任何时刻都选择了具有最高累积对数似然度的路径。 维特比译码是卷积码高效解码的关键，它利用对数似然度量在码树中找到最有可能的码字序列，从而显著提高了通信系统的误码率性能。理解并熟练运用维特比译码对于通信工程和信息处理领域的专业人士至关重要。