Mathematica与傅立叶变换详解

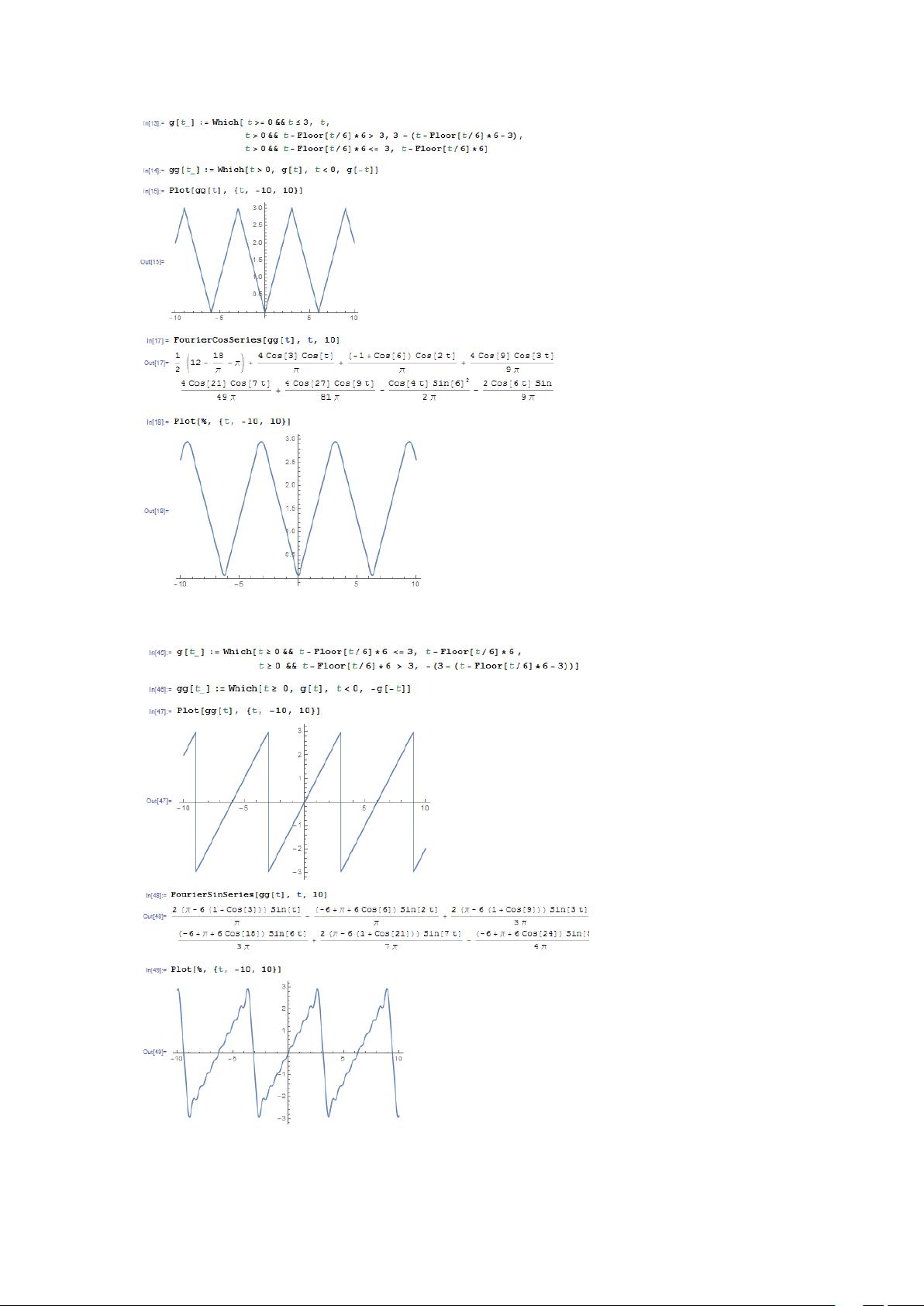
"这篇文档主要介绍了数学软件Mathematica在傅立叶变换方面的应用，包括傅立叶级数、傅立叶变换、离散傅立叶级数和离散傅立叶变换的基本概念以及相关函数的使用。" 在数学中，傅立叶分析是一种将信号分解成简单正弦和余弦波的方法，它在信号处理、图像分析、物理问题等领域有广泛的应用。Mathematica作为一个强大的数学计算工具，提供了丰富的函数支持傅立叶变换的操作。 1. **傅立叶级数**：傅立叶级数用于表示周期性信号，通过将信号分解为一系列不同频率的正弦和余弦项的和。Mathematica提供了`FourierCosSeries`和`FourierSinSeries`函数来分别对偶函数和奇函数进行傅立叶级数展开。例如，函数`e^(-t/2)`可以通过这两个函数进行傅立叶级数展开。 2. **傅立叶变换**：当信号是非周期的，可以使用傅立叶变换将其转换到频域进行分析。在Mathematica中，`FourierTransform`函数可以实现这一转换。傅立叶变换是傅立叶级数在周期趋向无穷大时的极限情况，将信号表示为所有频率的连续积分。 3. **离散傅立叶级数**：对于周期性的离散序列，如数字音频或图像，可以使用离散傅立叶级数（DFT）。Mathematica中的离散傅立叶级数与周期N相关的，可以通过N个独立的谐波叠加得到。 4. **离散傅立叶变换**（DFT）：对于非周期的离散序列，离散傅立叶变换提供了一种有效的分析方法。在Mathematica中，可以使用`Fourier`函数来计算DFT，而`InverseFourier`则用于进行逆变换，将频域表示恢复为时域序列。 在使用Mathematica进行傅立叶分析时，需要注意`FourierParameters`选项的设置，这会影响傅立叶级数和变换的公式，特别是积分范围和基频的定义。例如，在计算周期函数`t^2`的傅立叶级数时，通过调整`FourierParameters`可以正确地处理积分范围。 5. **傅立叶变换的复变性质**：傅立叶变换的结果`X[w]`可能是复数，其模长和幅角提供了关于信号频率成分的信息。Mathematica的`FourierTransform`函数可能使用不同的公式，但可以通过`FourierParameters`进行调整以匹配标准定义。同样，在进行傅立叶逆变换时，需要明确`t`为实数，可以通过`Assumptions`选项指定。 6. **离散傅立叶变换相关函数**：`Fourier`和`InverseFourier`是Mathematica中进行DFT和IDFT的主要函数。它们对离散序列进行快速高效的傅立叶变换，这对于处理大量数据非常有用。 Mathematica提供了强大而灵活的工具来执行傅立叶分析，无论是周期信号的傅立叶级数，还是非周期信号的傅立叶变换，甚至是离散序列的DFT和IDFT，都能得到准确且直观的结果。理解和熟练使用这些函数，对于进行傅立叶分析和信号处理工作至关重要。