提高效率的三角函数逼近算法：查表与泰勒级数

三角函数逼近快速算法(正余弦)是一个关注如何提高计算机程序中正弦(sine)和余弦(cosine)函数计算效率的方法。在实际编程中，如Java开发中，标准库提供的数学函数如`Math.sin()`和`Math.cos()`可能在精度需求较高的场景下显得效率低下，尤其是在处理高频波动或精确模拟时。本文档来源于两个在线资源：http://lab.polygonal.de/2007/07/18/fast-and-accurate-sinecosine-approximation/ 和 http://www.devmaster.net/forums/showthread.php?t=5784。 文章介绍了一种通过查表结合插值的方式来优化三角函数计算。这种方法利用预先计算好的一组精确值存储在一个表中，当需要计算时，根据输入的x值找到对应的近似值，然后通过插值技术进行进一步的调整，以达到更高的效率。这种方法的优点在于能够快速得到一个近似的值，而不需要像泰勒级数那样进行多次高精度计算。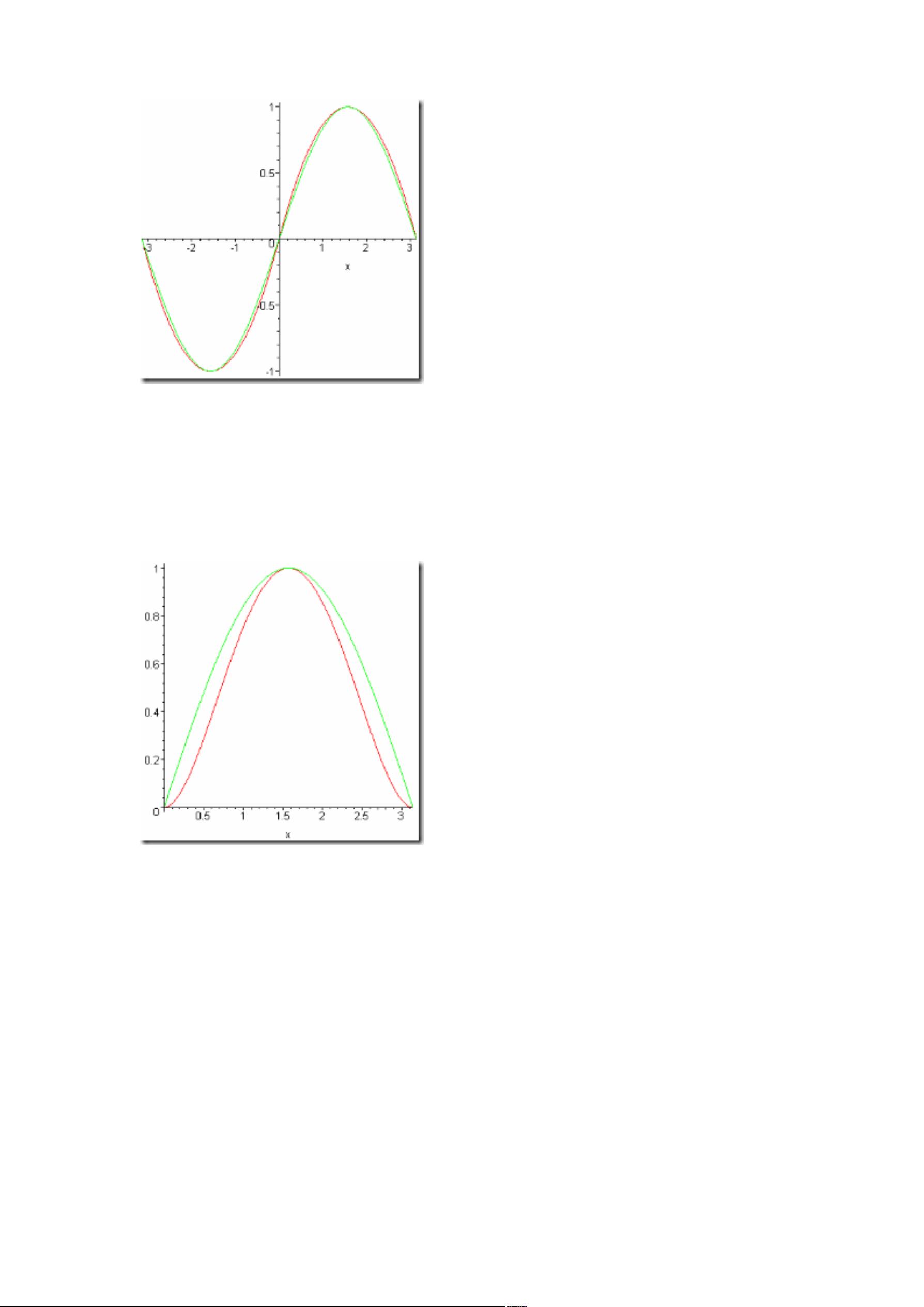 泰勒级数是另一种常用的方法，它基于函数的无限项展开，例如sin(x)的泰勒级数为x - x^3/6 + x^5/120 - x^7/5040 + ...。虽然泰勒级数理论上能提供极高的精度，但随着项数的增加，所需的计算量也随之增大，不利于效率提升。文档中提到的4项泰勒级数展开式已经足够在大部分应用场景中提供较好的近似，但其在π/2之后的精度下降和对π的误差问题暴露了这一方法的局限性。 此外，作者观察到4项泰勒级数的结果呈现出类似抛物线的形状，因此提出了寻找一个更符合正弦函数特性的抛物线公式A + Bx + Cx^2作为替代方案。通过设置三个条件，即抛物线在x=0、π/2和π处的函数值，可以求解出抛物线的系数，从而构造一个既能满足精度又能提高效率的近似公式。 这篇文档提供了三角函数逼近的一种创新思路，通过结合查表插值和抛物线拟合，为开发者在特定情况下提供了优化三角函数计算的实用技巧，尤其是在追求速度和较低精度需求的场景中。然而，实际应用时需要根据具体项目的需求和性能要求，选择最合适的逼近方法。