深入理解：分枝限界法原理与单源最短路径应用

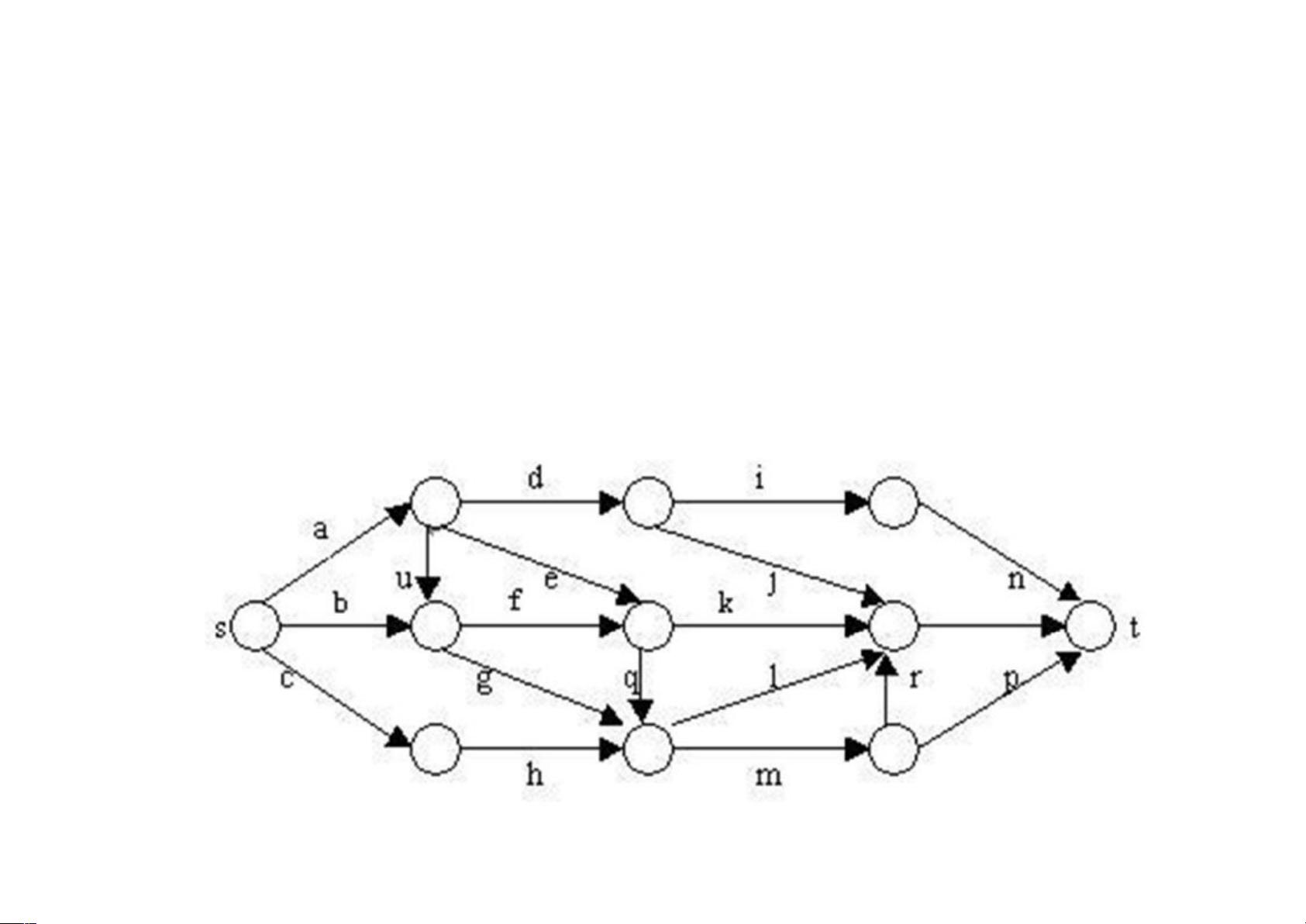
第二十一讲的主题是“分枝定界法”，这是一种在算法分析与设计中常用的搜索策略，用于在解决复杂问题时高效地探索解空间。本讲主要分为以下几个部分： 1. 基本思想：分枝限界法的核心是广度优先或最小耗费优先（如最大效益优先）地搜索问题的解空间。每个活结点在扩展过程中只允许被选择一次，非最优解或导致不可行的子结点会被放弃，其他符合条件的子结点则会加入活结点表。 2. 与回溯法的区别：与回溯法不同，分枝限界法的目的是找到满足约束条件的最优解，而非所有可能的解。回溯法则以深度优先搜索，而分枝限界法可以是广度优先或优先级搜索。 3. 常见的实现方法：包括队列式（FIFO）分枝限界法，按照结点添加的顺序决定扩展顺序；以及优先队列式分枝限界法，根据特定问题的特性选择最大优先队列或最小优先队列，以提高效率。 4. 以单源最短路径问题为例：通过一个具体的有向图G，展示了如何应用优先队列式分枝限界法寻找从源顶点s到目标顶点t的最短路径。解空间树中的每个结点都有一个对应当前路径长度的标签。 5. 算法实现：对于单源最短路径问题，算法采用极小堆来维护活结点表，优先级由结点的当前路径长度决定。初始时，源顶点s和空堆开始，然后逐步扩展节点，检查相邻顶点，更新路径长度。 总结来说，分枝限界法是一种灵活的搜索策略，通过合理的分支决策和剪枝策略，有效地在解空间中搜索，特别适用于那些需要找到最优解的问题，如最短路径、旅行商问题等。理解和掌握这种方法对于设计高效的求解算法至关重要。