N < 4超对称形状因数研究：Tr(F3)与最大超越性

"这篇学术论文详细探讨了超对称形状因数在量子色动力学（QCD）中的应用，特别是在希格斯玻色子与胶子振幅计算中的作用。作者深入研究了由运算符Tr(F3)产生的有限顶级质量校正，从N $$ \mathcal{N} $$ = 4的超级杨-米尔斯理论扩展到N $$ \mathcal{N} $$ < 4的情况，针对三个胶子和最多两个能级的循环。文章指出，与最大超对称性理论中的受保护三线性算子相关的Catani余数的最大超越部分是通用的，并且与N $$ \mathcal{N} $$ = 4理论中的形状因子相等。此外，他们发现较低超对称性的项包含了一些意外的小项，如ζ2，ζ3和对数的简单幂，这些都得到了清晰的表达。" 在QCD中，形状因子是理解基本粒子相互作用的重要工具，特别是在涉及希格斯玻色子和胶子的振幅计算时。这篇论文聚焦于Tr(F3)运算符，这是一个与经典维度增长相关的算子，其形状因子对于理解希格斯玻色子与胶子的相互作用至关重要。作者使用有效的场论技术来研究这个运算符在不同超对称度N $$ \mathcal{N} $$ 下的行为。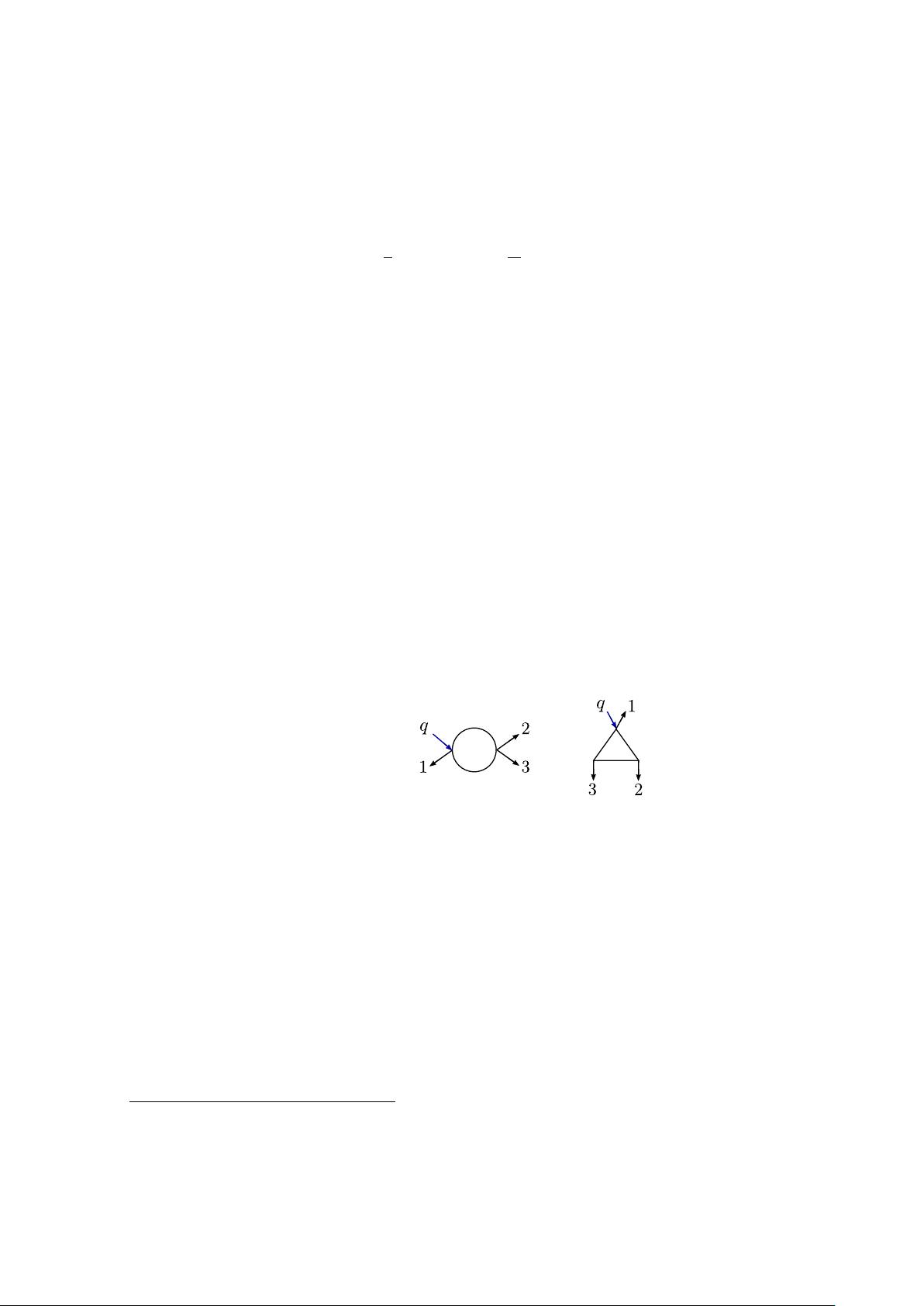 N $$ \mathcal{N} $$ = 4超级杨-米尔斯理论是一个高度对称的理论，其中的形状因子具有特殊的性质。在这个理论中，某些形状因子是受保护的，意味着它们在量子修正下保持不变。这篇论文扩展了这些结果，将分析范围扩大到N $$ \mathcal{N} $$ < 4的理论，揭示了在三个胶子振幅和两个能级的循环中，Tr(F3)形状因子的一致性和通用性。 论文的一个关键发现是，Catani余数函数的最大超越部分在各种超对称度下保持不变，这表明这个特性在不同理论中是通用的。这种超越性是量子场论中一个重要的数学属性，它与物理过程的复杂性有关。此外，对于那些具有更低超对称性的项，研究者观察到了与N $$ \mathcal{N} $$ = 4答案不完全匹配的小项，这些小项包括ζ函数（如ζ2和ζ3）以及对数的简单幂。这些发现提供了更深入的理解，有助于完善对QCD中复杂相互作用的描述。 该研究的成果对于理论物理学家和粒子物理学家来说具有重要意义，因为它加深了我们对超对称理论的理解，同时也为实验数据的解释提供了理论基础。此外，由于这项工作采用了开放获取的形式，使得全球的研究者都能访问并利用这些研究成果，促进了科学知识的共享和进步。