MATLAB实现洛伦兹方程混沌理论仿真

"本文将介绍如何使用MATLAB来模拟洛伦兹方程，这是一种用于描述非线性动力学系统的方程，与混沌理论密切相关。洛伦兹方程由美国气象学家爱德华·诺顿·洛伦兹提出，揭示了在特定参数下，简单系统可能产生复杂的非周期行为。" 洛伦兹方程是一组非线性常微分方程，其形式如下： \[ \frac{dx}{dt} = \sigma(y - x) \] \[ \frac{dy}{dt} = x(\rho - z) - y \] \[ \frac{dz}{dt} = xy - \beta z \] 这里，\[ \sigma \], \[ \rho \], 和 \[ \beta \] 是三个参数，分别代表对流参数、温度比率和辐射冷却速率。洛伦兹在研究大气热对流时发现了这个方程，并且在特定参数（例如：\(\sigma = 10\)，\(\rho = 28\)，\(\beta = 8/3\)）下，洛伦兹方程的解表现出混沌行为，即初始条件的微小差异会导致最终结果的巨大不同，这就是著名的“蝴蝶效应”。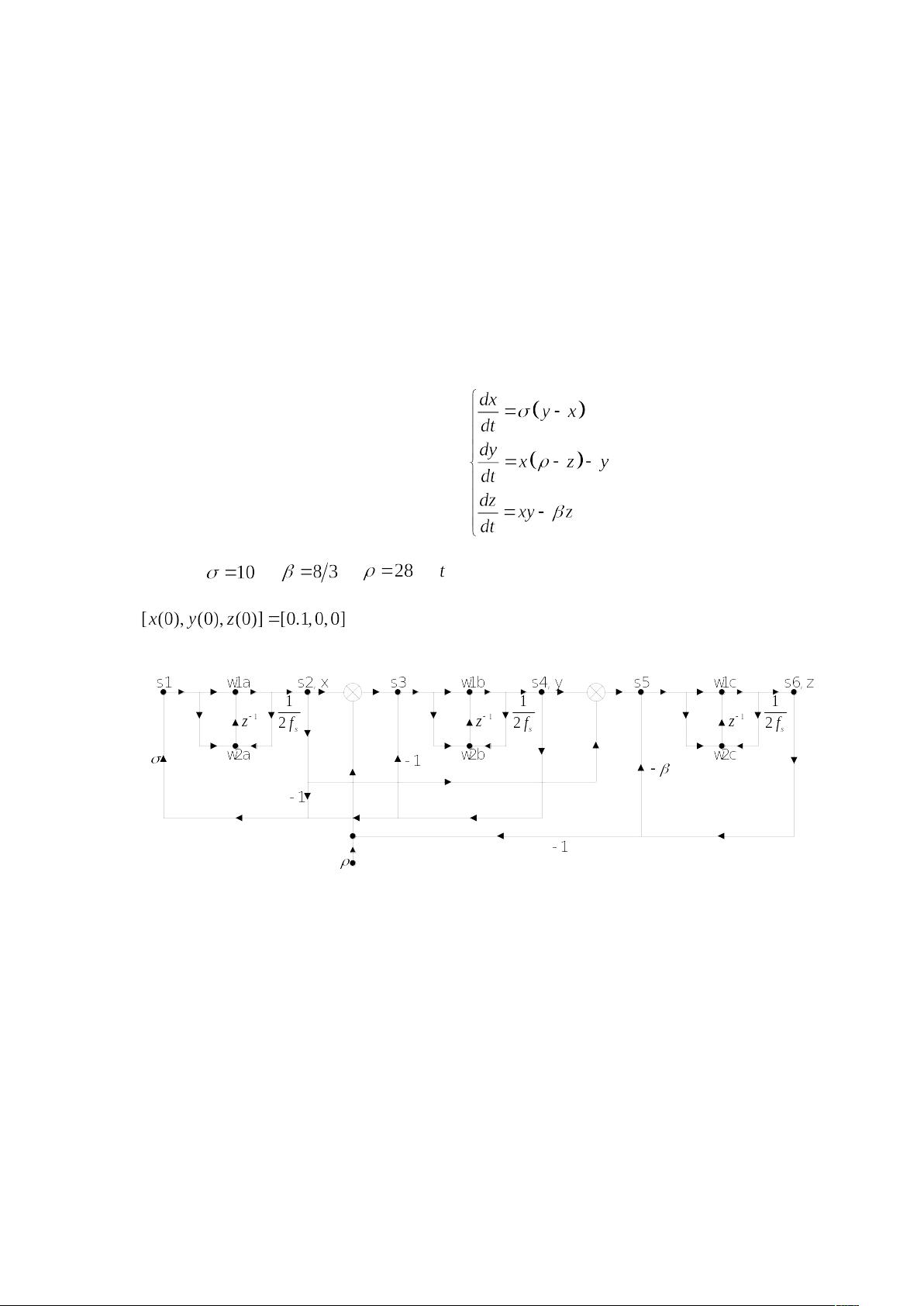 MATLAB是一种强大的数值计算工具，非常适合进行这种非线性动力学系统的仿真。在MATLAB中，可以使用ode45等数值积分器来求解这些微分方程。在信号流图中，粗黑点标记了仿真过程中的关键点。图3.22展示了求解洛伦兹方程的信号流图，而图3.23和图3.24则分别显示了两个不同的视角下的洛伦兹曲线仿真结果，呈现出混沌状态。 混沌理论在多个领域有着广泛的应用，比如气象学中的天气预报、物理学中的湍流现象、生物学中的种群动态，以及工程学中的控制系统设计等。19世纪60年代，Stephen Smale的工作进一步加深了我们对混沌现象的理解，他发现了一些物体在经历特定变换后会进入一种无序的混沌状态。 在MATLAB中仿真洛伦兹方程，通常涉及以下步骤： 1. 定义洛伦兹方程的函数。 2. 设置初始条件和参数。 3. 使用ode45或其他数值求解器进行积分。 4. 可视化结果，如绘制三维轨迹或二维投影。 以下是一个简单的MATLAB代码示例，用于模拟洛伦兹方程： ```matlab function dzdt = lorenz(t,z,sigma,rho,beta) dzdt = zeros(3,1); dzdt(1) = sigma*(z(2) - z(1)); dzdt(2) = z(1)*(rho - z(3)) - z(2); dzdt(3) = z(1)*z(2) - beta*z(3); end % 参数设置 sigma = 10; rho = 28; beta = 8/3; % 初始条件 z0 = [1;1;1]; % 时间范围 tspan = [0 50]; % 求解 [t,z] = ode45(@(t,z) lorenz(t,z,sigma,rho,beta), tspan, z0); % 可视化 figure; plot3(z(:,1), z(:,2), z(:,3)); xlabel('X'); ylabel('Y'); zlabel('Z'); title('洛伦兹方程仿真'); ``` 通过调整参数和初始条件，可以观察到洛伦兹方程产生的各种复杂行为，这进一步验证了混沌理论的核心观点：小变化可能导致大影响。