宽频线性调频连续波信号的多目标波达方向估计
需积分: 10 186 浏览量
更新于2024-09-07
收藏 1.78MB PDF 举报
"该资源是一篇发表在IEEE Transactions on Vehicular Technology期刊第67卷第8期（2018年8月）的文章，主要探讨了多目标环境中的线性调频连续波（LFMCW）信号的波达方向（AOA）估计方法。由Dongheng Zhang, Ying He, Xinyu Gong, Yang Hu, Yan Chen (IEEE高级会员) 和 Bing Zeng (IEEE会士) 合著。"
文章中介绍了一种新颖的线性调频连续波（LFMCW）信号的波达方向估计算法，特别是在多目标环境下的应用。LFMCW信号由于其出色的检测灵敏度和高距离分辨率，在目标检测与定位中被广泛应用。然而，当前对于多目标环境中每个目标反射LFMCW信号的AOA估计仍然存在局限。
该论文提出的方法利用一个发射天线和两个接收天线来发送宽频带LFMCW信号并接收来自不同目标的反射信号。信号处理分为三个步骤：
1. **解调**：首先，通过与发射信号混频，将接收到的宽带非平稳信号转换为一系列单音信号的叠加。这种操作有助于将复杂的宽带信号转化为可分析的形式。
2. **信号处理**：然后，对每个接收天线接收到的信号进行进一步处理。可能涉及到滤波、分帧、傅里叶变换等步骤，以便提取信号的特征。
3. **AOA估计**：最后，通过对处理后的信号进行分析，例如采用空间谱估计或阵列处理技术，来估计每个目标的到达角度。这可能包括使用双通道的相位差信息来确定信号到达的方向。
该方法可能涉及到的角度估计算法包括基于最小二乘法的解决方案，或者是基于迭代优化的算法，如期望最大化（EM）算法或基于机器学习的方法。此外，文中可能还讨论了算法的性能分析，包括误差性能、计算复杂度以及在有噪声和干扰情况下的稳健性。
这篇论文为多目标场景下的LFMCW信号AOA估计提供了新的思路，这对于雷达系统、无线通信和传感器网络等领域具有重要的理论和实践意义。通过优化信号处理流程，可以提高角度估计的精度和系统的整体性能。
ZHANG et al.: MULTITARGET AOA ESTIMATION USING WIDEBAND LFMCW SIGNAL AND TWO RECEIVER ANTENNAS 7103
where A
T
, f
min
, k, T
sweep
denote the amplitude of the signal,
the starting frequency of frequency modulation, the frequency
modulated slope, and the time duration of signal, respectively.
The instantaneous frequency of the LFMCW signal is
f =
1
2π
d(2πf
min
t + πkt
2
)
dt
= f
min
+ kt. (2)
In our system, the transmitted signal will be received by the
receiver after propagation. Suppose that the signal received by
the receiver antennas is reflected by a specific reflector. Then,
the received signal can be expressed as
r
0
(t)=A
R
e
j(2πf
min
(t−τ )+πk(t−τ )
2
)
, (3)
where A
R
and τ denote the reflected signal amplitude and the
time of flight (TOF), respectively. Comparing (1) and (3), we
can see that the received signal is a scaled and delayed version
of the transmitted signal.
According to [23], the amplitude A
R
can be expressed as
A
R
= A
T
R
√
G
T
G
R
d(t)
α
, (4)
where R denotes the reflection coefficient which is determined
by the radar cross section (RCS) of the reflector, G
T
and G
R
de-
note the gain of transmitter and receiver antennas, respectively,
d(t) denotes the propagation distance from the transmitter to the
reflector and back to the receiver, α is the attenuation coefficient
which is determined by the environment of propagation.
The time of flight τ is given by
τ =
d(t)
c
, (5)
where c is the velocity of light in the space.
As shown in Fig. 1, the received signal is the superposition
of a series of signals from different reflectors perturbed by the
noise of the receiver. Under the assumption that signals scatter-
ing and reflecting from unsmooth surface of the same reflector
are merged together because of the limited bandwidth, the ag-
gregated signal r(t) can be written as
r(t)=
N
i=1
A
Ri
e
j(2πf
min
(t−τ
i
)+πk(t−τ
i
)
2
)
+ w(t), (6)
where N is the number of reflectors, i denotes the index of
the ith path of propagation and w(t) is the zero-mean additive
complex white Gaussian noise at the receiver with variance σ
2
0
.
III. T
HE PROPOSED AOA ESTIMATION ALGORITHM
In this section, we describe the proposed AOA estimation
algorithm in detail. There are mainly three steps involved in the
proposed algorithm. First, the received signal is demodulated by
mixing with the transmitted signal to transform the wideband
non-stationary signal into superposition of a series of single-
tone signals. Second, the number of reflectors is determined
using hypothesis tests. Third, signals from different reflectors
are separated using bandpass filtering and the corresponding
AOA of each reflector is estimated using the phase difference
between two receiver antennas.
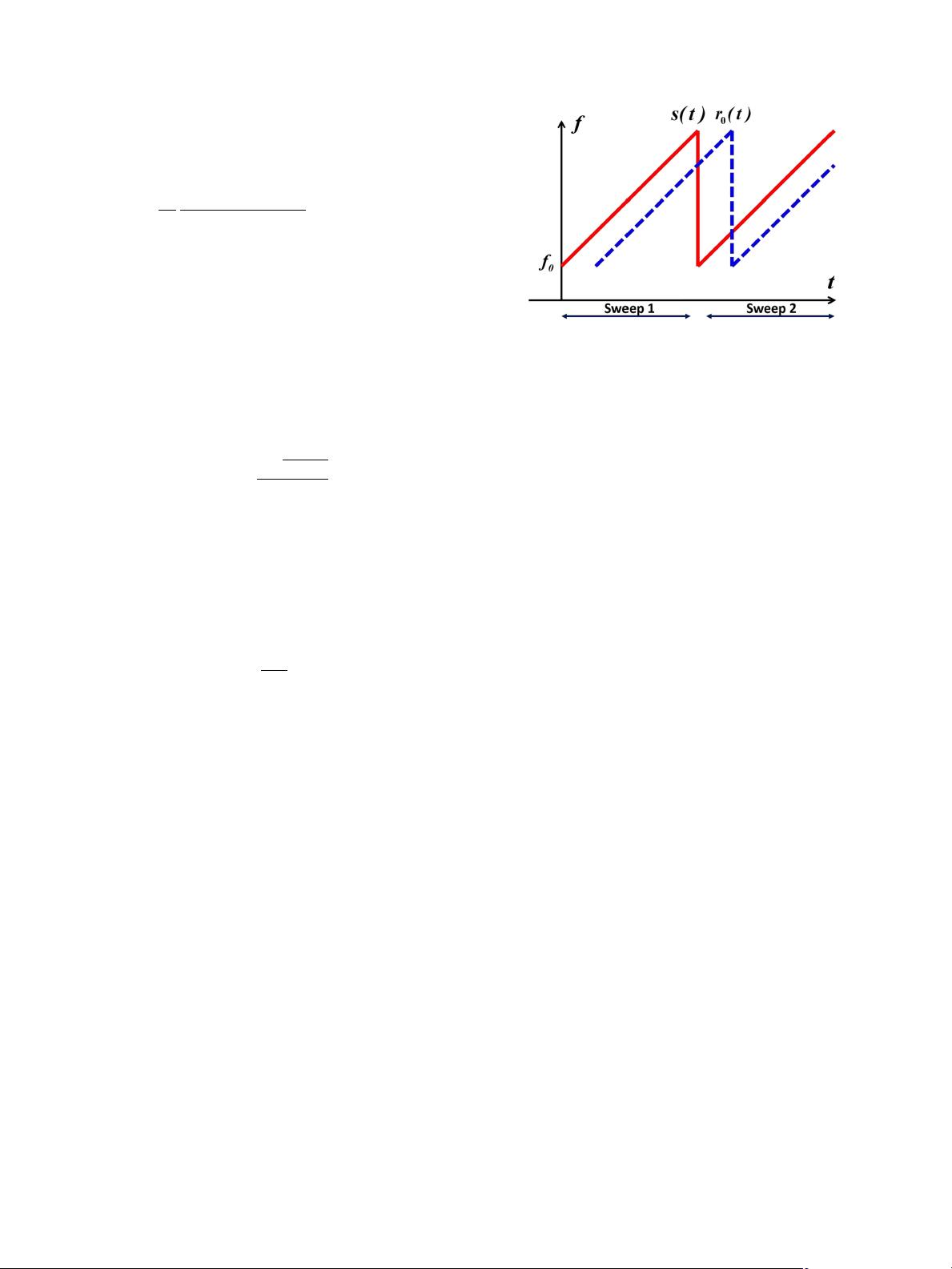
Fig. 2. An illustration of the transmitted signal and reflected signal.
A. Preprocessing of the Received Signal
LFMCW signal is a wideband non-stationary signal. Com-
pared to the transmitted signal, the received signal is attenuated
on amplitude and delayed in time. The frequency relation be-
tween the transmitted signal and received signal is shown in
Fig. 2. By utilizing the time delay characteristic of the received
signal, we can mix the received signal with the transmitted sig-
nal to extract the information about the reflector. Specifically,
the mixed signal can be written as
s
d
(t)=s(t)r
∗
(t)=
N
i=1
A
T
A
Ri
e
j(2πf
min
τ
i
+2πktτ
i
−πkτ
2
i
)
+ A
T
e
j(2πf
min
t+πkt
2
)
w
∗
(t). (7)
The first part in (7) corresponds to the signal that is the super-
position of a series of single-tone signals from different reflec-
tors. In t his paper, we assume that the distances of reflectors are
different. The frequency of this signal corresponds to the TOF,
which is determined by the distance from the transmitter to a
reflector and back to the receiver. In other words, the signals re-
flected from a specific distance have the same frequency and the
signals reflected from different distances have different frequen-
cies [24][25]. Note that although the Doppler shift will affect
the frequency of the received signal, when the frequency slope
of the LFMCW signal is high, the effect of the Doppler shift is
negligible. In such a case, bandpass filter can be used to sepa-
rate the signals from reflectors at different distances. The second
part in (7) corresponds to the cross-term of signal and noise. The
mixing process transforms the wideband non-stationary signals
into stationary signals with a single frequency, due to which
we can use classic signal processing techniques such as DFT to
extract the information of the signal.
In practice, the received signal is sampled by an A/D converter
to obtain its discrete version as follows:
s
d
(mT
s
)=
N
i=1
A
T
A
Ri
e
j(2πf
min
τ
i
+2πkmT
s
τ
i
−πkτ
2
i
)
+ A
T
e
j(2πf
min
mT
s
+πk(mT
s
)
2
)
w
∗
(mT
s
), (8)
where T
s
denotes the sampling interval.
剩余11页未读，继续阅读
2021-09-30 上传
235 浏览量
235 浏览量
155 浏览量
230 浏览量
2021-03-06 上传
206 浏览量
2022-07-13 上传
点击了解资源详情
zhangdh24
- 粉丝: 0
- 资源: 1
我的内容管理
展开
最新资源
- pattern in java
- java环境变量配置
- EN_62106-2001.pdf
- aspsqlscript
- A Guide to MATLAB Object-Oriented Programming -By Andy H. Register
- PIC24FJ1280使用手册
- DVD 与外部MCU通讯协议
- JSP笔记（doc格式）
- DOS常用命令,chg专业收集
- ‘the c++ standard’ 的 draft
- 关于ALV的最详细的汇总，包含各种功能
- excel转gis格式
- Linux Web Hosting with WebSphere，DB2，and Demino
- 基于vhdl的洗衣机控制器
- 基于vhdl的电子时钟设计
- Java面试经典100题（PDF）
