理解布隆过滤器：工作原理与实例分析

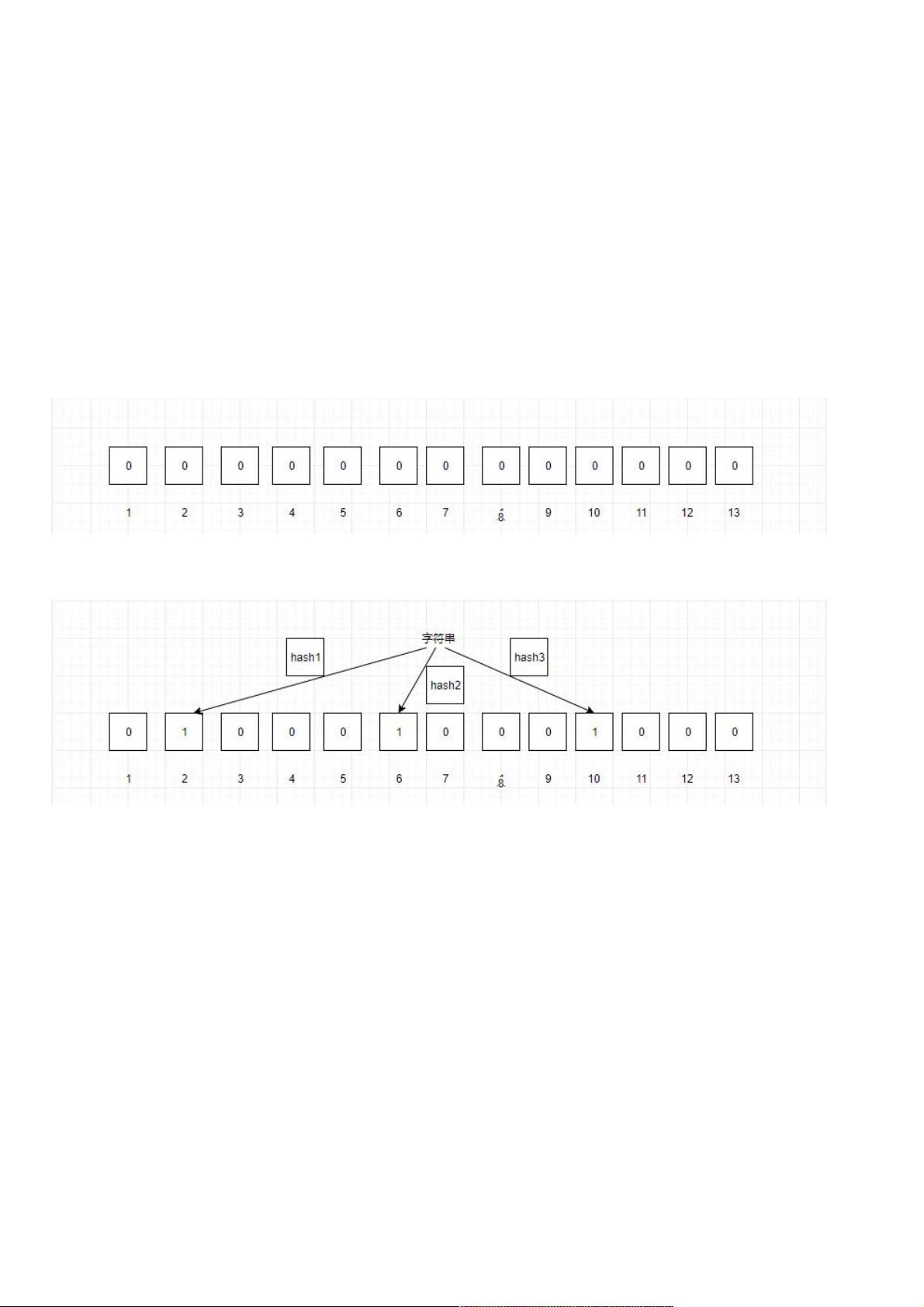
"本文主要介绍了布隆过滤器的工作原理及其应用实例，强调了其高效性和空间节省，同时指出其返回结果的概率性质可能导致误判。文章通过一个具体的例子展示了布隆过滤器如何运作，并讨论了如何选择合适的参数以降低误判率。" 布隆过滤器是一种在大数据处理和缓存系统中广泛应用的概率型数据结构，它主要用于判断一个元素是否可能存在于一个大规模集合中。由于其占用空间小、插入和查询速度快，特别适用于内存有限或需要快速响应的场景。然而，布隆过滤器的主要缺点是存在一定的误判率，可能会将不存在的元素误判为存在。 布隆过滤器的核心在于一个固定长度的二进制数组和一组独立的哈希函数。初始时，数组中的所有位都是0。当需要添加一个元素时，会用这组哈希函数将元素映射到数组的不同位置，将这些位置设为1。不同的哈希函数保证了元素可以均匀地分布在整个数组中。查询一个元素是否存在时，同样用这组哈希函数计算出数组中的位置，如果所有对应位置都是1，那么可能该元素存在（但不绝对）。如果存在0，则肯定不存在该元素。 误判主要源于两个原因：一是哈希函数的碰撞，即不同的元素可能映射到同一位置；二是有限的数组空间，随着插入元素的增多，未被插入的0逐渐减少，导致误判率上升。为了优化误判率，我们需要合理选择二进制数组的大小（m）和哈希函数的数量（k）。通常，m的选择与需要存储的元素数量（n）和期望的误判率（p）有关，可以通过理论公式进行计算。k的选择则影响着每个元素平均修改的位数，也影响误判率。 举例来说，如果需要存储100亿个元素，希望误判率为0.01%，那么根据理论公式计算，大约需要2000亿个bit的空间（约25GB）和14个哈希函数。实际应用中，我们还需要考虑计算这些哈希函数和操作数组的时间复杂度，以及如何设计这些哈希函数以尽可能减少冲突。 在编程实现布隆过滤器时，一般会使用一种称为开放寻址的策略来处理冲突，即当一个位置已被占用时，寻找下一个可用的位置。C语言或其他编程语言中，可以使用位操作来高效地设置和检查数组中的位。例如，C语言的实现可能包括定义一个大的unsigned long数组，利用位运算符（如<<和&）来实现哈希函数和位操作。 布隆过滤器是一种权衡空间和准确性的工具，适合于大数据环境下的快速查询。虽然其存在误判，但在许多应用场景中，这种微小的牺牲可以换取显著的性能提升。例如，在垃圾邮件过滤、URL去重、缓存系统等领域，布隆过滤器已经展现出强大的实用性。