支持向量机：原理、计算与决策边界详解

支持向量机（SVM）是一种强大的监督学习算法，主要用于分类和回归分析，特别适用于高维空间中的数据处理。它基于寻找最优的决策边界——支撑超平面，能够有效地处理线性和非线性可分问题。在处理线性不可分数据时，SVM引入了软间隔概念，通过最大化间隔（也称为“margin”），使得少数样本点可以位于正确类别的一侧，同时保持模型的泛化能力。 算法的核心思想是利用对偶问题和拉格朗日乘子法。原问题通常是一个凸优化问题，通过构建拉格朗日函数L(x,λ,v)，我们可以得到其对偶函数，这是一个关于λ和v的函数，对偶函数的凹性保证了优化的可行性。如果原问题存在最优解，那么对偶函数的全局最大值与原问题的最小值是相等的，这就是强对偶条件。KKT条件则是求解这些问题时的重要准则，它结合了原问题和对偶问题的最优解。 SVM的计算过程涉及寻找使间隔最大的支持向量，这些向量位于决策边界两侧，它们对于确定模型的稳健性至关重要。对于线性不可分的数据，核函数的使用使得算法可以扩展到非线性特征映射，通过将数据从原始空间映射到更高维度的特征空间，使得原本非线性的决策边界变得线性可分。 在实现上，SMO（Sequential Minimal Optimization，顺序最小优化）算法是一种有效的求解策略，它通过迭代地选择并优化两个训练样本来更新模型，直到达到全局最优解。这种方法在大规模数据集上也非常高效。 支撑超平面的概念是SVM的基础，它是集合C在点x0处的一个超平面，使得C中的所有点到该超平面的距离都大于等于某个常数，这确保了分类的稳定性。对于凸集，任何边界点都存在支撑超平面，反之亦然，这表明了凸集的几何特性。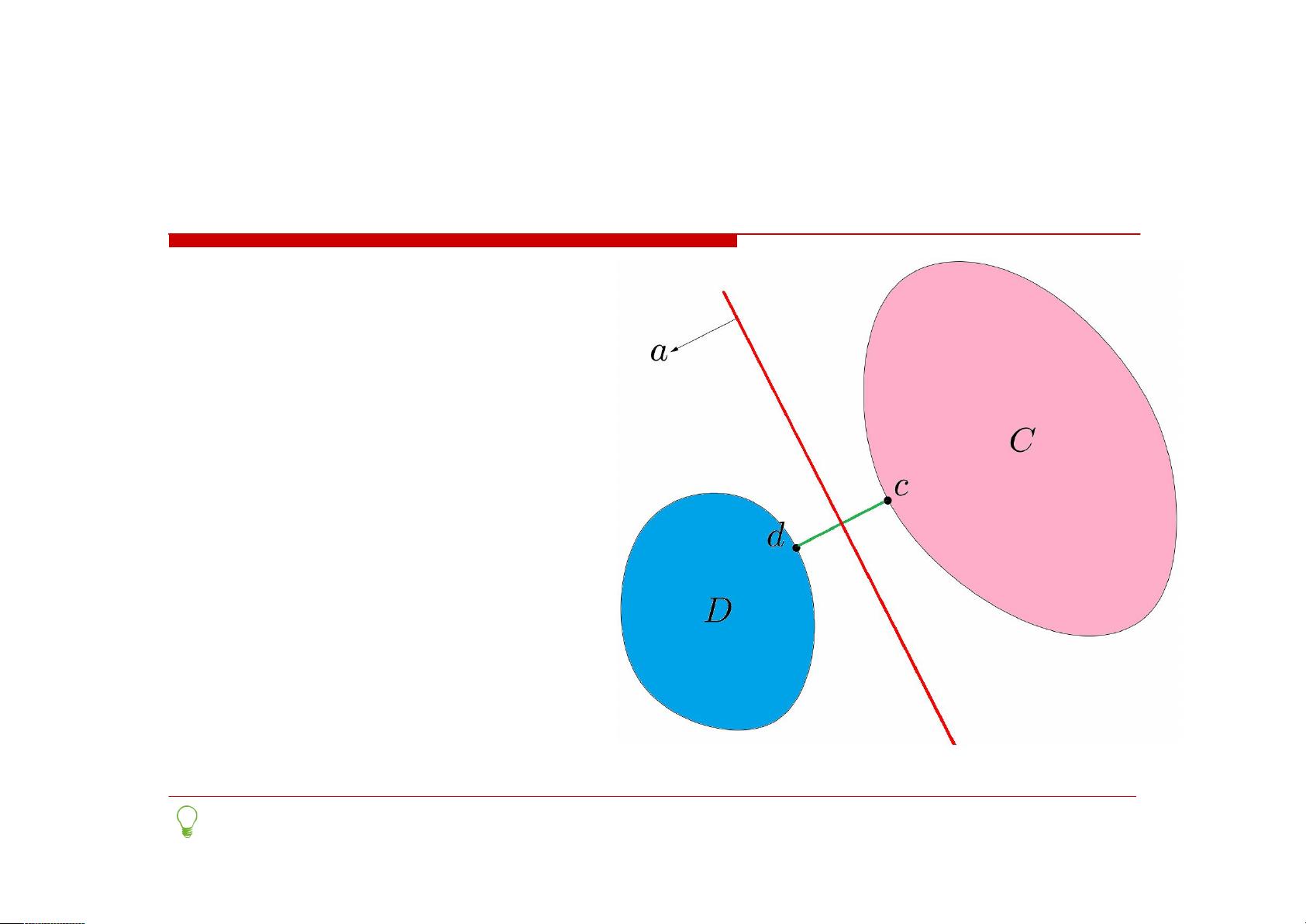 分割超平面则是用于将两个不相交的凸集C和D分开的超平面，它的关键在于找到两个集合之间的最大间隔。如果两个集合至少有一个是开集，那么存在分割超平面意味着它们不相交，这是判定它们是否可以被分离的重要条件。 最后，确定“最优”分割超平面涉及到计算两个集合间的距离，并通过构造最短距离的垂直平分线来实现。这个过程中，选择“边界”上的关键点作为参考，有助于找到最优的决策边界。 支持向量机通过巧妙的数学建模和优化技术，提供了一种既直观又强大的机器学习工具，尤其在处理复杂分类任务和高维数据时展现出其优势。