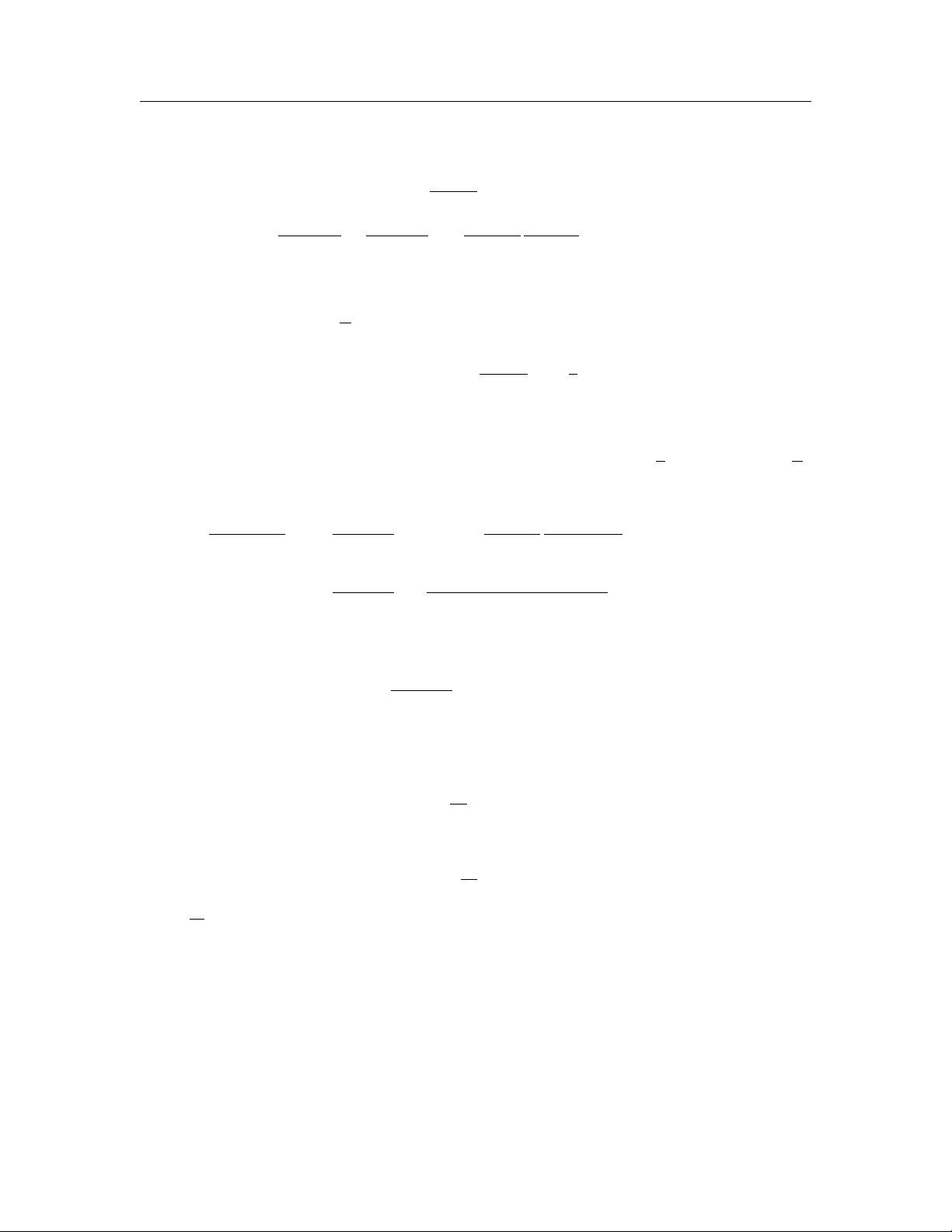时间分数阶慢扩散方程的纯显-隐交替并行计算新方法

"时间分数阶慢扩散方程的纯显-隐交替并行计算方法是由赵雅迪、吴立飞、孙淑珍和杨晓忠在华北电力大学数理学院研究提出的一种数值计算方法，用于处理时间分数阶慢扩散方程。此方法结合了古典显式格式、古典隐式格式与交替分段技术，形成具有并行特性的PASE-I（Pure Alternative Segment Explicit-Implicit）和PASI-E（Pure Alternative Segment Implicit-Explicit）差分格式。" 时间分数阶慢扩散方程在自然科学和工程领域有着广泛应用，特别是在描述反常扩散现象时，能够提供更精确的模型。该研究中的纯显-隐交替并行计算方法旨在解决这类方程的数值求解问题，同时提高计算效率。 PASE-I和PASI-E差分方法的创新之处在于它们将经典的显式和隐式格式交替使用，并通过交替分段技术实现并行计算。这种方法保证了解的存在唯一性，并通过傅里叶分析和数学归纳法证明了其无条件稳定性和收敛性。具体来说，格式在空间上具有二阶精度，在时间上则达到2-α阶收敛。 数值实验进一步证实了理论分析的准确性，显示PASE-I和PASI-E格式不仅在空间和时间上有较高的收敛率，而且在计算速度上显著优于传统的隐式格式，尤其体现出明显的并行计算优势。这使得该方法成为求解时间分数阶慢扩散方程的有效工具。 关键词涵盖的时间分数阶扩散方程、交替分段纯显隐格式、稳定性、并行计算以及数值试验，均体现了该研究的核心内容和技术特点。中图分类号O241.8将该工作归类为数学领域的数值计算方法研究。 这项研究为处理时间分数阶慢扩散方程提供了新的数值计算策略，该策略具有并行性和高效率，有望在实际问题的求解中发挥重要作用。