支持向量机(SVM)原理详解

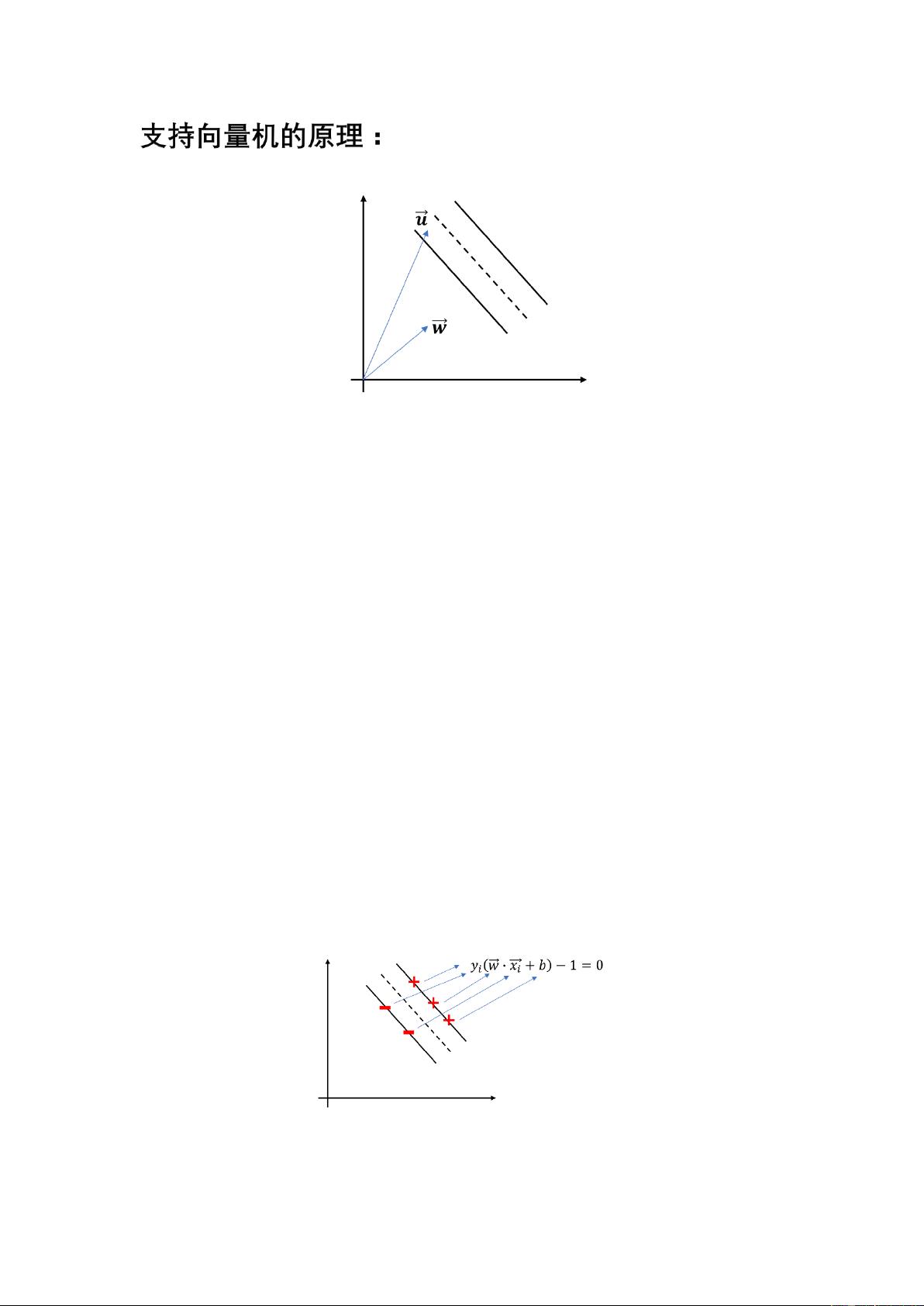
"这篇内容介绍了支持向量机（Support Vector Machine, SVM）的基本概念和优化目标。SVM是一种监督学习模型，主要用于分类和回归分析，它的核心思想是找到一个超平面，将不同类别的样本分开。这个超平面是使得两类样本距离最大化的边界，这个距离被称为间隔（Margin）。" 在SVM中，数据被表示为向量，超平面则是通过这些向量定义的决策边界。超平面由向量\( \mathbf{w} \)和常数\( b \)定义，其方程为\( \mathbf{w} \cdot \mathbf{x} + b = 0 \)。这里的\( \mathbf{x} \)是样本向量，\( \mathbf{w} \)是决定超平面方向的向量，\( b \)是偏置项，用于调整超平面的位置。 当向量\( \mathbf{u} \)与超平面的关系未知，但知道\( \mathbf{u} \cdot \mathbf{w} \geq c \)（其中\( c \)是常数，代表\( \mathbf{u} \)到超平面的距离），可以推断\( \mathbf{u} \)位于超平面的右侧。进一步，如果向量\( \mathbf{u} \)满足\( \mathbf{w} \cdot \mathbf{u} + b \geq 0 \)，则将其标记为正例，反之为负例。 然而，实际问题中，我们通常不知道最佳的\( \mathbf{w} \)和\( b \)。为了找到它们，需要引入更多的约束条件。对于正例\( \mathbf{x}_+ \)，要求\( \mathbf{w} \cdot \mathbf{x}_+ + b \geq 1 \)，对于负例\( \mathbf{x}_- \)，要求\( \mathbf{w} \cdot \mathbf{x}_- + b \leq -1 \)。同时引入变量\( y_i \)，正例取值为1，负例取值为-1。 约束条件可以表达为\( y_i(\mathbf{w} \cdot \mathbf{x}_i + b) - 1 \geq 0 \)，这意味着所有样本都必须满足这个不等式。当样本位于超平面边界上时，不等式取等号，即\( y_i(\mathbf{w} \cdot \mathbf{x}_i + b) - 1 = 0 \)。 SVM的目标是最大化间隔，也就是最小化\( \frac{1}{2} \|\mathbf{w}\|^2 \)。这样做的原因是，间隔等于\( 2/\|\mathbf{w}\| \)，因此最大化间隔相当于最小化\( \|\mathbf{w}\| \)，进而最小化\( \frac{1}{2} \|\mathbf{w}\|^2 \)。 为了解决这个问题，引入拉格朗日乘子法，构建拉格朗日函数： \[ \mathcal{L} = \frac{1}{2} \|\mathbf{w}\|^2 - \sum_{i} \alpha_i[y_i(\mathbf{w} \cdot \mathbf{x}_i + b) - 1] \] 其中，\( \alpha_i \)是非负的拉格朗日乘子，不能全为零。 通过对拉格朗日函数求导，得到如下条件： \[ \mathbf{w} = \sum_{i} \alpha_i y_i \mathbf{x}_i \] \[ \sum_{i} \alpha_i y_i = 0 \] 这表明，\( \mathbf{w} \)是由样本集中位于超平面边界上的样本\( \mathbf{x}_i \)加权和确定的，且\( \alpha_i \)是对应的权重。这些满足条件的样本称为支持向量，因为他们对超平面的定位至关重要。 总结起来，支持向量机的核心思想是找到一个能最大化类别间隔的超平面，通过优化拉格朗日函数来确定这个超平面的参数。这种方法不仅考虑了样本的分类，还考虑了样本到超平面的距离，从而保证模型具有良好的泛化能力。在实际应用中，SVM可以处理高维数据，并通过核函数技巧解决非线性分类问题。