分数延迟FIR梳状滤波器设计：线性相位与陷波特性

"基于分数延迟的有限冲激响应型梳状滤波器设计方法，用于处理非整数倍采样率与陷波频率关系的情况，结合高通滤波器和分数延迟滤波器，降低实现复杂度，适用于心电信号的基线漂移和工频干扰滤波。" 本文主要探讨了在信号处理领域，如何设计一种适用于非整数倍采样率与陷波频率关系的线性相位梳状滤波器。传统的梳状滤波器通常假设采样率与陷波频率是整数倍关系，但在实际应用中，这种假设并不总是成立。为了解决这一问题，作者提出了一种创新的设计方法，即结合高通纠漂滤波器和分数延迟滤波器。 首先，高通滤波器用于纠正基线漂移，这是一种常见的信号处理技术，特别是在生物医学信号如心电信号的分析中。基线漂移可能导致信号失真，影响后续的分析和诊断。而分数延迟滤波器则能够在非整数倍采样率下实现所需的频率选择性，这是通过引入精确的分数样本延迟来实现的，它可以更精确地定位陷波频率。 其次，采用多相滤波结构代替直接结构来实现基于分数延迟的FIR（有限冲激响应）型梳状滤波器，这种结构降低了实现的复杂度。多相滤波器通过将滤波器分解成多个低阶滤波器，使得计算和实现更为高效，这对于资源受限的系统特别有利。 在具体应用中，这种方法被应用于有基线漂移、工频及其谐波干扰的心电信号的滤波处理。心电图（ECG）信号容易受到环境电磁干扰，如工频（50Hz或60Hz）及其谐波的影响，这些干扰会淹没或扭曲真实的心电信号。通过所设计的梳状滤波器，这些干扰可以有效地被消除，从而提高心电图的分析精度和可靠性。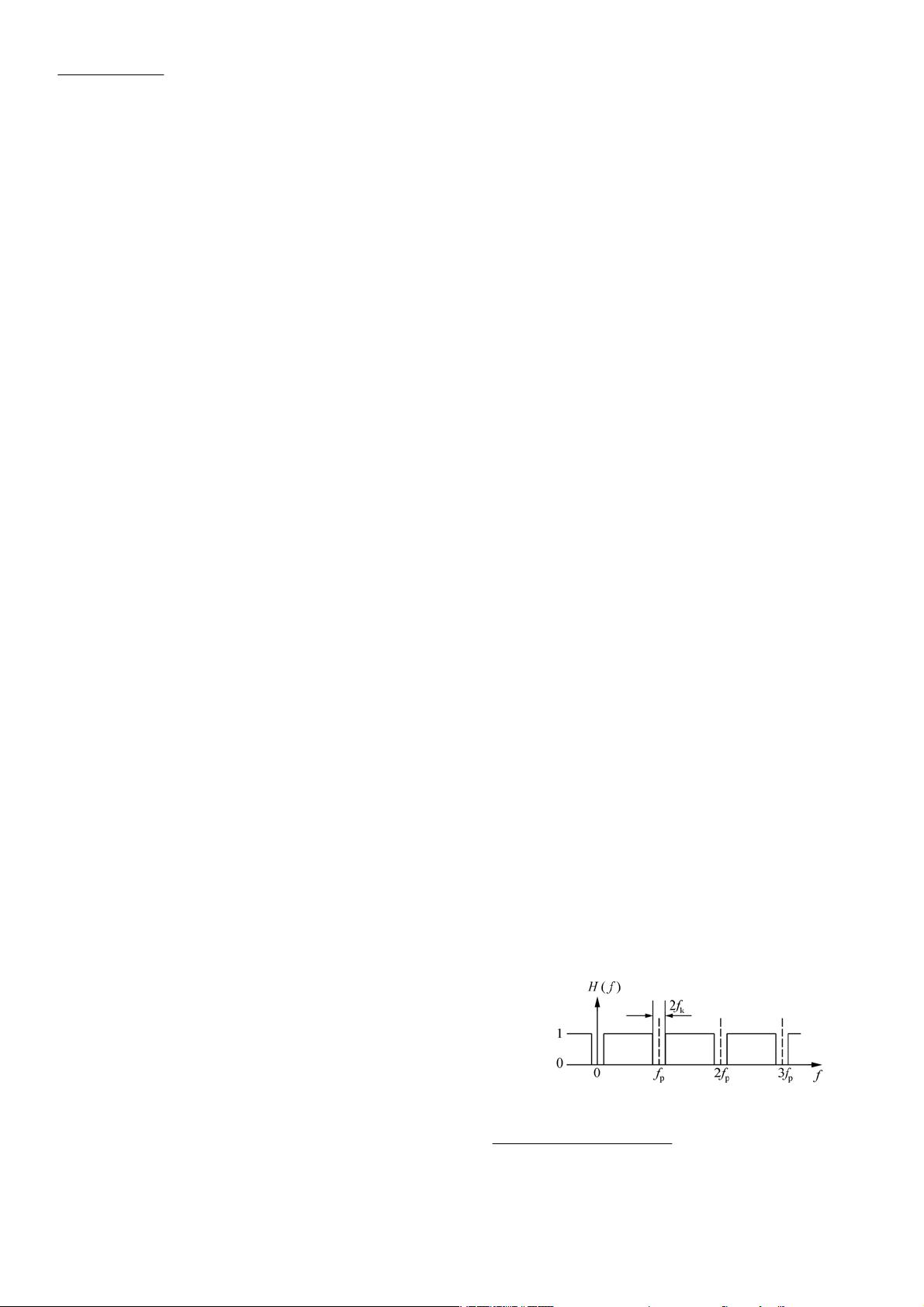 此外，该滤波器在通带内保持线性相位，这意味着在不需陷波的频率范围内，信号的相位变化是均匀的，这有助于保持信号的时域特性不变。而在陷波点上，滤波器基本保持了高通滤波器的陷波特性，能够有效地去除特定频率的干扰。 该研究提出了一种新的梳状滤波器设计策略，它在处理非整数倍采样率与陷波频率关系的信号时表现出优越的性能，特别是在心电信号处理中，对于基线漂移和工频干扰的滤除有显著效果。这一方法不仅理论上有意义，而且在实际应用中具有很高的价值，为生物医学信号处理提供了新的工具。