优化Spark容器部署：隔离、安全与性能

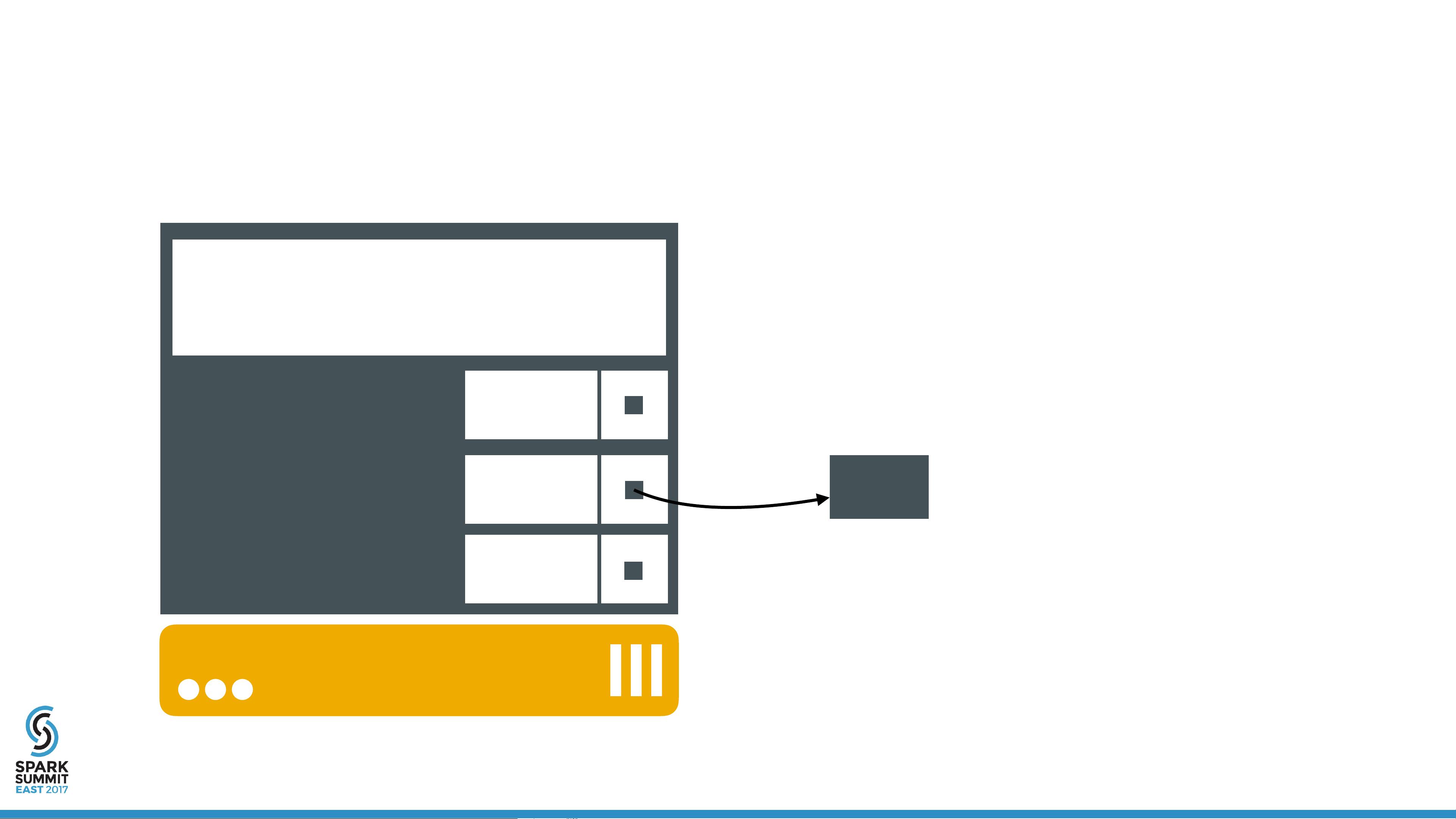
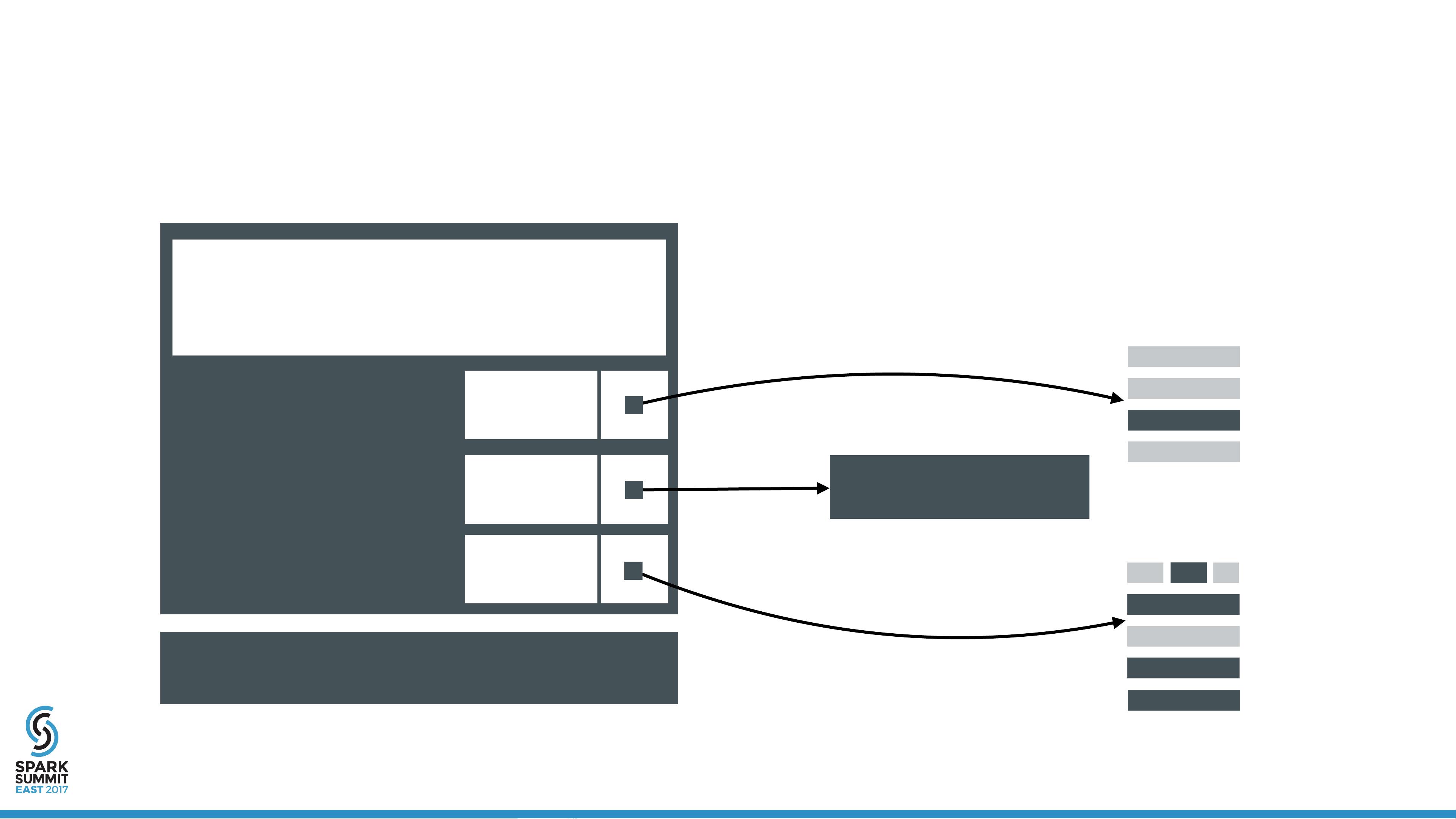
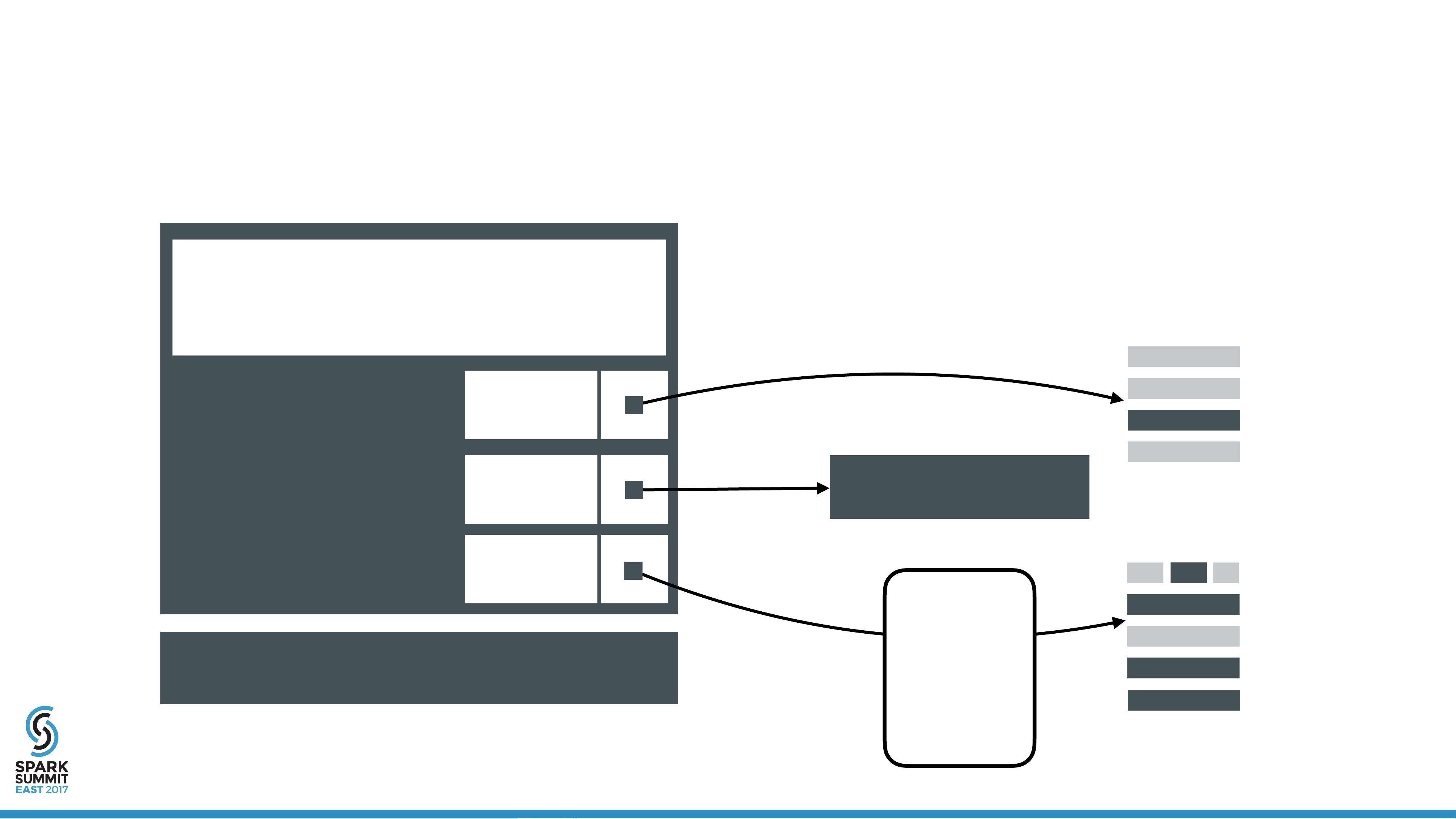
“藏经阁-OPTIMIZING SPARK DEPLOYMENTS FOR CONTAINERS_ ISOLATION, SAFETY, AND PERFORMANCE_ 阿里云” 本文档主要探讨了如何优化在容器环境中部署Apache Spark的工作，关注点在于隔离、安全性和性能。由Red Hat公司的William Benton撰写，他详细阐述了背景、架构问题、安全问题、性能问题以及结论和关键要点。 1. **背景与定义** 容器技术作为一种轻量级虚拟化方式，提供了一种将应用程序与其依赖环境打包的机制，确保在不同环境下的一致性。Spark是一种用于大规模数据处理的开源计算框架，它通常在分布式集群上运行。在容器环境中部署Spark，可以实现更好的资源隔离和更灵活的调度。 2. **架构问题** - **资源隔离**：容器提供了一种在不同应用之间隔离资源的方式，如CPU、内存和磁盘空间，这对于多租户环境中的Spark部署尤为重要，确保每个作业都能得到公平的资源分配。 - **调度优化**：在容器环境中，需要考虑如何有效地利用容器编排工具（如Kubernetes或Docker Swarm）来调度Spark任务，以提高集群效率。 - **网络配置**：由于Spark作业通常涉及节点间通信，容器内的网络配置需确保低延迟和高吞吐量。 3. **安全问题** - **容器安全性**：确保每个Spark容器的安全，防止恶意攻击或数据泄露，这可能涉及到容器镜像的签名验证、网络策略的设置以及访问控制的实施。 - **数据保护**：在容器中运行Spark作业时，要保护数据的机密性和完整性，可能需要加密存储和传输，以及严格的数据访问策略。 - **权限管理**：容器内的用户和进程权限需要精细管理，防止未经授权的访问和操作。 4. **性能问题** - **资源限制**：合理设定容器的CPU和内存限制，避免过度分配导致的性能下降。 - **I/O性能**：优化容器与宿主机之间的I/O交互，减少瓶颈，例如使用持久卷挂载或优化网络文件系统（NFS）性能。 - **Spark配置调整**：根据容器环境调整Spark的相关配置，如executor数量、大小以及并行度等，以适应容器化部署的特性。 5. **结论和关键要点** 文档最后总结了优化Spark在容器中部署的关键点，并提出了改进策略，可能包括最佳实践、监控和自动化工具的使用，以及持续的性能调优过程，以确保在保证安全和隔离的同时，达到理想的性能水平。 通过理解这些关键点，读者将能够更好地设计和实现一个高效且安全的Spark容器化部署方案，特别是在阿里云这样的云平台上，这些知识将有助于最大化利用云计算资源并降低运维复杂性。