e Scientic World Journal
Step 1. Generate an initial solution ;let
=and
∗
=.
Step 2. Generate a certain number of neighboring solutions
around the given solution
, nd the best neighboring
solution
, and update the best solution found so far.
Step 3. Let =Accept(
,).
Step 4. If the stop condition is not satised, generated
=
perturb(), go back to Step ; otherwise, stop the algorithm.
3.2. Particle Swarm Optimization. In , mimicking the y-
ing behavior of a swarm of birds, a novel optimization algo-
rithm named particle swarm optimization (PSO) was devel-
oped by Kennedy and Eberhart, which has been veried e-
cient for solving both continuous and discrete optimization
problems []. During recent years, many researchers have
applied PSO for solving lots of optimization problems [–
].
e owchart of the canonical PSO is given as follows.
Step 1. Set the system parameters, such as the initial popula-
tion size, the possibility (
𝑙
) for learning from local best, and
the possibility (
𝑔
) for learning from the best solution found
so far.
Step 2. Generate the initial population of particles.
Step 3. Store each particle into a vector named local best,
where each solution corresponds to the local best of the
corresponding particle. Memorize the best solution found so
far.
Step 4. For each particle, perform the following steps until
the stop condition is satised.
Step 5. Randomly generate a number
1
between and , if
1
is less than
𝑙
, and then perform the learning process from
the local best of the current particle.
Step 6. Randomly generate a number
1
between and , if
1
is less than
𝑔
, and then perform the learning process from
the global best of the current particle.
Step 7. Record the local best for each particle and the global
best found so far.
Step 8. Learn by itself.
Step 9. Go back to Step .
4. Framework of the Proposed Algorithm
4.1. Solution Representation. For solving the HFS scheduling
problems with PM activity, we use the permutation represen-
tation mechanism. Give a HFS scheduling problem jobs,
stages, and machines; each solution is represented by a
vector of integer values, where each integer value represents
a job number. erefore, the length of the solution equals the
number of jobs. For example, for a HFS problem with ten jobs
2 3 1 5 6 8 4 9 10 7
J
2
J
2
J
3
J
6
J
8
J
4
J
9
J
7
J
1
J
10
F : Solution representation.
Stage 2
Stage 1
Stage 3
PM
Aected operation
M
1
M
2
M
3
M
4
J
2
J
2
J
3
J
4
J
1
J
1
J
1
J
3
J
3
J
2
J
4
J
4
t
1
t
2
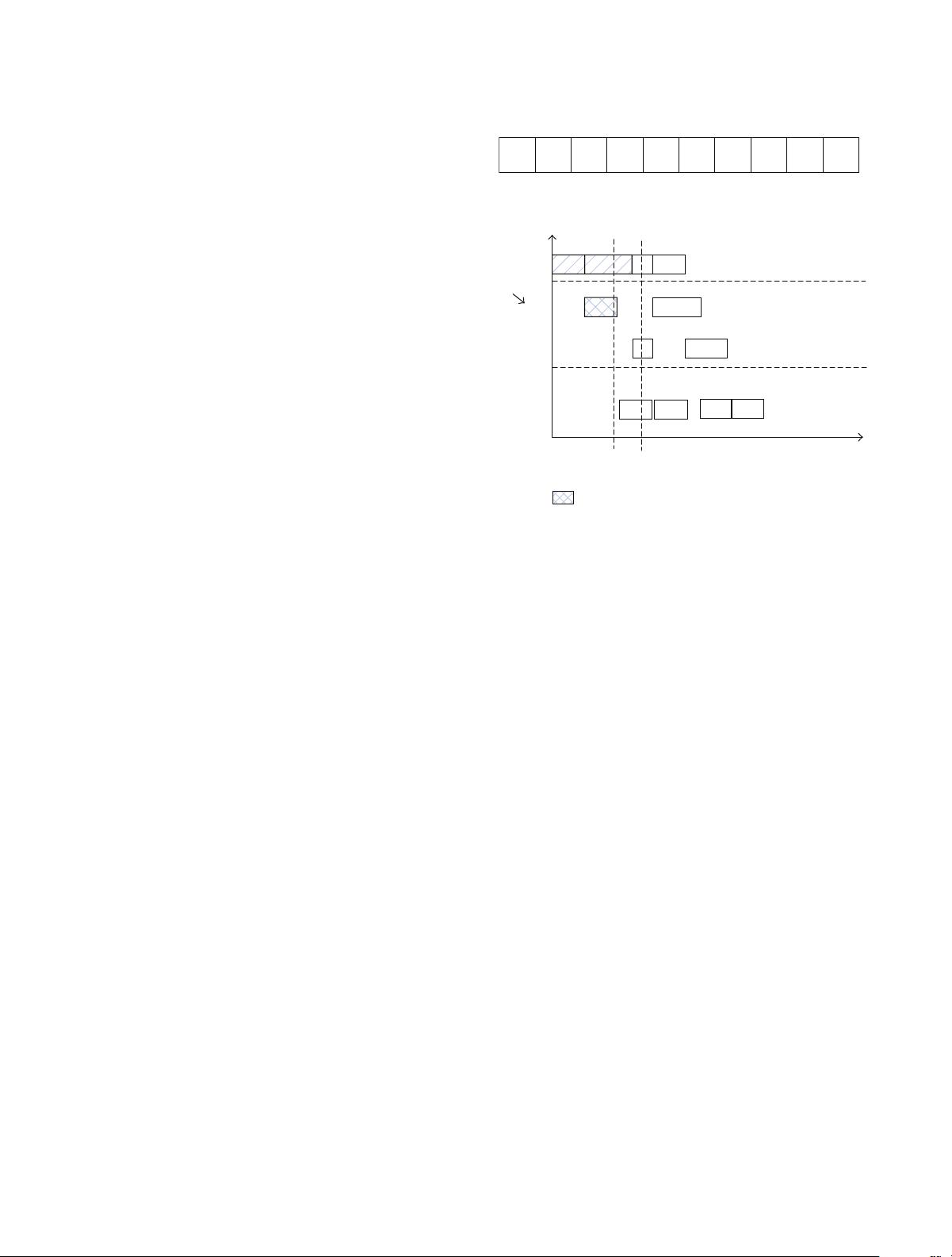
F : Situation of PM activity.
and three stages, Figure gives one solution representation,
where the scheduling sequence is
2
,
3
,...,and
7
.
e sequence in Figure is only for the rst stage; that
is, at the rst stage, each job is scheduled according to the
above sequence, while for the following stages, the decoding
mechanism is given as follows.
4.2. Decoding without Disruption. Itcanbeseenfromtheso-
lu-tion representation that the machine selection is not in-
cluded in the solution representation. e decoding for the
above solution representation is given as follows.
Step 1. For the rst stage, each job is scheduled according to
their sequence in the solution representation. In Figure the
rst job to be scheduled is
2
and the last one is
7
.Eachjob
selects the rst available machine.
Step 2. In the following stages, each job is to be scheduled just
aer its completion of the previous stage, and select the rst
available machine from the candidate machines.
4.3. Decoding with PM Activity. When considering the PM
activity, that is, at time , there is a PM activity occurring on
agivenmachine
𝑘
. en two situations we should consider,
that is, the rst is that when an operation is just being pro-
cessed on
𝑘
when the disruption event occurs. e second
situation is that the aected machine
𝑘
is idle and no op-
eration is aected by the PM activity.
(1)Situation 1. For the rst situation, an operation is aected
by the PM activity. Figure gives the example chart for the
situation. From Figure ,wecanseethat,attimepoint
1
,the
machine
2
shows a PM activity. It will restart its work at









