2022年JSSC定制集成电路特辑：频率锁定振荡器与高效能模数转换器

需积分: 10 117 浏览量更新于2024-06-28 收藏 124.88MB PDF 举报

"JSSC 2022.03 特别关注了2021年定制集成电路会议，包含多篇专题论文，涉及频率锁定振荡器、快速启动晶体振荡器、高精度分数-N合成器以及带隙基准电压源等领域的技术创新。" 在JSSC 2022.03的特辑中，主要探讨了集成电路设计的最新进展，特别是针对2021年定制集成电路会议中的创新技术。这个特辑由M.S. Oude Alink和F. Sheikh编辑，旨在展示过去一年在集成电路领域的重要成果。首先，一篇题为“使用复阻抗IQ平衡的频率锁定振荡器”的论文介绍了新的振荡器设计方法，通过复杂的RC阻抗实现频率锁定，以提高频率稳定性和性能。接着，文章“22nm FinFET CMOS工艺中基于阻抗引导的啁啾注入的快速启动晶体振荡器”探讨了一种采用先进工艺技术的高速启动振荡器，利用阻抗引导的啁啾注入来改善启动速度和频率精度。此外，还有一篇关于“3.2GHz、405fsrms抖动-237.2dB FoM的JITRing基分数-N合成器”的研究，展示了高精度的频率合成技术，该技术有望在无线通信和其他需要高频率稳定性的应用中发挥重要作用。论文“基于摆动增强浮动反相放大器的4-μW带宽/功率可扩展Δ-Σ调制器”提出了低功耗、高性能的模拟数字转换器设计，该设计通过优化摆动增强浮动反相放大器实现了功耗与带宽的可扩展性。接着，“具有树状搜索开关和160MHz能力的包络跟踪电源调制器”提出了新的电源管理解决方案，利用树状搜索技术提升调制器的效率和带宽。最后，一篇名为“103-dBSFDR无校准过采样SAR ADC的失配误差消除”的论文解决了模拟到数字转换器（ADC）中的失配问题，提出了一种无需校准即可实现高分辨率转换的方法。这些论文深入探讨了集成电路设计的关键技术，包括振荡器设计、频率合成、低功耗模拟电路和电源管理，为未来集成电路的发展提供了重要的理论和技术支持。

686 IEEE JOURNAL OF SOLID-STATE CIRCUITS, VOL. 57, NO. 3, MARCH 2022

achieves better energy-per-cycle performance (0.89 pJ/Cycle)

than does φ

operation (1.26 pJ/Cycle). Fig. 18(b) shows total

power consumption of the design from −40

◦

Cto80

◦

demonstrating a maximum power consumptio n increase of

∼10% at 80

◦

C due to the PTAT current source.

C. Comparison and Discussion

A performance and feature comparison of this work with

related state-of-the-art low-power FLL-based RC oscillators is

shown in Table I, which highlights the competitive energy-

per-cy cle power efﬁciency achievable with the presented

approach. Further reduction in power consumption may be

achievable through further optimization of VCO and frequency

divider design, which dominate static power consumption [see

Fig. 18(a)], or by using a lower dividing ratio (e.g., 8 versus

16). The technique should also provide improved performance

at more advanced process nodes compared to the 0.18-μm

CMOS prototype.

The theoretical performance of the IQ-balanced FVC is

similar to that of fully-passive FVC approaches. However,

the performance of the oscillator as implemented, including

accuracy and line sensitivity, is limited by the designed readout

circuit and could be improved in future implementations.

As is also shown in the table, the φ

−22.5

mixing phase case

performs less well in frequency sensitivity performance across

both temperature and supply voltage, which is due to a higher

operating frequency that is more sensitive to phase variation in

the source follower stage. This degradation can be improved

by increasing power consumption of the source follower.

While circuit area is comparable to many other approaches,

this can be further reduced by placing active devices under

higher m etal layer MIM capacitors, not done in this prototype,

or by u sing a switched-capacitor design to implement the high-

time-constant ﬁlter while reducing the capacitor value.

V. C

ONCLUSION

In this work, we have presented a fully-integrated RC

oscillator architectu re that uses an RC impedance IQ-b alanced

FLL. By detecting the error o f real and imaginary components

of an RC reference impedance, the FLL can be locked into

the pole frequency where both parts are balanced. Using this

architecture, the output frequency can also be changed using

a selectable phase shift instead of a control voltage, enabling

supply-invariant reconﬁgurability of the FLL frequency.

A prototype IC using this FLL architecture was imple-

mented in a 0.18-μm CMOS process and achieves a tem-

perature stability of 22 ppm/

◦

C with a nominal frequency of

647 kHz, and 34 ppm/

◦

C with a nominal frequency of 1.4 MHz

from −40

◦

Cto80

◦

C. Long-term stability of 10 ppm Allan

deviation is shown at 647 kHz while consuming only 820 nW.

While the theoretical performance of the IQ-balanced FVC

is similar to that of fully-passive FVCs, overall performance of

the implemented oscillator is limited by the designed readout

circuit and could be improved in future implementations.

As demonstrated, however, this approach provides an alter-

native approach for implementing active FVCs with recon-

ﬁgurable frequency output for low-frequency, fully-integrated

on-chip frequency references.

EFERENCES

[1] Y. Pu et al.,“A9-mm

ultra-low-power highly integrated 28-nm CMOS

SoC for Internet of Things,” IEEE J. Solid-State Circuits, vol. 53, no. 3,

pp. 936–948, Mar. 2018.

[2] S. Bose, B. Shen, and M. L. Johnston, “A batteryless motion-adaptive

heartbeat detection system-on-chip powered by human body heat,” IEEE

J . Solid-State Circuits, vol. 55, no. 11, pp. 2902–2913, Nov. 2020.

[3] D. Rufﬁeux, A. Pezous, A.-C. Pliska, and F. Krummenacher , “Silicon-

resonator-based, 3 μA real-time clock with ±5 ppm frequency accu-

racy,” in IEEE ISSCC Dig. Tech. Papers, Feb. 2009, pp. 210–211.

[4] S. Zaliasl et al., “A 3 ppm 1.5×0.8 mm

1.0 μA 32.768 kHz

MEMS-based oscillator,” IEEE J . Solid-State Cir cuits, vol. 50, no. 1,

pp. 291–302, Jan. 2015.

[5] U. Denier, “Analysis and design of an ultralow-power CMOS relaxation

oscillator ,” IEEE Tr ans. Circuits Syst. I, Reg. Papers, vol. 57, no. 8,

pp. 1973–1982, Aug. 2010.

[6] A. Paidimarri, D. Grifﬁth, A. Wang, A. P. Chandrakasan, and G. Burra,

“A 120 nW 18.5 kHz RC oscillator with comparator offset cancellation

for ±0.25% temperature stability,” in IEEE ISSCC Dig. Tech. Papers,

Feb. 2013, pp. 184–185.

[7] Y. Cao, P. Leroux, W. De Cock, and M. Steyaert, “A 63,000 Q-factor

relaxation oscillator with switched-capacitor integrated error feedback,”

in IEEE ISSCC Dig. Tech. Papers, Feb. 2013, pp. 186–187.

[8] Y.-H. Chiang and S.-I. Liu, “A submicrowatt 1.1-MHz CMOS relaxation

oscillator with temperature compensation,” IEEE Trans. Circuits Syst. II,

Exp. Briefs, vol. 60, no. 12, pp. 837–841, Dec. 2013.

[9] K.-J. Hsiao, “A 32.4 ppm/

◦

C 3.2–1.6 V self-chopped relaxation oscillator

with adaptiv e supply generation,” in Proc. Symp. VLSI Circuits (VLSIC),

2012, pp. 14–15.

[10] P. M. Nadeau, A. Paidimarri, and A. P. Chandrakasan, “Ultra low-energy

relaxation oscillator with 230 fJ/cycle efﬁciency,” IEEE J. Solid-State

Circuits, vol. 51, no. 4, pp. 789–799, Apr . 2016.

[11] M. Choi, T. Jang, S. Bang, Y. Shi, D. Blaauw, and D. Sylvester,

“A 110 nW resistive frequency locked on-chip oscillator with

34.3 ppm/

◦

C temperature stability for system-on-chip designs,” IEEE

J . Solid-State Circuits, vol. 51, no. 9, pp. 2106–2118, Sep. 2016.

[12] K. Pappu, G. P. Reitsma, and S. Bapat, “Frequency-locked-loop ring

oscillator with 3 ns peak-to-peak accumulated jitter in 1 ms time window

for high-resolution frequency counting,” in IEEE ISSCC Dig. Tech.

Papers, Feb . 2017, pp. 92–93.

[13] P. Chen, D. Li, Z. Yu, Q. Jin, and K. Yang, “A 0.84 pJ/cycle wheatstone

bridge based CMOS RC oscillator with reconﬁgurable frequencies,” in

Proc. IEEE Custom Integr. Circuits Conf. (CICC), Apr. 2019, pp. 1–4.

[14] A. Khashaba, J. Zhu, M. Ahmed, N. Pal, and P. K. Hanumolu, “A 34 μW

32 MHz RC oscillator with ±530 ppm inaccuracy from −40

◦

Cto85

◦

and 80 ppm/V supply sensiti vity enabled by pulse-density modulated

resistors,” in IEEE ISSCC Dig. Tech. Papers, Feb. 2020, pp. 66–68.

[15] J. Lee, P. Park, S. Cho, and M. Je, “A 4.7 MHz 53 μW fully differential

CMOS reference clock oscillator with −22 dB worst-case PSNR for

miniaturized SoCs, ” in IEEE ISSCC Dig. Tech. Papers, Mar. 2015,

pp. 1–3.

[16] M. Ding et al., “A 0.7-V 0.43-pJ/cycle wakeup timer based on a bang-

bang digital-intensive frequency-lock ed-loop for IoT applications,” IEEE

J . Solid State Circuits Lett., v ol. 1, no. 2, pp. 30–33, Feb. 2018.

[17] M. Ding, Z. Zhou, S. Traferro, Y.-H. Liu, C. Bachmann, and

F. Sebastiano, “A 33-ppm/

◦

C 240-nW 40-nm CMOS wakeup timer

based on a bang-bang digital-intensi ve frequency-locked-loop for IoT

applications,” IEEETrans.CircuitsSyst.I,Reg.Papers, vol. 67, no. 7,

pp. 2263–2273, Jul. 2020.

[18] T. Jang, M. Choi, S. Jeong, S. Bang, D. Sylvester, and D. Blaauw,

“A 4.7 nW 13.8 ppm/

◦

C self-biased wakeup timer using a switched-

resistor scheme,” in IEEE ISSCC Dig. Tech. Papers, Jan. 2016,

pp. 102–103.

[19] G. Zhang, K. Yayama, A. Katsushima, and T. Miki, “A 3.2 ppm/

◦

second-order temperature compensated CMOS on-chip oscillator using

voltage ratio adjusting technique,” IEEE J. Solid-State Circuits, vol. 53,

no. 4, pp. 1184–1191, Apr. 2018.

[20] C. Gürleyük, L. Pedalà, S. P an, F. Sebastiano, and K. A. A. Makinwa,

“A CMOS dual-RC frequency reference with ±200-ppm inaccuracy

from −45

◦

Cto85

◦

C,” IEEE J. Solid-State Circuits, vol. 53, no. 12,

pp. 3386–3395, Dec. 2018.

SHEN et al. : FREQUENCY-LOCKED OSCILLATOR USING COMPLEX RC IMPEDANCE IQ-BALANCING 687

[21] J. Jung, I.-H. Kim, S.-J. Kim, Y. Lee, and J.-H. Chun, “A 1.08-nW/kHz

13.2-ppm/

◦

C self-biased timer using temperature-insensitive resistive

current,” IEEE J. Solid-State Circuits, vol. 53, no. 8, pp. 2311–2318,

Aug. 2018.

[22] D. S. Truesdell, A. Dissanayak e , and B. H. Calhoun, “A 0.6-V

44.6-fJ/cycle energy-optimized frequency-locked loop in 65-nm CMOS

with 20.3-ppm/

◦

C stability,” IEEE Solid-State Circuits Lett.,vol.2,

no. 10, pp. 223–226, Oct. 2019.

[23] J. Lee, A. K. George, and M. Je, “An ultra-low-noise swing-boosted

differential relaxation oscillator in 0.18-μmCMOS,”IEEE J. Solid-State

Circuits, vol. 55, no. 9, pp. 2489–2497, Sep. 2020.

[24] B. Shen and M. L. Johnston, “A digitally-reconﬁgurable RC frequenc y

generator using impedance IQ-balanced frequency-locked-loop with

selectable phase mixing,” in Proc. IEEE Custom Integr. Circuits Conf.

(CICC), Apr. 2021, pp. 1–2.

[25] W. Riley and D. Howe. (2008). Handbook of Frequency Stabil-

ity Analysis. Jul. 1, 2008. [Online]. Available: https://tsapps.nist.gov/

publication/get_pdf.cfm?pub_id=50505

[26] E. Vittoz and J. Fellrath, “CMOS analog integrated circuits based on

weak inv ersion operations,” IEEE J. Solid-State Circuits, vol. JSSC-12,

no. 3, pp. 224–231, Jun. 1977.

[27] H. J. Oguey and D. Aebischer, “CMOS current reference without

resistance,” IEEE J. Solid-State Circuits, vol. 32, no. 7, pp. 1132–1135,

Jul. 1997.

[28] I. Lee, D. Sylvester, and D. Blaauw, “A constant ener gy-per -cycle ring

oscillator over a wide frequency range for wireless sensor nodes,” IEEE

J . Solid-State Circuits, vol. 51, no. 3, pp. 697–711, Mar. 2016.

Boyu Shen (Member, IEEE) receiv ed the B.S.

degree in electronic science and technology from

the University of Science and Technology of China

(USTC), Hefei, China, in 2015, and the Ph.D. degree

in electrical and computer engineering from Oregon

State Uni versity , Corvallis, OR, USA, in 2020.

From September 2019 to March 2020, he was with

Velodyne Lidar Inc., San Jose, CA, USA, where

he has worked as an Analog Design Intern on the

de velopment LiDAR transmitters. He is currently a

Design Engineer focusing on sensing circuits and

systems with Kilby Labs, Texas Instruments, Dallas, TX, USA. His research

interests include analog and mixed-signal circuits and systems design for

optical and biomedical sensing applications.

Soumya Bose (Member, IEEE) receiv ed the B.E.

degree in electronics and telecommunication engi-

neering from the Indian Institute of Engineering

Science and Technology (IIEST) Shibpur, Howrah,

India, in 2009, the M.Tech. degree from IIT Kharag-

pur, Kharagpur , India, in 2013, and the Ph.D. degree

in electrical and computer engineering from Oregon

State Uni versity , Corvallis, OR, USA, in 2019.

From 2013 to 2015, he was with Rambus, Ben-

galuru, India, working on high-speed memory inter-

faces for multi-protocol PHYs. From May 2018 to

August 2018, he was with Kilby Labs, Texas Instruments, Dallas, TX, USA,

where he has worked on ultralow quiescent current low-dropout (LDO)

regulators. Since 2019, he has been working with Intel Corporation, Hillsboro,

OR, USA, where he is currently a Research Scientist with Intel Labs.

His research interests include integrated circuit design for analog signal

processing, biomedical sensing, wearable system-on-chips, energy harvesting,

power management, and high-speed interconnects.

Dr. Bose received the Center for Design of Analog-Digital Integrated Cir-

cuits (CDADIC) Best Poster Award in 2017. He also serves as a Reviewer for

the IEEE J

OURNAL OF SOLID-STATE CIRCUI TS, the IEEE TRANSACTIONS

ON BIOMEDICAL CI RCUITS AND SYS TEMS, the IEEE TRANSACTI ONS ON

CIRCUI TS AND SYSTEMS—I: REGULAR PAP ERS, and the IEEE TRANS AC-

TIONS ON CIRCUITS AND SYSTEMS—II: EXPRES S BRIEFS.

Matthew L. Johnston (Senior Member, IEEE)

received the B.S. degree in electrical engineer-

ing from the California Institute of Technology ,

Pasadena, CA, USA, in 2005, and the M.S.

and Ph.D. degrees in electrical engineering from

Columbia University, New York, NY, USA, in

2006 and 2012, respectively.

He was a Co-Founder and the Manager of

Research with Helixis, Carlsbad, CA, USA,

a Caltech-based spinout developing instrumentation

for real-time DNA ampliﬁcation, from 2007, to its

acquisition by Illumina, San Diego, CA, USA, in 2010. From 2012 to 2013,

he was a Post-Doctoral Scholar with the Bioelectronic Systems Laboratory,

Columbia University, and an Associate with Ascent Biomedical Ventures,

New York. In 2014, he joined Oregon State University, Corvallis, OR, USA,

where he is currently an Associate Professor with the School of Electrical

Engineering and Computer Science. His current research interests include

the integration of sensors and transducers with silicon integrated circuits,

stretchable circuits and sensor systems, lab-on-CMOS platforms, bio-energy

harvesting, and low-po wer distributed sensing.

Dr. Johnston was the recipient of the 2020 Semiconductor Research Corpo-

ration (SRC) Young Faculty Award, the 2021 Oregon State Unive rsity College

of Engineering Faculty Teaching Excellence Award, and the 2021 Oregon

State University Provost Fellowship. He is an Associate Editor of the IEEE

RANSACTIONS ON BIOMEDICAL CIRCUI TS AND SYSTEMS and the IEEE

PEN JOURNAL OF CIRCUITS AND SYSTEMS.HealsoservesontheBio-

medical and Life Science Circuits and Systems Technical Committee and

the Analog Signal Processing Technical Committee of the IEEE Circuits and

Systems Society.

688 IEEE JOURNAL OF SOLID-STATE CIRCUITS, VOL. 57, NO. 3, MARCH 2022

A Fast Startup Crystal Oscillator Using Impedance

Guided Chirp Injection in 22 nm FinFET CMOS

Hao Luo , Member, IEEE, Somnath Kundu, Timo Huusari, Sarah Shahraini, Member, IEEE, Eduardo Alban,

Jason Mix, Nasser Kurd, Mohamed Abdel-Moneum, Senior Member, IEEE, and Brent Carlton, Member, IEEE

Abstract—An Impedance Guided Chirp Injection (IGCI)

oscillator-based fast startup technique is proposed in this work

demonstrating startup time between 5 and 100 µsacrossa

wide range of oscillator frequencies. The IGCI technique can

efﬁciently detect the resonance frequency of the crystal and

provide energy injection for fast crystal startup. The simplicity

of the implementation of the IGCI circuitry enables easy porting

across technology nodes and interfacing with different oscillator

topologies. Compared to previous negative resistance boosting

or open-loop injection techniques, the proposed IGCI achieves

both faster startup and lower injection power which reduces the

overall startup energy. A test chip is fabricated in Intel 22FFL

technology and the measurements are performed using 38.4 MHz

crystal achieving ∼2.6× faster startup than normal startup

(with same biasing, load cap) without any injection. Extensive

measurements are performed across different temperatures and

multiple startup occurrences.

Index Terms— Chirp injection, crystal oscillator (XO), fast

startup.

I. INTRODUCTION

OW power mobile and edge computing systems require

fast wakeup for pleasant, responsive end-user experi-

ence and for efﬁcient data processing. Fast startup oscillators

are needed to en able the system to periodically go into its

sleep state and wakeup fast enough to be within the low

power states’ allowed latency transitions [1]. If the reference

oscillator cannot reach the performance state target frequency

stability and swing within the state exit latency tim e, the

oscillator needs to be kept always on or at least go into a

reduced swing state. Fig. 1 is a represen tation of the logic

power state transitions and the relative power savings of the

reference oscillator between switching from active state to

reduced swing state versus the totally

OFF state that can only

be enabled by the fast startup capability. The transition speed

between these states is limited by th e startup time of reference

crystal oscillator. Due to the resonators’ extremely high-quality

factor (Q = 10

–10

), the oscillators’ startup speed is very

slow. For instance, a 10’s of MHz crystal oscillator, with

reasonable power consumption, may take several milliseconds

to turn on and settle to its ﬁnal steady-state frequency [2 ]–[7].

Manuscript received July 16, 2021; revised September 18, 2021,

October 27, 2021, October 29, 2021, and December 3, 2021; accepted

December 10, 2021. Date of publication December 31, 2021; date of current

version February 24, 2022. This article was approv ed by Associate Editor

Mark Oude Alink. (Corresponding author: Hao Luo.)

The authors are with Intel Corporation, Santa Clara, CA 95054 USA (e-

mail: hao.luo@intel.com).

Color versions of one or more ﬁgures in this article are available at

https://doi.org/10.1109/JSSC.2021.3136237.

Digital Object Identiﬁer 10.1109/JSSC.2021.3136237

Fig. 1. SoC power transitioning from sleep state to active state and the

corresponding reference oscillator po wer in reduced swing mode and total off

mode enabled by fast startup.

For a linear oscillator model with a resona tor’s quality factor

of Q and resonance frequency o f ω

, the startup time is [8]

start

∝



1 + R



· ln



init



(1)

where R

and R

are the negative resistance provided by

the active circuit and the resonator’s motional loss resistance,

respectively. I

is the ﬁnal steady-state motion current in the

resonator and I

init

is the initial motion current, which, in a

normal starting case, is deter mined by th e thermal noise inside

the system. This equation indicates that the startup time is long

for a high Q crystal. On the other hand, such high Q crystal

resonators are desired to reduce the oscillator jitter and power.

Equation (1) also points out that increasing the R

or I

init

may

effectively reduce T

start

Oscillator startup time improvement techniques such as

negative resistance (R

) boosting [10], [17] or external energy

injection [9], [11]–[16] have demonstrated sub-100 μsstartup

time. To boost R

, either a large bias current or multiple am pli-

fying stages with dynamic load cap adjusting are required.

External energy injection at the start phase to increase I

init

also proven to be highly efﬁcient. However, the large Q of

the resonator poses challenges in injecting power precisely at

the resonance frequency ( f

). Therefore, frequency chirp [11]

and dithering [15], [19] techniq ues are used. Still, they pro-

vide a suboptimal solution since chirping requires a search

operation to cover the entire frequency range and dithering

spreads the energy over a wide sp ectrum, both of which result

in a signiﬁcant wastage in startup time and energy. Self-

timed injection [9], [20] or phase-locked loop (PLL) assisted

See https://www.ieee.org/publications/rights/index.html for more information.

LUO et al.: FAST STARTUP OX USING IGCI IN 22 nm FinFET CMOS 689

accurate injection [13] can match the injected frequency with

the resonator frequency and thus achieve very fast startup.

However, because the I

init

is still very small at beginning of the

oscillation, it requires a high-gain and high-speed comparator

to detect the phase. [20] uses a dynamic comparator. However,

the phase detection can be delayed by the comparator’s clock

(200 MHz–2 GHz). To achieve the desired I

init

quickly, [9]

disables the load capacitors during startup which may not

be an option in practical implementations where capacitors

are placed on-board . Similarly [13] relies on an initial in jec-

tion using the voltage-controlled-oscillator (VCO) inside PLL

with a <5000 ppm error which requires process-voltage-

temperature (PVT) calibration. Synchronized signal injection

(SSI) [16] and multi-phase signal injection (MPSI) [21] re-

align the injection phase after a number of cycles of injection.

It does not accumulate the phase error to a point where it

starts to be an antiphase of the crystal resonance. However,

since they did not address the issue of matching the injection

frequency to the crystal, it may still need calibration or have

a wide variation of startup time across PVT.

To optimize the injection efﬁciency an d hence startup time,

a potential robust impedance guided chirp injection (IGCI)

frequency locking technique for fast startup of reference

oscillators is demonstrated in an Intel 22FFL test chip achiev-

ing a 2.6× reduction in startup time at 38.4 MHz [18].

It can automatically track the resonator frequency without

using any high-power or high-speed supporting circuits. The

concept of the proposed IGCI based fast startup and its

analysis are described in Sections II and III respectively.

The implementation details are illustrated in Section IV. Test-

chip measurement results and conclusion is presented in

Sections V and VI, respectively.

II. P

ROPOSED FAST STARTUP CONCEPT

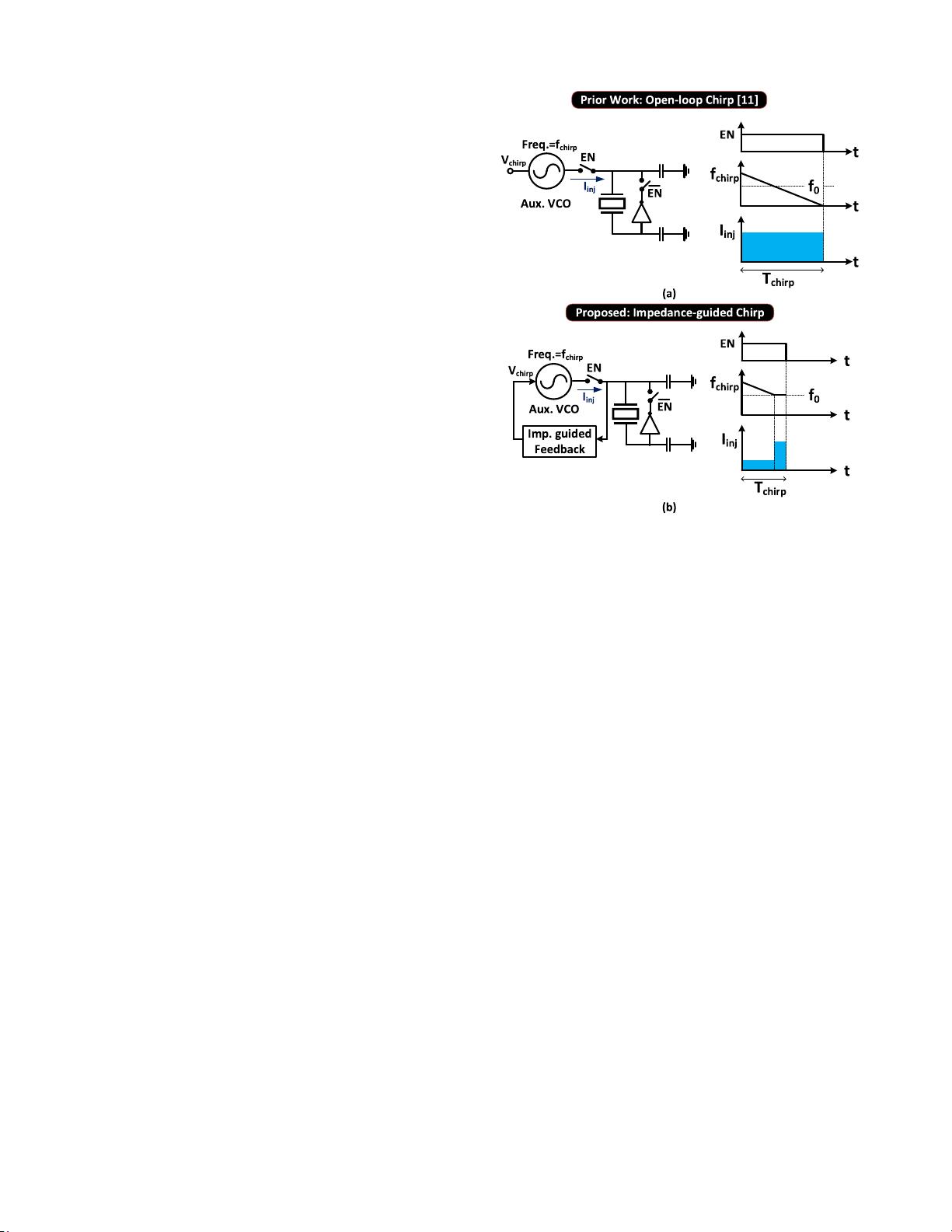
Fig. 2 explains the concept of the proposed fast startup

circuit using IGCI while comparing it with the previous work

on open-loop chirp injection-based fast startup [11]. Since it

is impossible to precisely align the frequency of the auxiliary

VCO, used for energy injection, with the resonance frequency

( f

) of the crystal under PVT variations, a frequency chirp

( f

chirp

) can be used to cover this frequency variation. When

chirp

matches f

, initial motional current (I

init

) is developed

inside the crystal which provides faster startup. From (1), it is

evident that higher I

init

reduces T

start

. However, in an open-

loop chirp injection [Fig. 2(a)] h igher I

init

would require either

slower chirp, increasing the chirp duration (T

chirp

), o r higher

current injection (I

inj

) since startup energy (E

start

) is propor-

tional to T

chirp

× I

inj

(injection period) + T

grow

× I

bias

(self-

oscillation growing period). This results in an increase in E

start

In order to achieve sufﬁciently high I

init

while minimizing

start

, an impedance-guided feedback mechanism is utilized

in this work, as shown in Fig. 2(b). This feedback network

detects the impedance change in the crystal by observing the

voltage across its terminals. At the beginning f

chirp

> f

and a small I

inj

is applied at the crystal. As f

chirp

sweeps

down and approaches f

, the crystal motional current increases

signiﬁcantly, and the voltage across the crystal drops. This is

Fig. 2. Concept of (a) conventional open-loop chirp injection and (b) pro-

posed IGCI-based fast startup.

detected by the feedback network, which then holds f

chirp

and applies high I

inj

for a ﬁxed duration until I

init

reaches I

At this point, the fast startup circuit is disab led and the main

oscillator driver takes over driving the crystal. This techn ique

utilizes a narrower chirp range (smaller T

chirp

) and low I

inj

during the frequency search operation, which both signiﬁcantly

reduce E

start

(=T

chirp

× I

injsmall

+ T

lock

× I

inj

+ T

grow

× I

bias

)

compared to conventional open-loop chirp.

The key building blocks inside the IGCI circuit and their

transient behavior are shown in Fig. 3. An envelope detector

measures the voltage amplitude across the crystal. Its output,

Env, is then compared with a reference, V

ref

.Thevalueof

ref

is determined from the minimum droop that is a function

of crystal properties and other design parameters explained in

Section III. When f

chirp

approaches f

, it causes Env to drop.

It is detected by the comparator which holds (Hold = 1) the

chirp generator output (V

chirp

). The state machine inside the

logic block increases the injection drive strength (Boost = 1)

of the dual-strength driver to high I

inj

for a ﬁxed duration that

can be predetermined based on the load capacitor and crystal

characteristics [12].

The simulated transient behavior of the crystal motional

current (I

) during chirp injection and the voltage at the output

of the injection driver is shown in Fig. 4 which compares

the IGCI method with the open-loop chirp injection. During

the open-loop chirp, I

reaches its peak value when f

chirp

approaches f

and causes a voltage droop at the driver output.

Once f

chirp

passes f

, I

gradually reduces showing a ripple

effect. The IGCI circuit can detect this droop, hold f

chirp

,and

inject with a higher drive strength to substantially increase I

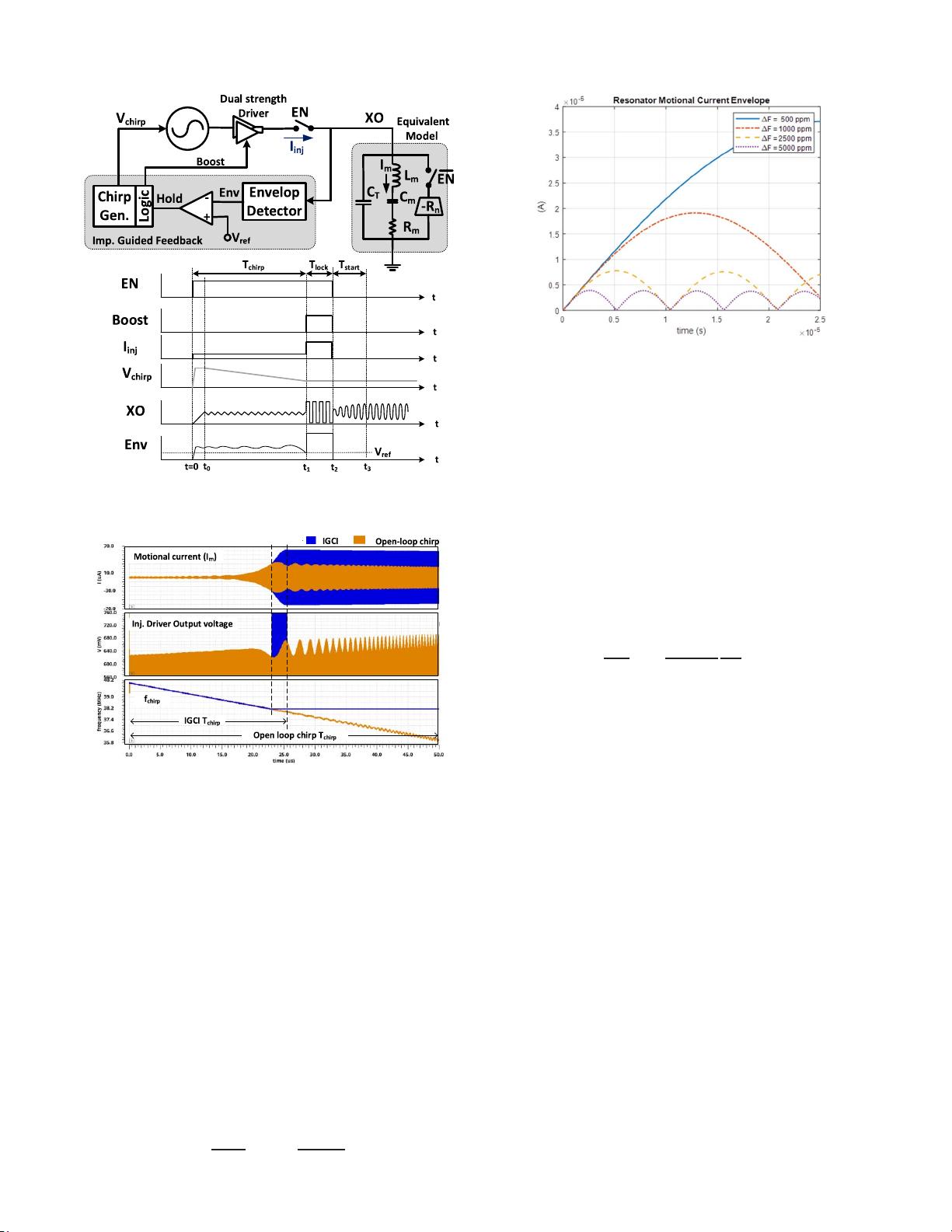
690 IEEE JOURNAL OF SOLID-STATE CIRCUITS, VOL. 57, NO. 3, MARCH 2022

Fig. 3. Simpliﬁed block diagram of an IGCI based fast startup circuit.

Fig. 4. IGCI procedure compared to open-loop chip injection.

III. SYSTEM ANALYSIS AND DESIGN CONSIDERATIONS

During the injection period, due to the high Q of the

resonator, only a fraction of the injected power within the

crystal narrow bandwidth near f

is coupled to the resonator.

The injected energy helps to build up the motional current

that increases with time. However, if there is any frequency

error (F =|f

chirp

- f

|), there will be a maximum value that

the motional current can reach [18]. The relationship between

the motional current and the frequency error is shown in

Fig. 5. When the frequency error is near zero (F ≈ 0),

the motional current can linearly increase with time since the

injected clock is always in phase with the oscillation and

the resonator keeps gaining energy in each cycle. The opti-

mum injection time is determined by the targeted steady-state

current [14]

opt

−2Q



1 −

π R

INJ



. (2)

Fig. 5. Motional current en velops for different injection frequency errors.

When there is frequency error (F = 0), the motional

current starts to decrease after it reaches a maximum value at

t = 1/2 F and the process repeats p eriodically every 1/F

cycle-shown as ripples. Energy starts bleeding away from

the resonator as the phase difference deviates from in-phase

to anti-phase. The op timum injection time becomes 1/2 F

(assuming the peak current is still less th an the targeted i

As explained earlier, one of the key metrics that lim its

the minimum injection time is F. For a given ratio of

injected voltage amplitude (V

INJ

) to oscillation voltage swing

), the m a ximum error toler ated while still achieving peak

amplitude is given by [14]

F

=±

INJ

/π

. (3)

Here C

is the crystal motional capacitance and C

the total effective load capacitance. The IGCI circuit must

detect f

within the required accuracy F/ f

. For example,

a design with V

INJ

= 1.0V,V

= 600 mV, and C

1/4000, the pierce oscillator requires ∼500 ppm injection

clock accuracy. There are several circuit non-idealities such

as sweep speed, noise, comparator offset, and delay in the

detection and injection circuitry that will affect the clock

detecting accuracy.

For a given crystal, there is an optimum driver impedance

S,opt

) which balances the voltage droop across the crystal

and the injection time constants or the driver bandwidth.

As shown in Fig. 6(a), a voltage divider b etween the source

resistance R

, which is the injection driver output impedance,

and the impedance of the crystal Z

(s) = R

+sL

+1/sC

with the load capacitan ces C

, determines the swing across

XO during the injection. When the injected frequency f

chirp

above or below f

, Z

appears as a high impedance and the

swing at XO becomes V

≈ V

INJ

/(1 + (2π f

chirp

)

1/2

assuming a sinusoidal input for simplicity. When f

chirp

≈ f

drops to the crystal’s motion loss resistance, R

, resulting

in V

≈ V

INJ

/(R

+ R

). Since the IGCI d etects the

change in V

as f

chirp

approaches f

, there is an optimum

value of R

that maximizes this change as evident from the

ac response plot for different R

in Fig. 6(a). For this work,

the optimum was around 400  for the 38.4 MHz crystal as

剩余311页未读，继续阅读

netshell

粉丝: 11
资源: 185

2022年JSSC定制集成电路特辑：频率锁定振荡器与高效能模数转换器

2022年JSSC特殊期刊：VLSI电路研讨会亮点

2022年2月信息技术期刊：毫米波收发器与射频SoC创新

2022 IEEE国际固态电路会议特刊：超低相位噪声X带BiCMOS VCO与数字PLL

JSSC 2022.06

JSSC 2022.09

JSSC 2022.01

JSSC 2022.04

JSSC 2022.11

JSSC 2022.10

JSSC 2022.02

最新资源