有限差分法：数值求解微分方程的计算机方法

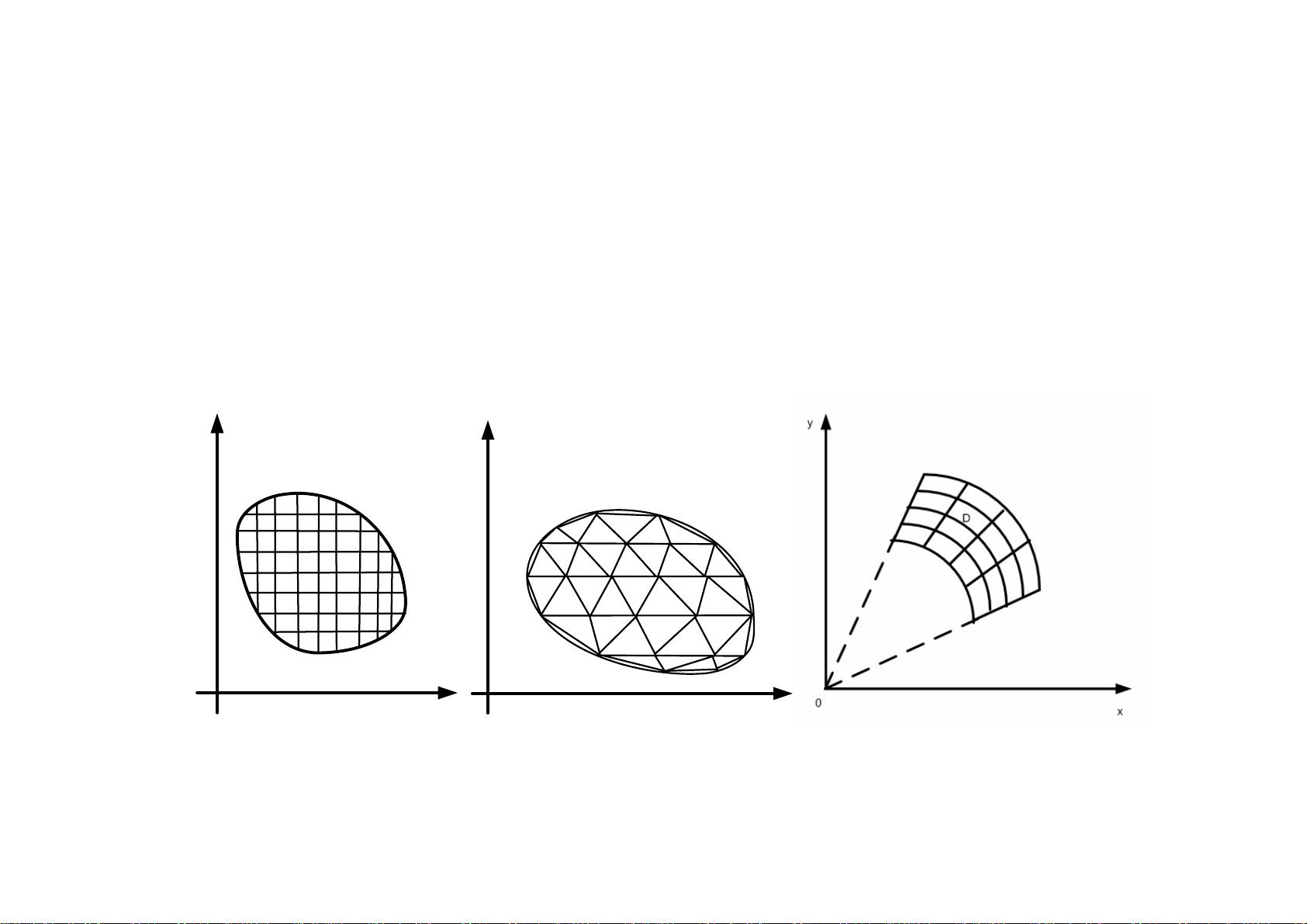
"有限差分法是数值计算中用于求解常微分方程和偏微分方程的一种方法，它通过将连续变量离散化，用差分近似微分，进而转换为求解差分方程组的问题。这种方法在计算机科学、数学和物理等领域有广泛应用，因其计算直观且程序设计简单。有限差分法的操作主要包括两个步骤：一是用差分代替微分，二是求解得到的差分方程组。在实际应用中，通常采用规则的网络分割，将函数定义域划分为多个子区域，并定义节点，以便于计算机处理。节点分为正则节点和非正则节点，前者所有相邻节点都在定义域内，后者则不然。在求解差分方程组时，需要在所有节点上找到离散近似值。一阶和二阶微商可以用相邻点的函数值差分来近似，例如一阶向前差分公式。步长h越小，近似精度越高。" 有限差分法的核心思想是将微分方程的解析解转化为数值解，这在处理复杂的物理问题时尤其有用，因为许多实际问题无法直接得出解析解。这种方法首先将连续空间分割成离散的网格，然后用每个网格点上的函数值来近似连续函数。差分是有限差分法中的基本操作，它模拟了微分的过程。例如，一阶前向差分公式 \( f'(x_i) \approx \frac{f(x_{i+1}) - f(x_i)}{h} \) 就是用函数在相邻点 \( x_i \) 和 \( x_{i+1} \) 上的值之差来估算 \( x_i \) 处的导数值。 在有限差分法中，差分格式的选择至关重要，因为它直接影响数值解的精度和稳定性。通常会根据微分方程的类型和边界条件选择合适的差分格式。对于偏微分方程，还需要考虑空间和时间的离散化，这可能导致更复杂的差分方程组。此外，为了提高计算效率和减少误差，有时会使用中心差分或其他高阶差分格式。 在求解差分方程组时，可能会采用迭代方法，如欧拉法、龙格-库塔法等，或者是直接求解线性系统的方法，如高斯消元法或迭代求解器。值得注意的是，为了确保数值解的稳定性和收敛性，需要合理选择步长h以及离散网格的布局。 有限差分法在工程、气象学、流体力学、地球科学和金融模型等多个领域都有广泛的应用。例如，在模拟热传导、流体流动、电磁波传播等问题时，有限差分法是一种常用的技术。然而，它也存在局限性，比如在处理具有复杂几何形状的区域或需要极高精度的场合，有限差分法可能不如其他数值方法（如有限元法或有限体积法）有效。因此，在实际应用中，需要根据问题的特点和计算资源选择最适合的数值方法。