浙江大学城市学院数据结构基础：约瑟夫环顺序与链式实现详解

约瑟夫环是一种经典的算法问题，源自于数学游戏，通常用于讲解循环列表的概念和操作。在浙江大学城市学院的数据结构基础课程实验六中，学生们被要求实现约瑟夫环的两种不同存储结构：顺序存储（数组）和链式存储（链表）。 1. **顺序存储结构（SeqList）**: - 使用`typedef`定义了`ElemType`和`SeqList`结构体，其中`SeqList`包含一个动态大小的元素数组`list`，整型变量`size`表示当前元素数量，以及最大容量`MaxSize`。 - 实现的重要函数包括： - `InitList(SeqList& L)`：初始化线性表，分配内存并设置初始状态。 - `LengthList(SeqList L)`：计算线性表的长度。 - `EmptyList(SeqList L)`：检查线性表是否为空。 - `FindList(SeqList L, ElemType item)`：查找给定值在列表中的位置。 - `GetList(SeqList L, int pos)`：获取指定索引位置的元素值。 - `DeleteList(SeqList& L, ElemType& item, int pos)`：根据给定位置删除元素。 在主函数中，通过循环和取模操作找到下一位被淘汰的人，并更新线性表。 2. **链式存储结构（LNode）**: - 定义了链表节点类型`LNode`，包含数据`data`和指向下一个节点的指针`next`。 - 对应的重要函数实现包括： - `InitList(LNode*& H)`：初始化单链表，创建一个空头节点。 - `LengthList(LNode* H)`：遍历链表计算其长度。 - `EmptyList(LNode* H)`：检查链表是否为空。 - `FindList(LNode* H, ElemType item)`：在链表中查找指定值的位置。 - `GetList(LNode* H, int pos)`：获取链表中指定位置的元素。 - `InsertList(LNode*& H, ElemType item, int pos)`：在链表的指定位置插入新元素。 这种结构的优势在于插入和删除操作的时间复杂度较低，但查找可能需要遍历整个链表。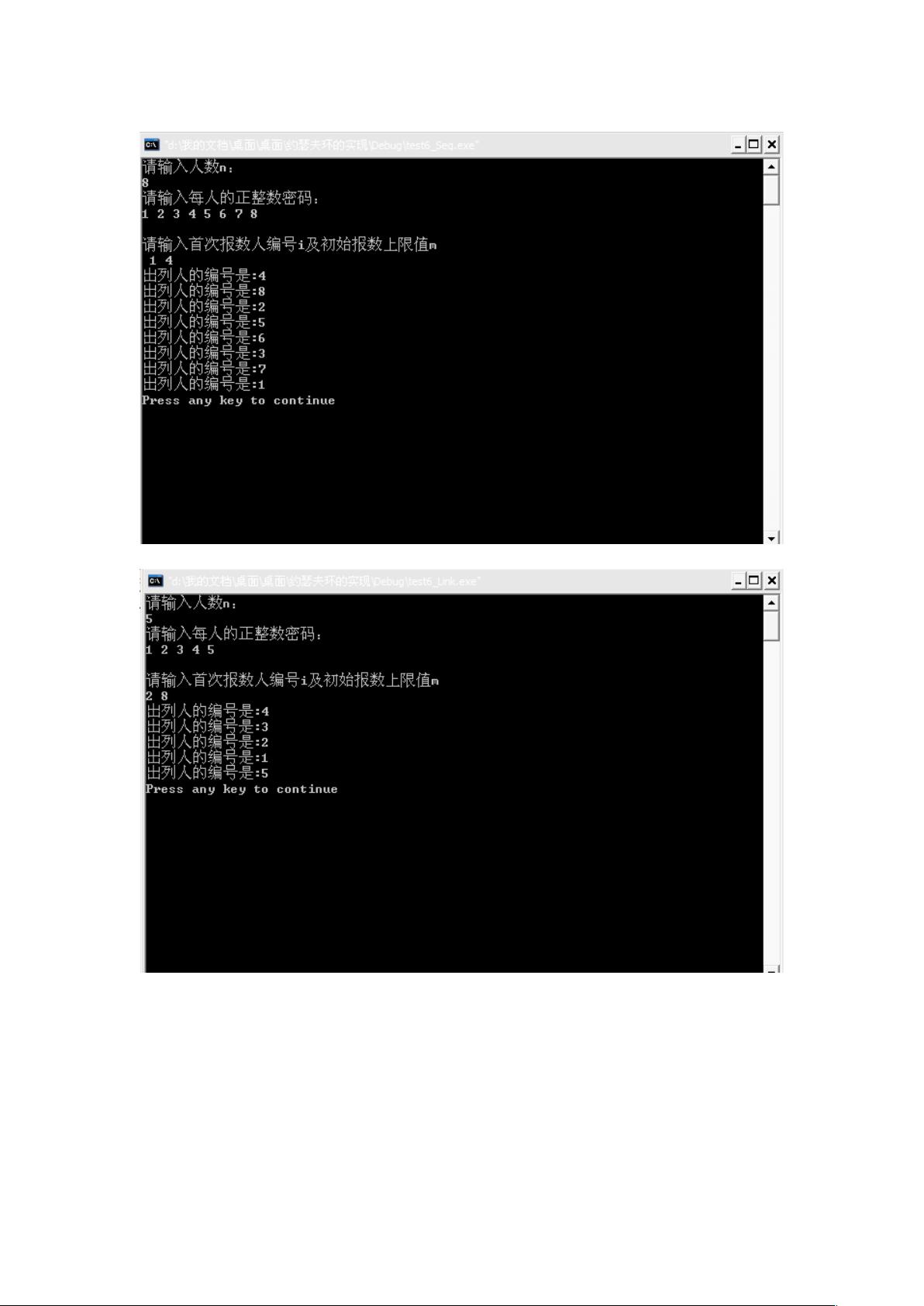 在约瑟夫环的实现过程中，主要步骤是： - 对于顺序存储，首先计算线性表的长度，然后根据报数规则找出下一个淘汰者的位置。 - 当位置为0时，表示淘汰者位于列表尾部，更新淘汰者的计数值`m`。 - 删除淘汰者，线性表长度减一，然后循环报数，直到只剩一人为止。 - 对于链式存储，同样执行上述步骤，但插入和删除操作更为灵活，但遍历整个链表以查找元素会增加时间开销。 实验的目标是让学生熟悉不同数据结构在实际问题中的应用，并理解如何根据问题需求选择合适的数据结构来优化算法效率。同时，这也有助于提高他们的编程能力和逻辑思维能力。