逻辑回归：极大似然估计详解与代价函数优化

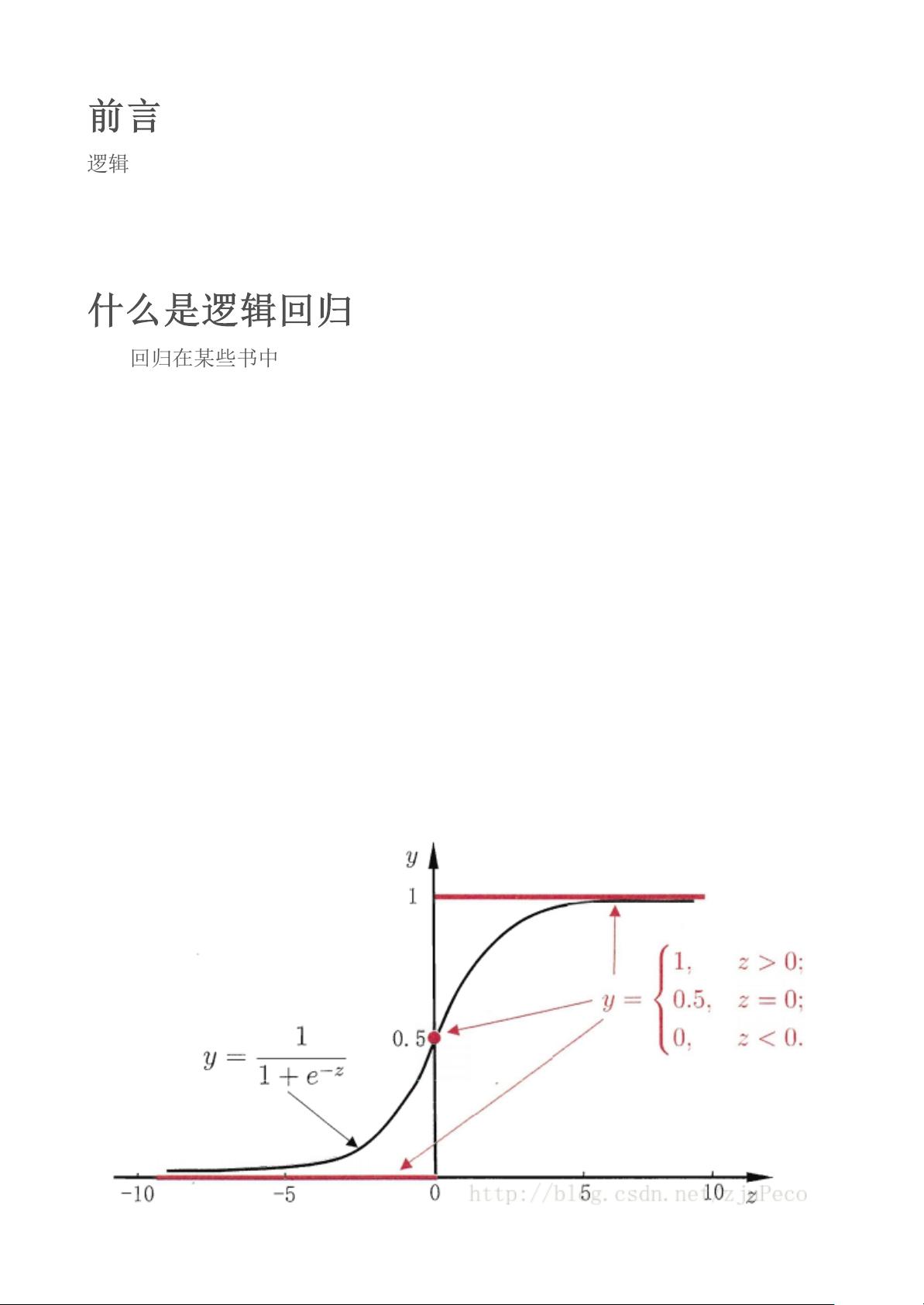
逻辑回归(logistic regression)是一种广泛应用在分类问题中的统计学方法，其核心在于通过线性模型预测二分类问题中的后验概率。它之所以被称为“回归”，是因为其最初的形式与线性回归相似，但实际上处理的是离散的类别输出。 逻辑回归的基本思想是将线性模型的输出（通常是连续的）通过Sigmoid函数（sigmoid function）映射到0到1之间，这使得输出值可以解释为类别1的概率。Sigmoid函数的公式为 \( \phi(z) = \frac{1}{1+e^{-z}} \)，它是一个平滑的、单调递增且连续可微的函数，完美地解决了理想阶跃函数（step function）的不连续问题。 对于每个样本点 \( (x_i, y_i) \)，其中 \( x_i \) 是输入特征向量，\( y_i \) 是对应的类别标签（0或1），逻辑回归的目标是找到一组权重 \( w \) 和偏置 \( b \)，使得模型预测 \( \phi(w^T x_i + b) \) 接近于真实类别概率。当 \( \phi(z_i) \geq 0.5 \) 时，预测为类别1，否则为类别0。 逻辑回归的代价函数，通常称为损失函数，选择模仿线性回归的均方误差并不适用，因为Sigmoid函数导致的输出是非线性的。为此，我们采用逻辑损失函数（log loss），也称为交叉熵损失函数（cross-entropy loss），其表达式为： \[ J(w) = -\frac{1}{m} \sum_{i=1}^{m} [y_i \log(\phi(z_i)) + (1 - y_i) \log(1 - \phi(z_i))] \] 这里，\( m \) 是样本数量。这个函数的特点是，当预测概率接近真实类别概率时，损失较小；反之，当预测与真实类别相反时，损失增大，从而鼓励模型学习更准确的决策边界。 优化逻辑回归模型的过程通常采用梯度下降法或其他优化算法，目标是找到参数 \( w \) 和 \( b \) 的最小值，以使得整体损失函数达到最优。在实际应用中，逻辑回归还可能进行正则化，以防止过拟合现象的发生。 逻辑回归通过结合线性模型和Sigmoid函数，巧妙地将连续的线性预测转换为类别决策，其代价函数的选择和优化策略确保了模型的有效性和稳定性，使其在众多分类任务中占据重要地位。