麦克斯韦方程解析与电磁场边界条件详解

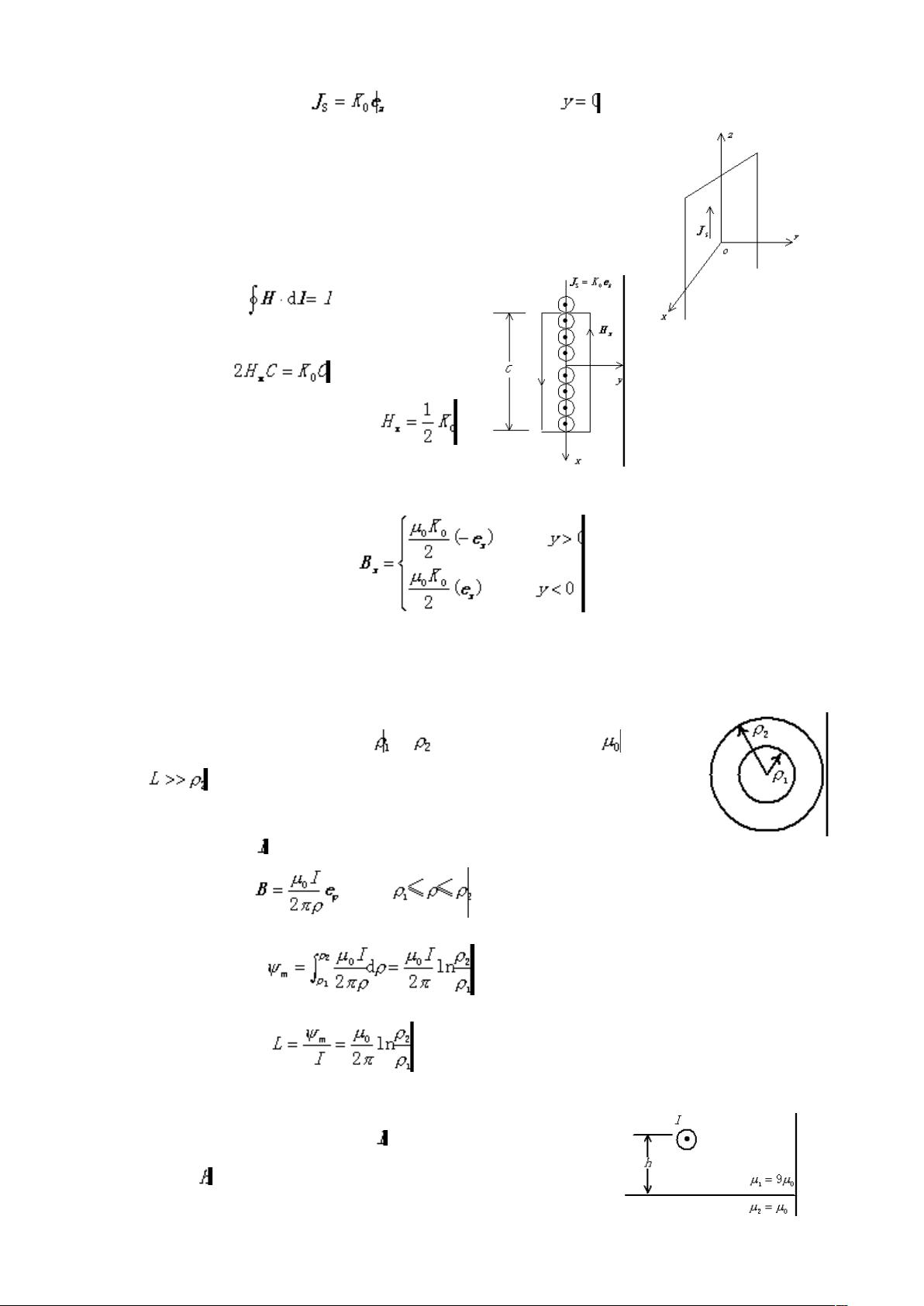
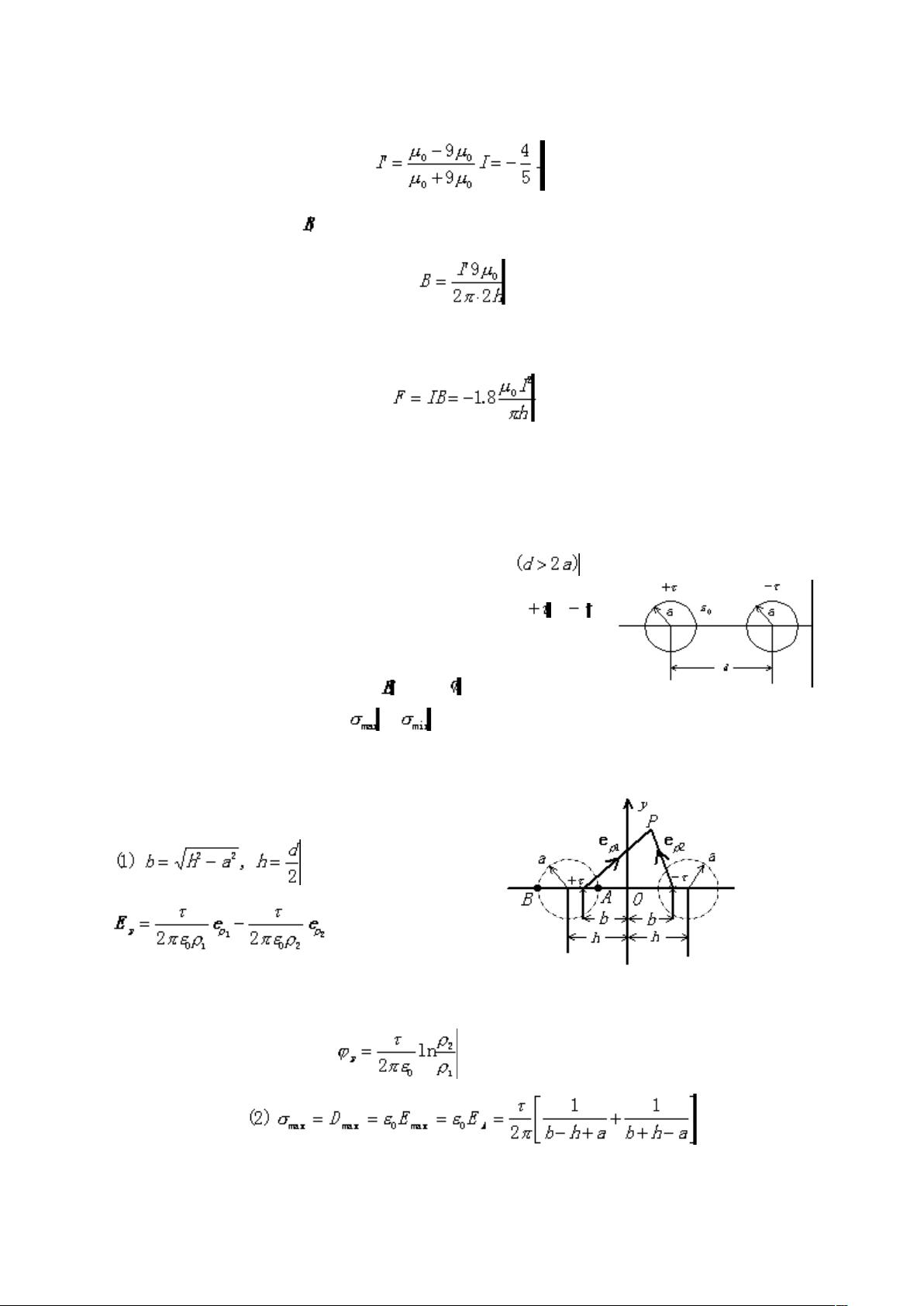
电磁场与电磁波是物理学中的核心领域，主要研究电场和磁场的性质、传播以及它们相互间的相互作用。大学电磁场与电磁波课程的试题涉及多个关键知识点，包括麦克斯韦方程组、电磁场边界条件、矢量位与规范、通量和散度、矢量场的特性、电流连续性方程、电偶极子的运动、以及静电场的基本理论。 1. 麦克斯韦方程组是电磁学的基础，它在非限定情况下以微分形式表示为：[pic]，这些方程揭示了电磁场与电荷和电流的关系，其中变化的电场产生磁场，变化的磁场产生位移电流，这是电磁波存在的理论基础。这四个方程共同表达了电磁场的动态行为，以及它们的源（如真实电流和位移电流）。 2. 时变电磁场在理想导体和理想介质界面的边界条件包括：[pic]，表示电流密度在界面上的连续性；[pic]，反映了磁场垂直于界面的条件；[pic]和[pic]则分别对应电场和磁场的法向分量在界面上的匹配。 3. 矢量位和动态矢量位在电磁场中的表达式分别为：[pic]和[pic]或[pic]，库仑规范和洛仑兹规范确保了电场和磁场的散度有唯一解，前者适用于静态场，后者适用于时变场，它们都限制了散度的发散性。 4. 穿过闭合曲面的通量是矢量场的重要概念，它描述了场线穿过表面的量。通量正负号代表了源的性质：正通量表示源向外扩散，负通量表示源向内汇聚，零通量表示无源。 5. 散度是矢量场的重要性质，例如，位置矢量的散度证明表明，散度值与坐标系选择无关，因为不同的坐标系统下计算结果一致。 6. 亥姆霍兹定理强调了矢量场的性质可以通过其散度和旋度来分析。例如，在静电场中，电场既有源又有旋，而在某些特定条件下，如静电场，散度为零而旋度不为零，意味着它是有源无旋的。 7. 当涉及到电流连续性，一般电流遵循积分形式：[pic]，而恒定电流则是[pic]。这描述了电流在空间中的分布和传输。 8. 电偶极子在电场中的运动取决于电场的均匀程度：在匀强电场中，电偶极子仅发生转动；在非匀强电场中，电偶极子不仅转动，还受到沿电场强度方向的平动。 9. 静电场的基本方程，无论是积分形式还是微分形式，都是描述电场如何由电荷分布决定的关键方程，对于理解电荷间相互作用至关重要。 通过解答这些问题，学生可以深入理解电磁场的基本原理，掌握相关理论和应用，从而在实际问题中运用所学知识。