W. He et al. / Information Sciences 380 (2017) 145–158 147
where x
i
(t) ∈ R
n
denotes the state of the i th node, f (x
i
(t)) = ( f
1
(x
i
(t)) , f
2
(x
i
(t)) , . . . , f
n
( x
i
( t)))
T
is a nonlinear function, u
i
(t)
is the control input, and A and B are constant matrices.
The leader’s dynamics is expressed as
˙
s (t) = As (t) + Bf (s (t)) (2)
The objective is to design a distributed networked-based impulsive controller u
i
(t) with only sampled data of the agent
and its neighbors at discrete instants such that all agents (1) reach global exponential consensus under the guidance of the
leader (2) .
Definition 1. The multi-agent system (1) is said to achieve global exponential consensus with the leader s (t) if there exist
two positive constants θ and ε such that for any x
i
(t
0
) , s (t
0
) ∈ R
n
x
i
(t) − s (t) ≤ θ x
i
(t
0
) − s (t
0
) e
−ε(t−t
0
)
, i = 1 , 2 , . . . , N
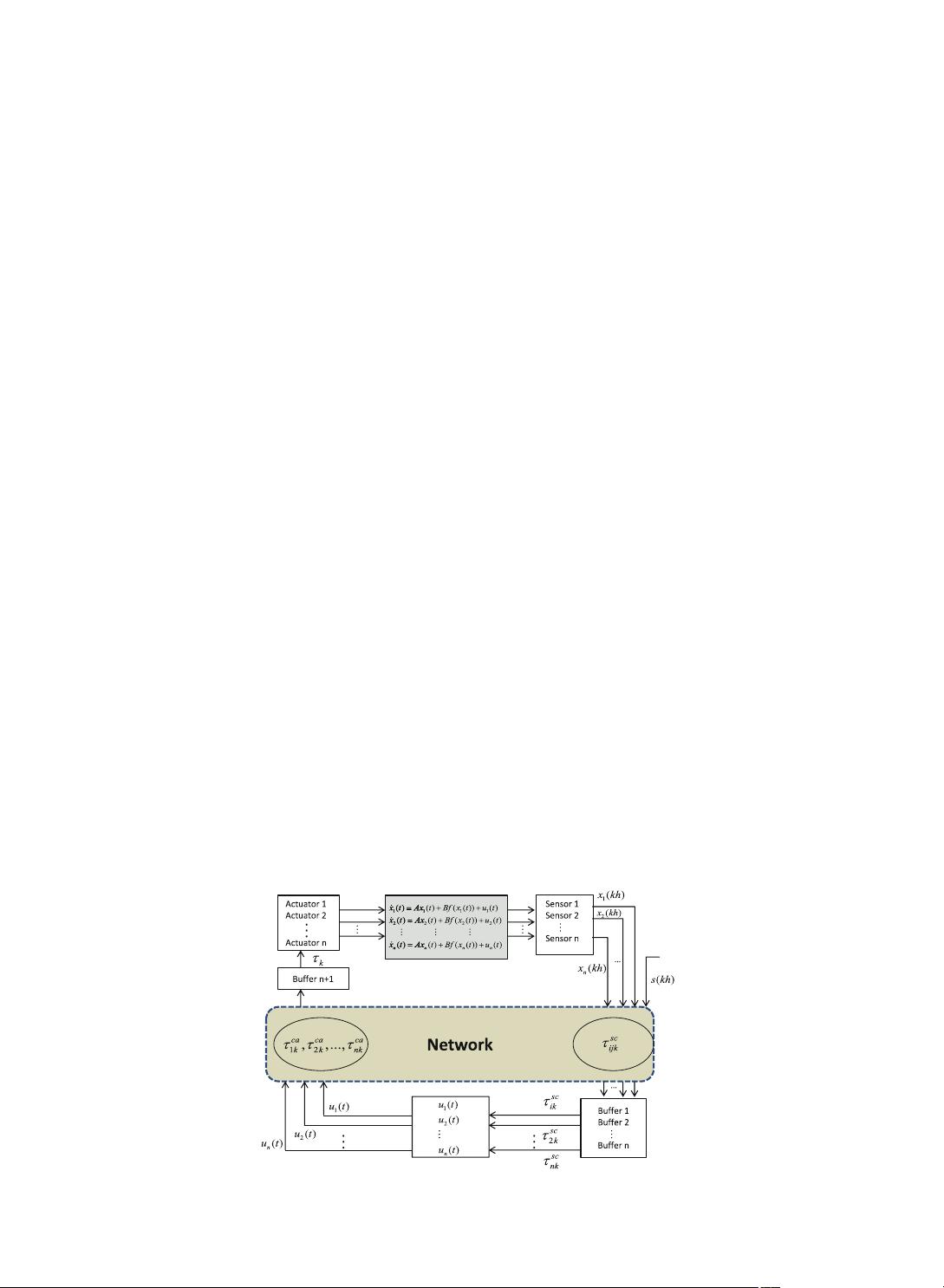
In this paper, a network-based control configuration is established, as shown in Fig. 1 , where sensor/actuator and an
impulsive controller of each agent are remotely distributed and connected via a communication network. It is assumed that
the sensor is clock-driven and both the controller and the buffers are event-driven. h is the sampling period. At t = t
0
+ kh ,
each agent’s information is sampled and transferred to its controller and other agents via a communication network. Buffer
i is used to store received information until all the data for the controller u
i
is collected. Let τ
sc
ijk
, i = 1 , . . . , N , j = 1 , . . . , N + 1
be the communication delay between the sensor j and Buffer i , where j = N + 1 denotes the sensor of the leader. Thus,
the time from the instant t
0
+ kh when sensor i samples data from agent i to the instant when the controller i is ready
is τ
sc
ik
= max { τ
sc
ijk
| i = 1 , . . . , N , j = 1 , . . . , N + 1 } . As the controller of each agent may arrive at the actuator at different time, a
common buffer n + 1 is employed to store all the controllers’ information to make all actuators operate at the same time.
Let τ
ca
ik
, i = 1 , . . . , N denote the delay from the controller i to Buffer n + 1 . Thus the total delay from the sensor to the actuator
for each agent can be defined as τ
k
= max { τ
sc
ik
+ τ
ca
ik
, i = 1 , . . . , N} . Then, a networked-based impulsive controller is designed
as
u
i
(t) =
∞
k =1
−c
N
j=1
l
ij
x
j
(t
0
+ kh ) − cd
i
(x
i
(t
0
+ kh ) − s (t
0
+ kh ))
δ(t − t
k
) (3)
where t
k
= t
0
+ kh + τ
k
, τ
min
= min
k
{ τ
k
| k ∈ N } , τ
max
= max
k
{ τ
k
| k ∈ N } , c is the coupling strength, and d
i
≥ 0 , i = 1 , 2 , . . . , N,
are pinning gains. Here, d
i
> 0 if and only if the i th node is informed by the leader. The node i is referred to as the pinned
node or controlled node, δ(·) is the Dirac impulse.
The design of a distributed networked-based impulsive controller u
i
(t) is related to the design of an impulse sequence
{ t
k
| k = 0 , 1 , . . . } and appropriate coupling strength c , pinning strategies d
i
, regarded as impulsive gains. As the impulse se-
quence t
k
= t
0
+ kh + τ
k
. Therefore, the design problem is turned to find appropriate sampling periods h , coupling strength
c and pinning strategies d
i
by taking transmittal delay τ
k
into account.
Define the error state e
i
(t) = x
i
(t) − s (t) . From (1)–(3) , we have the following error system:
⎧
⎪
⎨
⎪
⎩
˙
e
i
(t) = Ae
i
(t) + Bg (e
i
(t ) , s (t )) , t ∈ [ t
k −1
, t
k
)
e
i
(t
k
) − e
i
(t
−
k
) = −c
N
j=1
l
ij
e
j
( (t
k
− τ
k
)
−
) − cd
i
e
i
( (t
k
− τ
k
)
−
)
(4)
Fig. 1. Network-based control configuration for multi-agent system (1) .









