1062 IEEE TRANSACTIONS ON NEURAL NETWORKS AND LEARNING SYSTEMS, VOL. 26, NO. 5, MAY 2015
learned discriminative appearance models for each target to
distinguish between interaction targets. In order to achieve
robust tracking with unreliable detection source, a number
of particle filter-based methods avoid directly using the final
sparse detection output for computing the weights of the
particles. Breitenstein et al. [1] explored to use the continuous
detection confidence as a graded observation model to track
multiple persons. Their approach is based on a combination
of a class-specific pedestrian detector to localize people and
a particle filter to predict the target locations, incorporating
a motion model.
C. Detection Postprocessing
Existing detectors give repeated responses for a single
object, so postprocessing is needed to reconcile the multiple
responses, which is usually implemented by NMS.
Desai et al. [37] proposed a discriminative model to
learn the spatial interaction between different classes of
objects. The model learns statistics that capture spatial
arrangements of various object classes. Alternatively,
Sadeghi and Farhadi [38] decoded detector outputs to produce
final results through designing context-aware feature. They
argued that their feature representation resulted in a fast
and exact inference method. These methods used only static
information to construct their models. To the best of our
knowledge, there is no existing method that systematically
and schematically integrates temporal continuity and
scene structure in videos to conduct the reconciliation
postprocessing.
III. T
RACKING FRAMEWORK
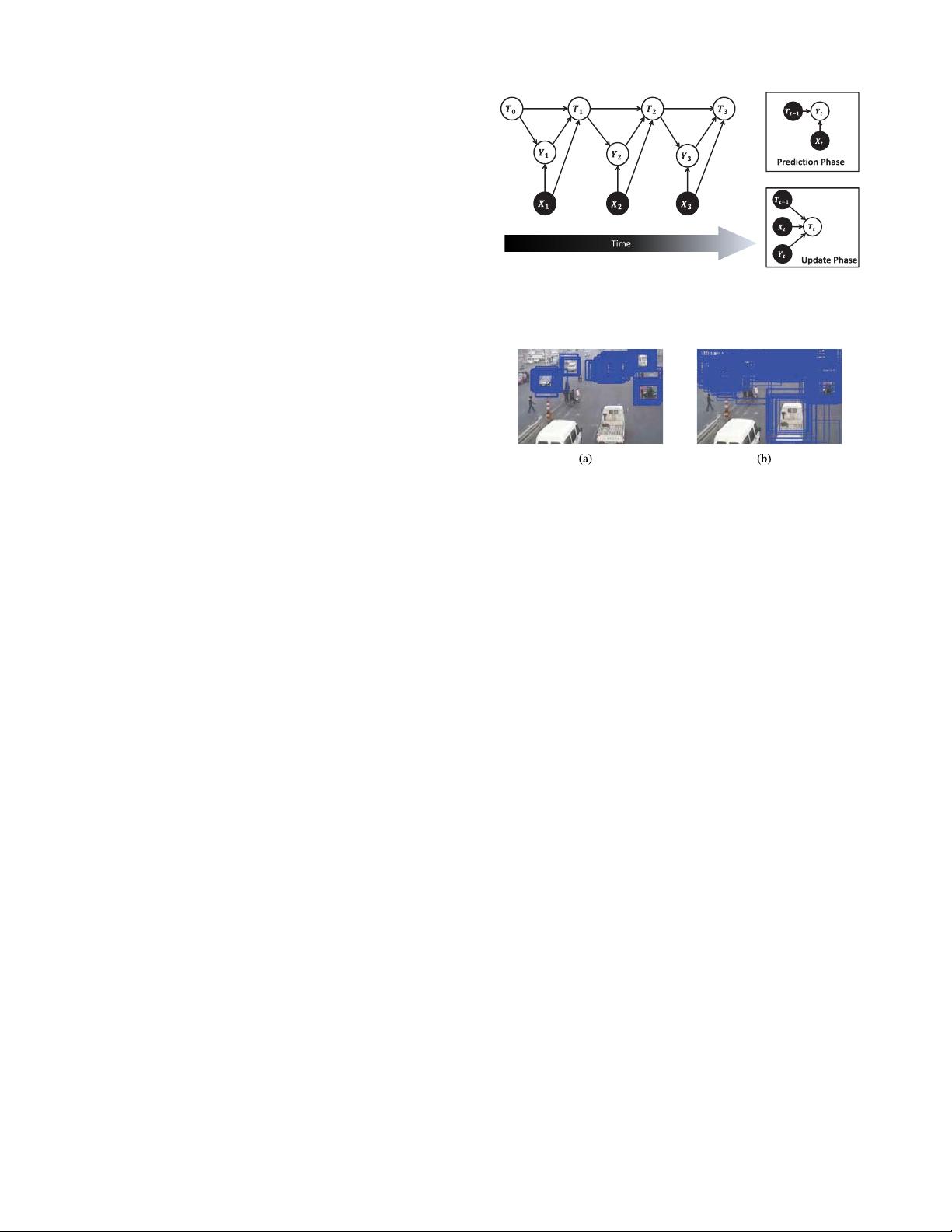
Our algorithm consists of two phases at each time step:
1) prediction and 2) update. At the prediction phase, the
algorithm predicts the labels of the observation based on the
previous tracking state. We use the original detection results
as observation. Some of these results correspond to existing
and newly tracked objects, but there are also repeated detec-
tions and FPs. The prediction operation is therefore required
to distinguish the observation data. Since the output labels
are interdependent, this is a structured prediction problem.
To achieve the necessary robustness, we learn a discriminative
max-margin model from training instead of heuristically defin-
ing a labeling strategy. Given the observation and previous
state as input, the model predicts the observation labels by
maximizing a potential function. At the update phase, the
algorithm uses labeled observation to update the tracking state.
We model the update phase in a first-order Markov chain, i.e.,
the current tracking state only relies on the state of the last
frame and the current observation. Fig. 1 shows the processing
line of our tracking framework.
A. Problem Setting and Notation
We use original detection results as observation. Instead of
proposing a new domain specific detection model, we simply
utilize the code of commonly used part-based model [24].
It should be mentioned that we only need root bounding boxes
Fig. 1. Our tracking processing line. It contains prediction phase and update
phase at each time step. At the prediction phase, the algorithm predicts labels
of the observation. At the update phase, the algorithm updates the tracking
states.
Fig. 2. (a) Threshold 0 is used and only 4/10 objects are successfully detected.
(b) Threshold −0.5 is used and 9/10 objects are successfully detected.
as observation for the following steps. Any other detector
which can return bounding boxes as the detection results is
suitable to take its place. This is a significant advantage over
other methods [4], which need a limb detector or body part
detector. To detect objects in an image, the local detector
evaluates the grid in each position, and each scale, by a filter-
like classifier and returns a detection score. A grid with a
higher score than a threshold will be regarded as a positive
response. Fig. 2(a) and (b) shows the detection responses with
different thresholds.
We collect the detection results above a relatively low
threshold so that all the targets that appear can be observed
most of the time. Each detection response at time t is then
represented as a 5-tube vector
X
i,t
=
x
i,t
, y
i,t
, s
(X)
i,t
, F
i,t
, r
i,t
(1)
where (x
i,t
, y
i,t
) indicates the center position of the detected
bounding box, s
(X)
i,t
indicates the area of the bounding box,
F
i,t
is the appearance descriptor, and r
i,t
is the detection score.
Suppose there are M detection results in total at time t.The
observation is represented by
X
t
={X
i,t
: i = 1 ...M}. (2)
Each tracked object is independently represented as a 6-tube
vector
T
i,t
=
u
i,t
,v
i,t
, ˙u
i,t
, ˙v
i,t
, s
(T )
i,t
, G
i,t
(3)
where (u
i,t
,v
i,t
) indicates its current center position, ( ˙u
i,t
, ˙v
i,t
)
indicates its velocity, s
(T )
i,t
is the area of the bounding box,
and G
i,t
is its appearance descriptor. Suppose there are K
activating trajectories at time t. The joint state is represented as
T
t
={T
i,t
: i = 1 ...K }. (4)
T
0
is initialized to be an empty set.









