大学生数值分析实验：复化算法求积分精度探究

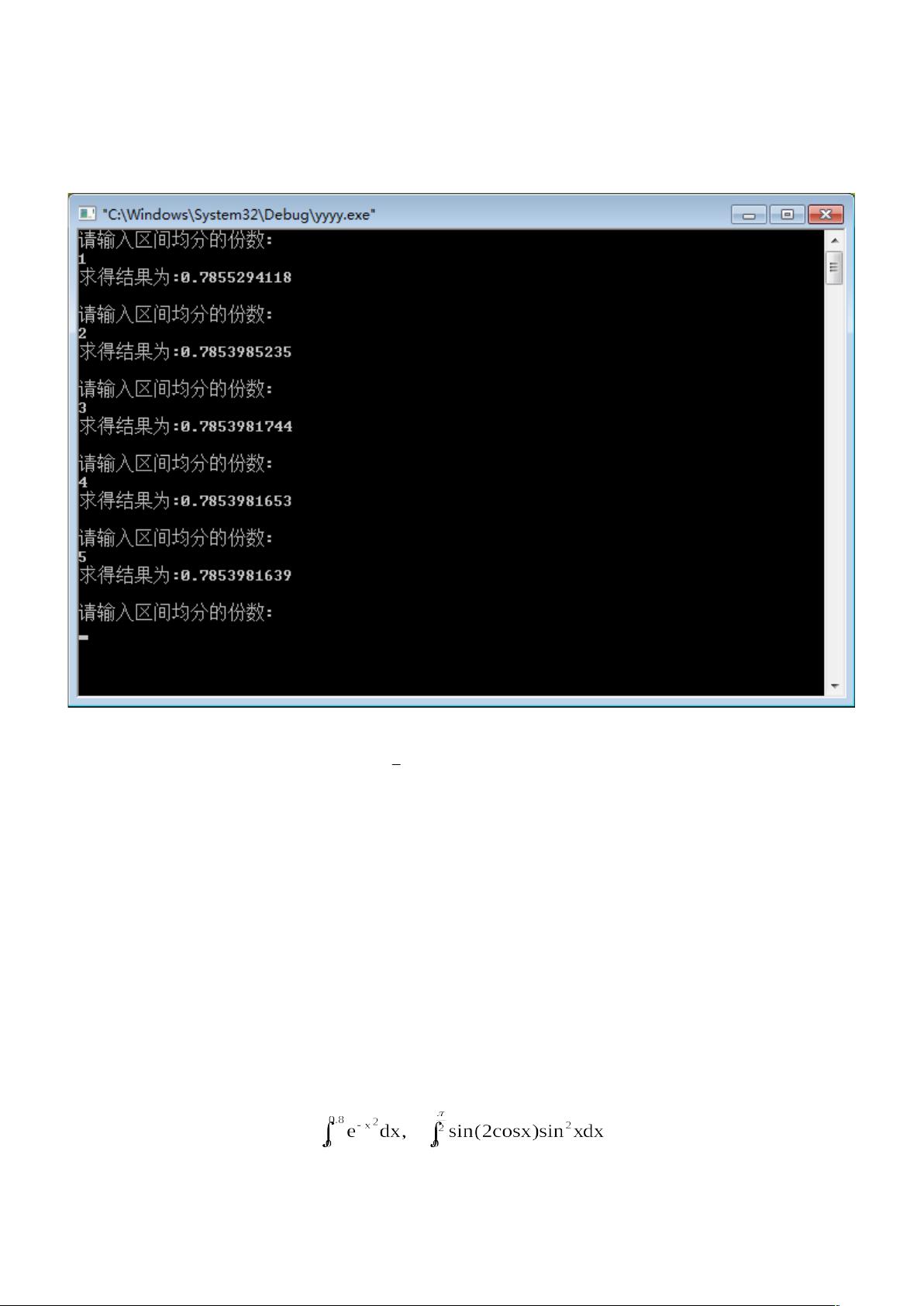
本资源是一份针对大学生设计的数值分析实验，旨在帮助他们理解和掌握数值积分方法。实验主要关注三个部分：数值积分方法的精确度体验、复化柯特斯求积公式的实现及其应用以及复化辛卜生法、龙贝格法和柯特斯算法的实际计算。 首先，实验的核心目的是让学生通过实际计算来体会数值积分方法的精度，比如复化辛卜生法和龙贝格法。这两个方法在数值分析中是重要的求积手段，它们能够有效地逼近连续函数的定积分，通过比较不同算法的结果，学生可以理解每种方法的优势和局限性。 实验内容分为两部分： 1. 实际计算复化柯特斯求积法：学生需要编写一个C++程序，利用循环结构实现柯特斯公式，该公式用于计算给定区间上的定积分。程序接收用户输入的区间均分份数n，然后通过多次迭代计算各个部分的贡献，并根据柯特斯公式汇总结果。程序运行结果显示，当n=2时，计算结果已经精确到小数点后六位，这说明随着细分程度的提高，数值积分的精度显著提升。 2. 复化辛普生、龙贝格和柯特斯算法的综合应用：接下来，实验引导学生运用复化辛普生算法和复化龙贝格算法进行同样的积分计算，这两种方法通常比单次柯特斯方法具有更高的精度。实验可能还涉及到比较三种方法在不同n值下的性能差异，以此来展示这些算法的适用场景和优化策略。 通过这些实验，学生不仅能够掌握数值积分的基本原理，还能通过实践操作提升编程技能，理解算法的效率和误差控制，从而加深对数值分析理论的理解和应用能力。同时，这种实验形式有助于培养学生的独立思考和问题解决能力，为他们在实际工程问题中的数值计算打下坚实的基础。